Теорема Гудстейна
|
Read other articles:

Damselfly Capung jarum ekor biru betina (Ischnura heterosticta) Klasifikasi ilmiah Kerajaan: Animalia Filum: Arthropoda Kelas: Insecta Ordo: Odonata Subordo: ZygopteraEdmond de Selys Longschamps, 1854 Families Amphipterygidae Calopterygidae Chlorocyphidae Coenagrionidae Dicteriadidae Diphlebiidae Euphaeidae Hemiphlebiidae Isostictidae Lestidae Lestoideidae Megapodagrionidae Perilestidae Platycnemididae Platystictidae Polythoridae Protoneuridae Pseudostigmatidae Synlestidae †Zacallitidae Ca...
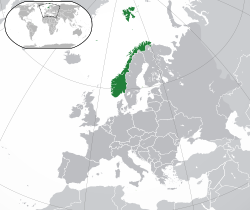
Country in Northern Europe This article is about the European country. For other uses, see Norway (disambiguation). Kingdom of Norway Other official names Kongeriket Norge (Bokmål)Kongeriket Noreg (Nynorsk)Norgga gonagasriika (Northern Sami)Vuona gånågisrijkka (Lule Sami)Nöörjen gånkarïjhke (Southern Sami)Norjan kuninkhaanvaltakunta (Kven) Flag Coat of arms Anthem: Ja, vi elsker dette landet(English: Yes, we love this country)Royal anthem: Konges...

Zyuganov beralih ke halaman ini. Untuk tokoh lain dengan marga tersebut, lihat Zyuganov (marga). Dalam nama yang mengikuti kebiasaan penamaan Slavia Timur ini, patronimiknya adalah Andreyevich. Gennady ZyuganovГеннадий Зюганов Ketua Dewan Pusat Persatuan Partai KomunisPetahanaMulai menjabat 22 Januari 2001 PendahuluOleg SheninPenggantiPetahanaSekretaris Tingkat Satu Komite Pusat Partai Komunis Federasi RusiaPetahanaMulai menjabat 14 Februari 1993 PendahuluValentin Kupts...

Railway station in Karnataka, India This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bhatkal railway station – news · newspapers · books · scholar · JSTOR (August 2016) (Learn how and when to remove this message) BhatkalExpress train and Passenger train stationGeneral informationLocationIndiaCoordinates13°59...

Building in Manhattan, New York This article is about the building in New York City. For other uses, see Sofia (disambiguation). The SofiaView from 61st Street and Columbus AvenueFormer namesKent Automatic Garage, Sofia Brothers WarehouseAlternative namesSofia ApartmentsGeneral informationTypeCondominiumArchitectural styleArt DecoAddress43 West 61st StreetTown or cityManhattan, New York CityCountryUnited StatesCoordinates40°46′14″N 73°59′00″W / 40.77056°N 73.98333�...

提示:此条目页的主题不是中國—瑞士關係。 關於中華民國與「瑞」字國家的外交關係,詳見中瑞關係 (消歧義)。 中華民國—瑞士關係 中華民國 瑞士 代表機構駐瑞士台北文化經濟代表團瑞士商務辦事處代表代表 黃偉峰 大使[註 1][4]處長 陶方婭[5]Mrs. Claudia Fontana Tobiassen 中華民國—瑞士關係(德語:Schweizerische–republik china Beziehungen、法�...

SMA Negeri 10 SurabayaInformasiDidirikan10 April 1977JenisSekolah NegeriAkreditasiA[1]Nomor Statistik Sekolah301056012010Nomor Pokok Sekolah Nasional20532243MaskotOctodistJumlah kelas33 Ruang KelasJurusan atau peminatanIPA dan IPSRentang kelasX MIPA dan X IPS XI MIPA dan XI IPS XII MIPA dan XII IPSKurikulumKurikulum 2013AlamatLokasiJl. Jemursari I No. 28, Surabaya, Jawa Timur, IndonesiaTel./Faks.(031) 8415273Situs websma10surabaya.sch.idLain-lainLulusanSatria Tama Hard...

حكومة القناصل الفرنسية 1799–1804معلومات عامةالبلد فرنسا — الجمهورية الفرنسية الأولى رئيس الحكومة نابليون بونابرت التكوين 9 نوفمبر 1799[1] النهاية 18 مايو 1804 المدة 4 سنواتٍ و6 أشهرٍ و9 أيامٍالمقر الرئيسي قصر التويليري حكومة المديرين الفرنسية 1795 ـ 1799 الإمبراطورية الفرنسية �...

German footballer (born 1961) Reinhard Stumpf Personal informationFull name Reinhard Karl Stumpf[1]Date of birth (1961-11-26) 26 November 1961 (age 62)Place of birth Lieblos, West GermanyHeight 1.91 m (6 ft 3 in)Position(s) Centre-backYouth career SpVgg DietesheimSenior career*Years Team Apps (Gls)1984–1985 Kickers Offenbach 21 (0)1985–1986 Karlsruher SC 9 (1)1986–1989 Kickers Offenbach 63 (2)1989–1992 1. FC Kaiserslautern 65 (1)1992–1994 Galatasaray 44 (...

GimNama lainLaverJenisRumput laut panganTempat asalKoreaMasakan nasional terkaitKorean cuisineBahan utamaAlga merahHidangan serupaNoriSunting kotak info • L • BBantuan penggunaan templat ini Media: Gim Nama KoreaHangul김 Alih AksaragimMcCune–ReischauerkimIPA[kim] Gim (김), juga diromanisasikan menjadi kim,[1] adalah nama Korea untuk spesies rumput laut pangan dalam genera Pyropia dan Porphyra, yang meliputi P. tenera, P. yezoensis, P. suborbiculata, P....

Административное деление Словении Топонимия Словении — совокупность географических названий, включающая наименования природных и культурных объектов на территории Словении. Структура и состав топонимии страны обусловлены её географическим положением, этнически�...

Men's 20 kilometres walk at the 2018 European Athletics ChampionshipsVenueOlympic StadiumLocationBerlinDates11 August 2018Competitors28 from 15 nationsWinning time1:20:42Medalists Álvaro Martín Spain Diego García Spain Vasiliy Mizinov Authorised Neutral Athletes← 20142022 → 2018 EuropeanAthletics ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 ...

61st season of the UEFA club football tournament 2015–16 UEFA Champions LeagueThe San Siro in Milan hosted the finalTournament detailsDatesQualifying:30 June – 26 August 2015Competition proper:15 September 2015 – 28 May 2016TeamsCompetition proper: 32Total: 78 (from 53 associations)Final positionsChampions Real Madrid (11th title)Runners-up Atlético MadridTournament statisticsMatches played125Goals scored347 (2.78 per match)Attendance5,114,427 (40,915 per match)Top ...

Bakso babi Semangkuk sup bakso babi Hanzi tradisional: 貢丸 Hanzi sederhana: 贡丸 Makna harfiah: pounded balls Alih aksara Mandarin - Hanyu Pinyin: gòngwán Min Nan - Romanisasi POJ: kòng-ôan nama alternatif Hanzi tradisional: 摃丸 Hanzi sederhana: 扛丸 Alih aksara Mandarin - Hanyu Pinyin: n/a Min - Romanisasi Min-nan : kòng-ôan Bakso babi adalah bakso Tiongkok yang terbuat dari daging babi Bakso babi umumnya adalah masakan Taiwan, China, Hong Kong dan wilayah Asia lainnya,...

American politician Rees Griffith Richardscirca 191216th Lieutenant Governor of OhioIn officeJanuary 9, 1882 – January 14, 1884GovernorCharles FosterPreceded byAndrew HickenlooperSucceeded byJohn G. WarwickMember of the Ohio Senatefrom the 22nd districtIn officeJanuary 7, 1878 – January 1, 1882Preceded byJ. K. RukenbrodSucceeded byJ. M. DickinsonMember of the Ohio House of Representativesfrom the Jefferson County districtIn officeJanuary 5, 1874 –&...

For other uses, see Spring (disambiguation). Commune in Alba, RomaniaȘpringCommuneChurch in ȘpringLocation in Alba CountyȘpringLocation in RomaniaCoordinates: 45°58′N 23°47′E / 45.967°N 23.783°E / 45.967; 23.783CountryRomaniaCountyAlbaGovernment • Mayor (2020–2024) Iulia Stănilă (PNL)Area91.13 km2 (35.19 sq mi)Elevation310 m (1,020 ft)Population (2021-12-01)[1]2,354 • Density26/km2 (67/sq&...

この項目では、男子代表について説明しています。女子代表については「サッカーバーレーン女子代表」をご覧ください。 サッカーバーレーン代表 国または地域 バーレーン協会 バーレーンサッカー協会愛称 The Red監督 フアン・アントニオ・ピッツィ最多出場選手 サルマーン・イーサ(156試合)最多得点選手 イスマイール・アブドゥラティフ(47得点) ホームカラー ...

American baseball player (born 1984) This article is about the American baseball player. For the American wrestler, see Ricky Romero (wrestler). Baseball player Ricky RomeroRomero with the Toronto Blue Jays in 2011PitcherBorn: (1984-11-06) November 6, 1984 (age 39)East Los Angeles, California, U.S.Batted: RightThrew: LeftMLB debutApril 9, 2009, for the Toronto Blue JaysLast MLB appearanceSeptember 25, 2013, for the Toronto Blue JaysMLB statisticsWin–loss r...

前橋都市圏 都市雇用圏 前橋都市圏 北緯36度23分 東経139度4分 / 北緯36.383度 東経139.067度 / 36.383; 139.067国 日本都道府県 群馬県中心都市 前橋市 高崎市 面積(2011)[1] • 合計 2,652.80 km2人口(2015)[2] • 合計 1,263,034人 • 密度 480人/km2域内総生産 (2010)[1] - 名目 5兆2516億円 前橋都市圏(まえばしとしけん)は�...

埼玉純真短期大学 埼玉純真短期大学大学設置/創立 1983年学校種別 私立設置者 学校法人純真学園本部所在地 埼玉県羽生市下岩瀬430北緯36度9分43.15秒 東経139度31分35.53秒 / 北緯36.1619861度 東経139.5265361度 / 36.1619861; 139.5265361座標: 北緯36度9分43.15秒 東経139度31分35.53秒 / 北緯36.1619861度 東経139.5265361度 / 36.1619861; 139.5265361学部 こども学科[注...














