Телеграфные уравнения
|
Read other articles:

Questa voce sugli argomenti trattati e storia contemporanea è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Trattato di Vienna Confini del trattato 10 novembre 1859 ...

Dominic BrianLahir26 November 1996 (umur 27)Surabaya, IndonesiaPekerjaanPenulisKebangsaanIndonesiaPendidikanInternational Design SchoolOrang tuaGidion Hindarto dan Debora Intan TrisnaKerabatGabriela Galice (adik) Dominic Brian (lahir 26 November 1996) adalah seorang penulis naskah komik Indonesia.[1] Dia sebelumnya terkenal berhasil mencatatkan namanya 2 kali dalam buku rekor dunia Guinness World Records setelah berhasil menunjukkan kemampuannya mengingat 76 deret angka dala...

Questa voce o sezione sull'argomento edizioni di competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. C.N.D. 1994-1995Campionato Nazionale Dilettanti 1994-1995 Competizione Campionato Nazionale Dilettanti Sport Calcio Edizione 47ª Organizzatore Lega Nazionale Dilettanti -Comitato per ...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (August 2010) (Learn how and when to remove this template message) This article relies excessively on references...

Ordinariat Militer SlowakiaVojenský ordinariátKatolik Katedral St SebastianLambang Ordinariat Militer SlowakiaLokasiNegara SlowakiaDekanatVikariat Angkatan Bersenjata[1]Vikariat Kepolisian[2]Vikariat Kementerian Kehakiman[3]Koordinat48°11′45.3″N 17°8′35.1″E / 48.195917°N 17.143083°E / 48.195917; 17.143083StatistikLuas49.035 km2 (18.933 sq mi)Populasi- Total(per 2021)22738[4][5]Paroki43[6...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Second Iemma ministry90th Cabinet of New South WalesPremier Morris IemmaDate formed2 April 2007 (2007-04-02)Date dissolved5 September 2008 (2008-09-05)People and organisationsMonarchQueen Elizabeth IIGovernorMarie BashirDeputy PremierJohn WatkinsNo. of ministers20Member partyLaborStatus in legislatureLabor Majority GovernmentOpposition partyLiberal–National CoalitionOpposition leaderBarry O'FarrellHistoryElection(s)2007 New South Wales state electionPredecesso...

ملصق ألماني من عام 1935 يذكر: «السياسة العالمية - الثورة العالمية. الماسونية منظمة دولية مملوكة لليهود ولها هدف سياسي يتمثل في إقامة الهيمنة اليهودية من خلال ثورة عالمية». المؤامرة اليهودية الماسونية نظرية مؤامرة معادية للسامية ومناهضة للماسونية، تنطوي على تحالف سري مزعوم �...

ما شياو وي معلومات شخصية الميلاد ديسمبر 1959 (64 سنة) مواطنة الصين [1] (1 ) تولى المنصب19 مارس 2018 الحياة العملية المهنة سياسي الحزب الحزب الشيوعي الصيني تعديل مصدري - تعديل ما شياو وي (مواليد ديسمبر 1959) (بالصينية: 马晓伟) طبيب وسياسي صيني شغل منصب ال�...

For other uses of Mikasa, see Mikasa. Mikasa SportsMikasa headquarters in Nishi-kuCompany typeKabushiki Kaisha (share company)IndustrySports EquipmentPredecessorMasuda Rubber Industries, Myojyo Rubber Industrial Co.FoundedMay 1, 1917; 107 years ago (1917-05-01)FounderMasutaro MasudaHeadquartersHiroshima, Chūgoku, JapanKey peopleYuji Saeki (President)ProductsSports balls, accessoriesRevenue¥6.5 billion (2010) [1]Total assets¥120 million (2016)Number of employees139...

Species of butterfly Aphnaeus orcas Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Lycaenidae Genus: Aphnaeus Species: A. orcas Binomial name Aphnaeus orcas(Drury, 1782)[1] Synonyms Papilio orcas Drury, 1782 Aphnaeus guttatus Plötz, 1880 Aphnaeus hollandi Butler, 1902 Aphnaeus rattrayi Sharpe, 1904 Aphnaeus orcas var. heliodorus Schultze, 1916 Aphnaeus orcas f. overlaeti Berger, 1953 Aphnaeus orcas f. fo...

Palawan Indigenous peoples in a community meeting in 2017 Demographics ofthe Philippines Philippine Statistics Authority Census Religions Languages Ethnic groups Country of citizenship Filipinos Indigenous Mestizos vte Palawan, the largest province in the Philippines, is home to several Indigenous ethnolinguistic groups namely, the Kagayanen, Tagbanwa, Palawano, Taaw't Bato, Molbog, and Batak tribes.[1] They live in remote villages in the mountains and coastal areas.[1][2...

Constituency of the Madhya Pradesh legislative assembly in India DharampuriConstituency No. 200 for the Madhya Pradesh Legislative AssemblyConstituency detailsCountryIndiaRegionCentral IndiaStateMadhya PradeshDistrictDharLS constituencyDharEstablished1972ReservationSTMember of Legislative Assembly16th Madhya Pradesh Legislative AssemblyIncumbent Kalu Singh Thakur PartyBharatiya Janata Party Dharampuri is one of the 230 Vidhan Sabha (Legislative Assembly) constituencies of Madhya Pradesh state...
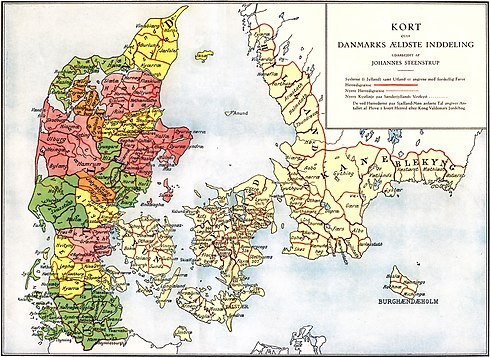
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Lands of Denmark – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Administrative division of Denmark in medieval times showing herreder and sysler. The entire country was divided into herreder, shown outlined in red. Colo...
У этого термина существуют и другие значения, см. Государство (значения). Титульный лист сочинения Томаса Гоббса «Левиафан» (1651 год), посвящённого проблемам государства Госуда́рство — политическая форма устройства общества на определённой территории, суверенная ф...

Video game engine id Tech 5Original author(s)John CarmackDeveloper(s)id SoftwareWritten inC++, AMPL, Clipper, Python (AI)PlatformMicrosoft Windows, OS X, PlayStation 3, PlayStation 4, Xbox 360, Xbox OnePredecessorid Tech 4Successorid Tech 6LicenseProprietaryWebsiteidsoftware.com id Tech 5 is a proprietary game engine developed by id Software. It followed its predecessors, id Tech 1, 2, 3 and 4, all of which had subsequently been published under the GNU General Public License. It was seen as a...

Federal Highway AdministrationHistoireFondation 1966CadreSigle (en) FHWAType Agence fédérale des États-UnisSiège WashingtonPays États-UnisOrganisationOrganisation mère Département des Transports des États-UnisSite web (en) highways.dot.govmodifier - modifier le code - modifier Wikidata La Federal Highway Administration (FHWA) est une agence du département des Transports des États-Unis responsable des autoroutes. Les principales activités de l'agence sont regroupées...

كأس السوبر الكويتي 2019 نادي الكويت نادي القادسية 0 1 التاريخ12 ديسمبر 2019 (2019-12-12)الملعبإستاد جابر الأحمد الدولي، العارضية، محافظة الفروانيةالحكمعبدالله الكندريالحضور5624 → 2018 2020 ← كأس السوبر الكويتي 2019 هي مُبارة بين بطل الدوري وبطل كأس الأمير نادي الكويت وبطل كأس ولي ...

Đối với các định nghĩa khác, xem Baltic. Bản đồ biển Baltic Biển Baltic (phiên âm: Ban-tích) hay còn gọi là Biển Đông (tiếng Đức: Ostsee) là biển rìa lục địa được bao bọc bởi bán đảo Scandinavia, khu vực Trung Âu và Đông Âu và quần đảo Đan Mạch. Biển Baltic nối với biển Trắng bởi kênh đào Biển Trắng và với Biển Bắc bởi kênh đào Kiel. Adam xứ Bremen (một sử gia người Đức) là ng...

Municipality in Rhineland-Palatinate, GermanyWallhausen Municipality Coat of armsLocation of Wallhausen within Bad Kreuznach district Wallhausen Show map of GermanyWallhausen Show map of Rhineland-PalatinateCoordinates: 49°53′17.48″N 7°45′56.16″E / 49.8881889°N 7.7656000°E / 49.8881889; 7.7656000CountryGermanyStateRhineland-PalatinateDistrictBad Kreuznach Municipal assoc.RüdesheimGovernment • Mayor (2019–24) Franz-Josef Jost[1] (C...






































