Схема Асмута — Блума
|
Read other articles:
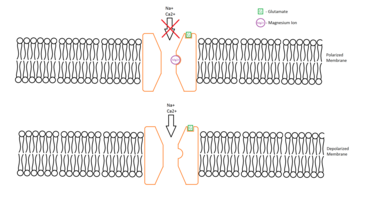
Glutametergic neuronal junction that is typically inactive In neuroscience, a silent synapse is an excitatory glutamatergic synapse whose postsynaptic membrane contains NMDA-type glutamate receptors but no AMPA-type glutamate receptors.[1] These synapses are named silent because normal AMPA receptor-mediated signaling is not present, rendering the synapse inactive under typical conditions. Silent synapses are typically considered to be immature glutamatergic synapses. As the brain mat...

British discount store chain The WorksCompany typePublicIndustryRetailFounded1981 (1981)HeadquartersColeshill, Warwickshire, England[1]Number of locations525 (stores)[2]Area servedUnited KingdomIrelandKey peopleDean Hoyle (Chairman)Gavin Peck (Group CEO)[3]ProductsBooks, stationery, arts, crafts and toysRevenue £264.6 million (2022)[4]OwnerDean Hoyle (15%)Websitetheworks.co.uk TheWorks.co.uk PLC, trading as The Works, is a discount retailer based in the U...

Wangsa Wettin adalah dinasti bangsawan yang selama lebih dari 800 tahun pernah menguasai dan memerintah wilayah yang sekarang menjadi negara bagian Sachsen, Jerman. Anggota dari wangsa ini juga selama beberapa waktu juga pernah menjadi penguasa Polandia. Jika dirunut lebih jauh, keturunan wangsa Wettin pada masa-masa yang berbeda pernah menduduki takhta Britania Raya, Portugal, Bulgaria, Polandia, Sachsen, dan Belgia. Dari semua negara-negara ini, hanya keturunan di Britania (dari cabang Sac...

Chronologie de la France ◄◄ 1714 1715 1716 1717 1718 1719 1720 1721 1722 ►► Chronologies Portrait de Louis XV, Jean Ranc, 1718.Données clés 1715 1716 1717 1718 1719 1720 1721Décennies :1680 1690 1700 1710 1720 1730 1740Siècles :XVIe XVIIe XVIIIe XIXe XXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature, Musique classique e...

聯合艦隊Rengo KantaiArmada Gabungan(Angkatan Laut Kekaisaran Jepang)Bendera Matahari TerbitAktif1894–1945NegaraKekaisaran JepangAliansi Kekaisaran JepangTipe unitKomponen laut Angkatan Laut Kekaisaran JepangPertempuranPerang Tiongkok-Jepang Pertama Perang Rusia-Jepang Perang Dunia IPerang Tiongkok-Jepang Kedua Perang Dunia IITokohTokoh berjasaIsoroku YamamotoTogo HeihachiroHiroyasu Fushimidan beberapa komandan lainnyaInsigniaTanda pengenalLambang Kekaisaran Jepang dan Lambang Angka...

José Leandro Andrade José Leandro Andrade nel 1926 circa Nazionalità Uruguay Altezza 180 cm Peso 79 kg Calcio Ruolo Centrocampista Termine carriera 1935 Carriera Squadre di club1 1921-1923 Bella Vista71 (17)1924-1930 Nacional180 (69)1931 Peñarol24 (6)1932-1933 River Plate (M)50 (11)1934 Atlanta18 (0)1935 Talleres (RdE)8 (3)1935 Peñarol10 (4) Nazionale 1923-1930 Uruguay34 (1) Palmarès Olimpiadi Oro Parigi 1924 Oro Amsterdam 1928 Mondi...

Jürgen Rohwer pada tahun 2004. Jürgen Rohwer (24 Mei 1924 – 24 Juli 2015) adalah seorang sejarawan militer angkatan laut Jerman dan emeritus profesor sejarah di Universitas Stuttgart, Jerman. Rohwer telah menulis lebih dari 400 buku dan esai tentang sejarah angkatan laut dan intelijen militer pada Perang Dunia II, yang mendapatkan pengakuan di seluruh dunia sebagai tokoh sejarawan dan otoritas terkemuka di U-boat.[1] Selama Perang Dunia II, antara tahun 1942 dan 1945...

2012 American filmJourney 2: The Mysterious IslandTheatrical release posterDirected byBrad PeytonScreenplay byBrian GunnMark GunnStory byRichard OuttenBrian GunnMark GunnBased onThe Mysterious Island1874 novelby Jules VerneProduced byBeau FlynnTripp VinsonCharlotte HugginsStarring Dwayne Johnson Michael Caine Josh Hutcherson Vanessa Hudgens Luis Guzmán Kristin Davis CinematographyDavid TattersallEdited byDavid RennieMusic byAndrew LockingtonProductioncompaniesNew Line CinemaWalden MediaCont...

2020 United States Supreme Court caseMcGirt v. OklahomaSupreme Court of the United StatesArgued May 11, 2020Decided July 9, 2020Full case nameJimcy McGirt, Petitioner, v. OklahomaDocket no.18-9526Citations591 U.S. ___ (more)140 S. Ct. 2452 207 L. Ed. 2d 985Case historyPriorDenial for relief, PC-2018-1057 (Okla. Crim. App. Feb. 25) (2019); Cert. granted, 140 S. Ct. 659 (2019)HoldingFor Major Crimes Act purposes, land reserved for the Creek Nation since the 19th century remains Indian country....

Schweiger nel 2022 Til Schweiger, all'anagrafe Tilman Valentin Schweiger (IPA: [ˈtɪlman ˈvaləntiːn ˈʃvaɪɡɐ]; Friburgo in Brisgovia, 19 dicembre 1963), è un attore, regista e produttore cinematografico tedesco. Indice 1 Biografia 2 Vita privata 3 Filmografia parziale 3.1 Attore 3.1.1 Cinema 3.1.2 Televisione 3.2 Regista 3.3 Sceneggiatore 3.4 Produttore 4 Doppiatori italiani 5 Altri progetti 6 Collegamenti esterni Biografia È noto soprattutto per aver interpretato Cynric nel film Ki...

Hari KanadaAnak-anak menonton pawai Hari Kanada di MontrealNama lainFête du Canada;sebelumnya bernama Hari DominionDirayakan olehBangsa Kanada (Kanada)JenisSejarah, kebudayaan, nasionalPerayaanKembang api, pawai, barbekyu, konser, karnival, pameran, piknikTanggal1 JuliFrekuensitahunan Pesta Kembang Api Hari Kanada di Quidi Vidi, St. John's, Newfoundland Hari Kanada (bahasa Prancis: Fête du Canada) adalah sebuah hari nasional di Kanada. Sebagai sebuah hari libur wajib federal, hari terse...

Lower extremity or limb of the human body (foot, lower leg, thigh and hip) This article is about the legs of humans. For the legs of other animals, see Leg. Human legLateral aspect of right legDetailsIdentifiersLatinmembrum inferiusFMA7184Anatomical terminology[edit on Wikidata] The leg is the entire lower limb of the human body, including the foot, thigh or sometimes even the hip or buttock region. The major bones of the leg are the femur (thigh bone), tibia (shin bone), and adjacent fib...

这是马来族人名,“莫哈末”是父名,不是姓氏,提及此人时应以其自身的名“马哈迪”为主。阿拉伯语“本”(bin)或“伊本”(ibn)、“宾蒂”(binti),意为后者是前者“某某之子”或“某某之女”。 尊敬的 敦马哈迪·莫哈末Mahathir bin Mohamad博士DK SMN SPMJ SSAP DGSM SPNS DUPN SPDK2018年的马哈迪馬來西亞第4、7任首相任期2018年5月10日—2020年3月1日辭職看守:2020年2月24日-2020�...

Senegalese footballer (born 1990) Magaye Gueye Gueye playing for Brest in 2013Personal informationFull name Magaye Serigne Falilou Dit Nelson Gueye[1]Date of birth (1990-07-06) 6 July 1990 (age 33)[2]Place of birth Nogent-sur-Marne, FranceHeight 1.83 m (6 ft 0 in)[2]Position(s) ForwardTeam informationCurrent team Anagennisi KarditsaNumber 29Youth career1999–2002 US Lognes2002–2008 StrasbourgSenior career*Years Team Apps (Gls)2008–2010 Strasbou...

Tiongkok Barat Tiongkok Barat (Hanzi sederhana: 中国西部; Hanzi tradisional: 中國西部; Pinyin: Zhōngguó Xībù; harfiah: 'Tiongkok Barat' atau yang sudah agak jarang disebut Hanzi sederhana: 华西; Hanzi tradisional: 華西; Pinyin: Huáxī; harfiah: 'Huaxia-Barat') adalah wilayah barat Republik Rakyat Tiongkok yang mencakup satu munisipal atau kota madya: Chongqing, enam provinsi: Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, dan Qinghai serta tiga daer...

Polish actress (born 1961) Danuta StenkaBorn (1961-10-10) 10 October 1961 (age 62)Sierakowice, PolandNationalityPolishOccupationActress Danuta Stenka (born 10 October 1961 in Sierakowice, Poland) is a Polish actress. She made her stage debut in 1984 and since then acted in many productions receiving theatre awards for her performances.[1] She made her big screen debut in 1995 and appeared in more than 60 movies since then. Stenka received two Polish Film Awards for Chopin: Desire...

For related races, see 1938 United States gubernatorial elections. 1938 Connecticut gubernatorial election ← 1936 November 8, 1938 1940 → Nominee Raymond E. Baldwin Wilbur Lucius Cross Jasper McLevy Party Republican Democratic Socialist Popular vote 230,237 227,549 166,253 Percentage 36.43% 36.00% 26.30% County results Municipality resultsMunicipal resultsBaldwin: 30–40% 40–50% ...

Амр ибн аль-Асараб. عمرو بن العاص Наместник Египта 661 — 664 Предшественник Мухаммад ибн Абу Бакр Личная информация Имя при рождении Амр ибн аль-Ас ибн Ваиль ибн Хашим ибн Саид ибн Сахм аль-Кураши Прозвище Абу Мухаммад, Абу Абдуллах Профессия, род деятельности полко...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 1931 French Championships – Men's singles – news · newspapers · books · scholar · JSTOR (March 2020) Men's singles1931 French ChampionshipsFinalChampion Jean Borotra[1]Runner-up Christian Boussus[1]Score2–6, 6–4, 7–5, 6–4Deta...
Seventh book of the Bible This article is about the biblical book. For other uses, see Judge (disambiguation). Judges in the Hebrew Bibleשופטים Italics indicate individuals not explicitly described as judges Book of Exodus Moses Book of Joshua Joshua Book of Judges Othniel Ehud Shamgar Deborah Gideon Abimelech Tola Jair Jephthah Ibzan Elon Abdon Samson First Book of Samuel Eli Samuel vte Hebrew Bible (Judaism) Torah (Instruction)GenesisBereshitExodusShemotLeviticusWayiqraNum...



































![{\displaystyle \mathbb {F} _{q}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16c2c0dbfb5f81ac9440269499abefe109f383bf)



![{\displaystyle s_{1}(X),s_{2}(X),\cdots ,s_{t}(X)\in \mathbb {F} _{q}[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3a1a5b598866785fed9fe83c98a042d30f3d062)










![{\displaystyle I^{B}={\mbox{HOK}}[I_{i},i\in B],\ M_{2}=\bigcap _{B\in \Gamma }RT(I^{B})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef996348ce5906f9c1c093cc1176a276d89ef4c6)



































