Регрессия (математика)
|
Read other articles:

Pertempuran Gerbang TrajanusBagian dari Peperangan Romawi Timur-BulgariaReruntuhan benteng Gerbang TrajanusTanggal17 Agustus 986LokasiTrayanovi Vrata, Bulgaria42°21′22″N 23°55′6″E / 42.35611°N 23.91833°E / 42.35611; 23.91833Koordinat: 42°21′22″N 23°55′6″E / 42.35611°N 23.91833°E / 42.35611; 23.91833Hasil Kemenangan menentukan BulgariaPihak terlibat Kekaisaran Bulgaria Pertama Kekaisaran Romawi TimurTokoh dan pemimpin Samu...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2017. AakatayiNama lainTeluguAakatayi SutradaraRom BhimanaProduserVijay Karan Kaushal Karan Anil Karan.SkenarioRom BhimanaCeritaRom BhimanaPemeranAashish Raj Bidkikar Rukshar Mir Brahmanandam Naveen NeniPenata musikMelody Brama Mani SharmaSinema...
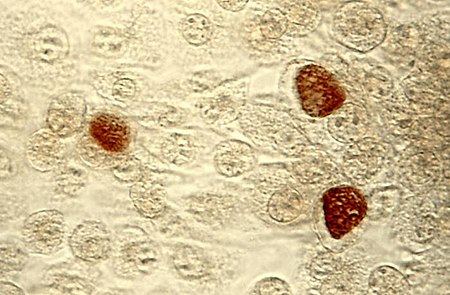
Untuk penyakit pada manusia, lihat Infeksi chlamydia. Chlamydia Badan inklusi C. trachomatis (coklat) pada kultur sel McCoy. Klasifikasi ilmiah Domain: Bakteri Filum: Chlamydiae Kelas: Chlamydiae Ordo: Chlamydiales Famili: Chlamydiaceae Genus: Chlamydia Spesies Chlamydia avium Sachse dkk. 2015[1] Chlamydia felis Sachse dkk. 2015[1] Chlamydia gallinacea Sachse dkk. 2015[1] Chlamydia muridarum Everett dkk. 1999Chlamydophila pecorum Fukushi & Hirai 1992, gen. nov. Eve...

Pertempuran PlasseyBagian dari Perang Tujuh TahunLord Clive meeting with Mir Jafar after the Battle of Plassey, oleh Francis Hayman (c. 1762)Tanggal23 Juni 1757LokasiPalashi, Benggala Barat, IndiaHasil Kemenangan East India CompanyPerubahanwilayah Benggala dianeksasi East India Company BritaniaPihak terlibat East India Company Subah Benggala French East India CompanyTokoh dan pemimpin Kolonel Robert CliveMajor KilpatrickMajor GrantMajor Eyre CooteCaptain Gaupp Nawab Bengal Siraj Ud DaulahMoha...

صابون حلبيالنوع صابون تعديل - تعديل مصدري - تعديل ويكي بيانات قطعة صابون حلبي الصابون الحلبي أو صابون الغار أو صابون رَگي[1] هو نوع من أنواع الصابون مُصنَّع من زيت الزيتون أو من زيوت نباتية أخرى وسمي كذلك لأن مدينة حلب في سوريا هي أقدم وأشهر المدن في صناعته.[2][3]&#...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Batasang Pambansa canvass for the 1986 Philippine presidential election – news · newspapers · books · scholar · JSTOR (July 2022) The following is the official canvassing of votes by the Batasang Pambansa for the 1986 Philippine presidential election....

Maurice AudinMaurice dan Josette AudinLahir(1932-02-14)14 Februari 1932Béja, TunisiaMeninggalsetelah 11 Juni 1957Warga negaraPrancisAlmamaterUniversitas AljazairKarier ilmiahPembimbing doktoralLaurent Schwartz Maurice Audin (14 Februari 1932 – setelah 11 Juni 1957) adalah seorang asisten matematikawan Prancis di Universitas ljazair, anggota Partai Komunis Aljazair dan penggiat antikolonialis, yang tewas saat disiksa oleh pihak Prancis pada Pertempuran Aljazair.[1] Selain universit...

Music award This article needs to be updated. Please help update this article to reflect recent events or newly available information. (February 2019) YouTube Music AwardsAwarded forBest in music videosCountryUnited StatesPresented byYouTubeFirst awardedNovember 3, 2013; 10 years ago (2013-11-03)Last awardedMarch 23, 2015; 9 years ago (2015-03-23)Website/YouTube/YTMA The YouTube Music Awards (commonly abbreviated as YTMA) was an awards show presented by the...

I. liga 1987-1988 Competizione I. liga Sport Calcio Edizione 81ª Organizzatore ČMFS Luogo Cecoslovacchia Partecipanti 16 Risultati Vincitore Sparta ČKD Praga(17º titolo) Retrocessioni Žilina Tatran Prešov Statistiche Miglior marcatore Milan Luhový (24) Incontri disputati 240 Gol segnati 715 (2,98 per incontro) Cronologia della competizione 1986-1987 1988-1989 Manuale L'edizione 1987/88 del campionato cecoslovacco di calcio vide la vittoria finale dello...
Security on property or debt For other uses, see Lien (disambiguation). Property law Part of the common law series Types Personal property Community property Real property Unowned property Acquisition Gift Adverse possession Deed Conquest Discovery Accession Lost, mislaid, and abandoned property Treasure trove Bailment License Alienation Estates in land Allodial title Fee simple Fee tail Life estate Defeasible estate Future interest remainder Concurrent estate Leasehold estate Condominiums Re...

Japanese rock band This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Flumpool – news · newspapers · books · scholar · JSTOR (July 2010) (Learn how and when to remove this message) flumpoolflumpool...

Disambiguazione – Se stai cercando altri significati, vedi Gilbert White (disambigua). Questa voce sugli argomenti scienziati britannici e ornitologi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Gilbert White Gilbert White (Selborne, 18 luglio 1720 – Selborne, 26 giugno 1793) è stato un naturalista e ornitologo britannico. Fra il 1768 e il 1793 collaborò con il naturalista William Markwick, osservando e catalogando più di 400 specie nell'Ham...

Aniello FalconeNaissance 15 novembre 1607NaplesDécès 14 juillet 1656 (à 48 ans)NaplesActivités Peintre, escrimeur ou escrimeuseLieu de travail Naples (1633-1656)modifier - modifier le code - modifier Wikidata Aniello Falcone, né le 15 novembre 1607 à Naples et mort le 14 juillet 1656 dans la même ville[1], est un peintre baroque italien de l'école napolitaine, contemporain de Diego Velázquez auquel il est comparé pour la puissance expressive de ses œuvres. Biographie Après un...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Malta Aviation Museum – news · newspapers · books · scholar · JSTOR (May 2016) (Learn how and when to remove this message) Malta Aviation MuseumMalta Aviation Museum entrance (2015)Established1994LocationTa'Qali, MaltaCoordinates35°53′37″N 14°24′58″E&...

Political convention of the Republican Party This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1980 Republican National Convention – news · newspapers · books · scholar · JSTOR (January 2009) (Learn how and when to remove this message) 1980 Republican National Convention1980 presidential election NomineesReaga...

Konten dan perspektif penulisan artikel ini tidak menggambarkan wawasan global pada subjeknya. Silakan bantu mengembangkan atau bicarakan artikel ini di halaman pembicaraannya, atau buat artikel baru, bila perlu. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini sudah memiliki referensi, tetapi tidak disertai kutipan yang cukup. Anda dapat membantu mengembangkan artikel ini dengan menambahkan lebih banyak kutipan pada teks artikel. (April 2009) (Pelajari cara dan...

American football player (born 1992) American football player Orleans DarkwaDarkwa with the New York Giants in 2017No. 32, 43, 26Position:Running backPersonal informationBorn: (1992-02-28) February 28, 1992 (age 32)Nashville, Tennessee, U.S.Height:5 ft 11 in (1.80 m)Weight:219 lb (99 kg)Career informationHigh school:The Ensworth School(Nashville, Tennessee)College:Tulane (2010–2013)Undrafted:2014Career history Miami Dolphins (2014) New York Giants (2014–2017)...

Arena in Queensland, Australia Carrara Indoor StadiumThe GreenhouseFormer namesCarrara Indoor Sports CentreLocationBroadbeach-Nerang Road, Carrara, QueenslandCoordinates28°0′20″S 153°21′55″E / 28.00556°S 153.36528°E / -28.00556; 153.36528OwnerGold Coast City CouncilOperatorGold Coast City CouncilCapacityBasketball: 2,992SurfaceSprung wooden floorTenantsGold Coast Rollers (NBL) (1990–1996)Squash Australia (Headquarters) (2018–) Carrara Indoor Stadium is ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) نظام فالانكس (CIWS) الصاروخي Phalanx CIWS إطلاق نظام فالانكس (CIWS) الصاروخي من حاملة الطائرات الأمريكيةإطلاق نظام ...

Mariamne IMariamne, raffigurata in un manoscritto miniato francese del XV/XVI secolo dell'opera di Giovanni Boccaccio De mulieribus clarisSovrana della GiudeaIn carica37 a.C.-29 a.C. SuccessoreMariamne II Morte29 a.C. Dinastiaasmonea ed erodiana PadreAlessandro Maccabeo MadreAlessandra Maccabeo ConsorteErode il Grande FigliAlessandro, Aristobulo, Salampsio, Cipro Mariamne (in greco antico: Μαριάμη?, Mariáme; ... – 29 a.C.) è stata una regina ebrea antica, seconda moglie di Er...







































