Разметка графа
|
Read other articles:

Halaman ini berisi artikel tentang tokoh. Untuk acara TV-nya, lihat The Ed Sullivan Show. Untuk penggunaan lainnya, lihat Edward Sullivan (disambiguasi). Ed SullivanSullivan pada tahun 1955LahirEdward Vincent Sullivan(1901-09-28)28 September 1901Harlem, New York City, ASMeninggal13 Oktober 1974(1974-10-13) (umur 73)Manhattan, New York City, New York, ASSebab meninggalKanker esofagealMakamFerncliff CemeteryPekerjaanPembawa acara televisi, wartawanTahun aktif1932–1974Suami/istr...

Andrea Barzagli Barzagli bermain untuk Italia pada 2012Informasi pribadiNama lengkap Andrea Barzagli[1]Tanggal lahir 8 Mei 1981 (umur 42)Tempat lahir Fiesole, ItaliaTinggi 187 cm (6 ft 2 in)[2]Posisi bermain Bek tengahKarier junior RondinellaKarier senior*Tahun Tim Tampil (Gol)1998–2000 Rondinella 51 (3)2000 Pistoiese 5 (0)2001 Rondinella 13 (1)2001–2003 Piacenza 0 (0)2001–2003 → Ascoli (pinjaman) 46 (3)2003–2004 Chievo 29 (3)2004–2008 Palermo ...

Ad AstraPoster film Ad AstraSutradaraJames GrayProduserBrad PittDede GardnerJeremy KleinerJames GrayRodrigo TeixeiraAnthony KatagasArnon MilchanDitulis olehJames GrayEthan GrossPemeranBrad PittTommy Lee JonesRuth NeggaLiv TylerDonald SutherlandPenata musikMax RichterLorne BalfeSinematograferHoyte van HoytemaPenyuntingJohn AxelradLee HaugenPerusahaanproduksiRegency EnterprisesBona Film GroupNew RegencyPlan B EntertainmentRT FeaturesKeep Your Head ProductionsMadRiver PicturesTSG Entertain...

العلاقات الإماراتية الإيطالية الإمارات العربية المتحدة إيطاليا الإمارات العربية المتحدة إيطاليا تعديل مصدري - تعديل العلاقات الإماراتية الإيطالية هي العلاقات الثنائية التي تجمع بين الإمارات العربية المتحدة وإيطاليا.[1][2][3][4][5] مقار...

العلاقات النرويجية الزيمبابوية النرويج زيمبابوي النرويج زيمبابوي تعديل مصدري - تعديل العلاقات النرويجية الزيمبابوية هي العلاقات الثنائية التي تجمع بين النرويج وزيمبابوي.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتي�...
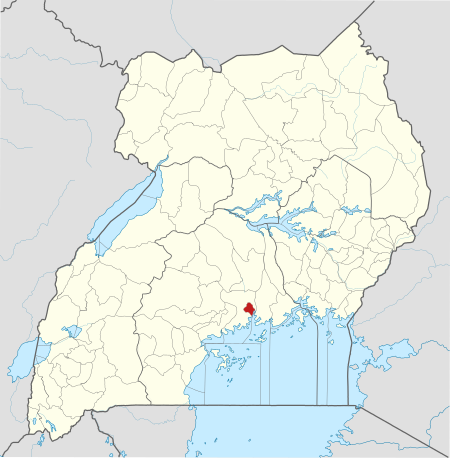
Hospital in Central Region, UgandaKiruddu General HospitalUganda Ministry of Health and Kampala Capital City AuthorityGeographyLocationSalaama, Kampala, Makindye Division, Central Region, UgandaCoordinates00°14′53″N 32°36′45″E / 0.24806°N 32.61250°E / 0.24806; 32.61250OrganisationCare systemPublicTypeGeneralServicesEmergency departmentIIIBeds200[1]HistoryOpened16 May 2016 [1]LinksOther linksHospitals in Uganda Kiruddu General Hospital, also...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2018) مقاطعة ويستون علم الإحداثيات 43°50′N 104°34′W / 43.84°N 104.56°W / 43...

Pour les articles homonymes, voir Toussaint (homonymie). Jean-Philippe Toussaint Jean-Philippe Toussaint, à Florence, en 2013. Données clés Naissance 29 novembre 1957 (66 ans) Bruxelles, Belgique Nationalité Belge Activité principale Romancier, réalisateur Formation Athénée Robert CatteauInstitut d'études politiques de Paris Distinctions Prix Victor Rossel (1997)Prix Médicis (2005) Prix Décembre (2009)membre de l'ARLLFB depuis 2014 Auteur Langue d’écriture français Œuvre...

1942 mystery film noir by Jack Conway For other uses, see Crossroads (disambiguation). CrossroadsTheatrical release posterDirected byJack ConwayScreenplay byGuy TrosperStory byJohn H. KafkaHoward Emmett RogersBased onthe screenplay of the film Crossroadsby John H. KafkaProduced byEdwin H. KnopfStarring William Powell Hedy Lamarr Claire Trevor Basil Rathbone CinematographyJoseph RuttenbergEdited byGeorge BoemlerMusic byBronislau KaperProductioncompanyMetro-Goldwyn-MayerDistributed byLoew's Inc...

American former professional basketball player Jason KaponoKapono with the Miami Heat in 2007Personal informationBorn (1981-02-04) February 4, 1981 (age 43)Long Beach, California, U.S.NationalityAmericanListed height6 ft 8 in (2.03 m)Listed weight215 lb (98 kg)Career informationHigh schoolArtesia (Lakewood, California)CollegeUCLA (1999–2003)NBA draft2003: 2nd round, 31st overall pickSelected by the Cleveland CavaliersPlaying career2003–2013PositionSmall forwa...

Barbie - La principessa e la poverafilm d'animazione direct-to-video La principessa Annalisa e la povera Erika in una scena del film Titolo orig.Barbie as the Princess and the Pauper Lingua orig.inglese PaeseStati Uniti d'America RegiaWilliam Lau ProduttoreJesyca C. Durchin, Jennifer Twiner McCarron SoggettoMark Twain SceneggiaturaCliff Ruby, Elana Lesser Dir. artisticaRob Jensen MusicheArnie Roth StudioMattel Entertainment, Mainframe Studios EditoreLions Gate Home Entertainme...

American popular music vocal group This article is about the band. For other uses, see Fifth Dimension (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2020) (Learn how and when to remove this message) The 5th DimensionThe 5th Dimension in 1969Back row: Townson and McLemore.Front row: LaRue, Davis, and McCoo.Background informationAlso k...

Il segreto di Vera Drakeuna scena del filmTitolo originaleVera Drake Paese di produzioneRegno Unito Anno2004 Durata125 min Generedrammatico RegiaMike Leigh SoggettoMike Leigh SceneggiaturaMike Leigh Distribuzione in italianoBiM Distribuzione FotografiaDick Pope MontaggioJim Clark MusicheAndrew Dickson ScenografiaJohn Bush CostumiJacqueline Durran Interpreti e personaggi Imelda Staunton: Vera Drake Phil Davis: Stan Peter Wight: ispettore Webster Adrian Scarborough: Frank Heather Craney: Joyce ...

Sébastien Pocognoli Pocognoli bermain untuk Belgia pada tahun 2008Informasi pribadiTanggal lahir 1 Agustus 1987 (umur 36)Tempat lahir Seraing, BelgiaTinggi 1,82 m (5 ft 11+1⁄2 in)[1]Posisi bermain BekInformasi klubKlub saat ini Brighton & Hove Albion(pinjaman dari West Bromwich Albion)Nomor 12Karier junior2000–2005 Standard LiègeKarier senior*Tahun Tim Tampil (Gol)2005–2007 Genk 45 (1)2007–2010 AZ Alkmaar 64 (5)2010–2013 Standard Liège 85 (2)2...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

تشين بينغ معلومات شخصية الميلاد 22 أكتوبر 1924 فيرق الوفاة 16 سبتمبر 2013 (88 سنة) بانكوك مواطنة ماليزيا عضو في جيش الشعب الماليزي المناهض لليابان [لغات أخرى]، وجيش التحرير الوطني المالايوي الحياة العملية المهنة سياسي، وبارتيزان الحزب الح�...

Terranova e Labradorprovincia(EN) Newfoundland and Labrador(FR) Terre-Neuve-et-Labrador (dettagli) (dettagli) Terranova e Labrador – VedutaSaint John's LocalizzazioneStato Canada AmministrazioneCapoluogoSaint John's Luogotenente GovernatoreJudy Foote dal 3 maggio 2018 Primo ministroAndrew Furey dal 19 agosto 2020 Lingue ufficialiInglese (de facto) Data di istituzione31 marzo 1949 TerritorioCoordinatedel capoluogo47°33′37.94″N 52°42′46.19″W47°33′37.94″N, 5...

Lesbian radical feminist advocacy group Part of a series onLesbian feminism Women's liberation movement People Paula Gunn Allen Dorothy Allison Ti-Grace Atkinson Alison Bechdel Evelyn Torton Beck Miriam Ben-Shalom Julie Bindel Ivy Bottini Charlotte Bunch Cheryl Clarke Michelle Cliff Kate Clinton Jeanne Córdova Mary Daly Max Dashu Stormé DeLarverie Diane DiMassa Alix Dobkin Andrea Dworkin Elana Dykewomon Lillian Faderman Ferron Marilyn Frye Michiyo Fukaya Carolyn Gage Donna Gottschalk Sarah ...

NgromboDesaKantor Desa NgromboPeta lokasi Desa NgromboNegara IndonesiaProvinsiJawa TengahKabupatenSukoharjoKecamatanBakiKode pos57556Kode Kemendagri33.11.10.2001 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Ngrombo adalah desa di kecamatan Baki, Sukoharjo, Jawa Tengah, Indonesia. Desa ini juga merupakan desa yang begitu dikenal luas oleh masyarakat Kota Solo dan sekitarnya, terutama dalam sentra produsen/Kerajinan Gitar, bahkan penjualannya pun tembus ke mancanegara. Pembagi...

Cyantraniliprole Names Preferred IUPAC name 4-Bromo-1-(3-chloropyridin-2-yl)-N-[4-cyano-2-methyl-6-(N-methylcarbamoyl)phenyl]-1H-pyrazole-5-carboxamide Other names Cyazypyr; Exirel Identifiers CAS Number 736994-63-1 Y 3D model (JSmol) Interactive image ChEBI CHEBI:132300 ChemSpider 9753377 ECHA InfoCard 100.205.162 PubChem CID 11578610 UNII LO6K6H48FD Y CompTox Dashboard (EPA) DTXSID2058174 InChI InChI=1S/C19H14BrClN6O2/c1-10-6-11(9-22)7-12(18(28)23-2)16(10)25-19(29)14-8-15(20)26-2...


