Парадокс Галилея
|
Read other articles:

This is a list of aircraft used by Portugal in World War II who never fought in World War II but from 1944 cooperated with the Allies in a non-belligerent capacity giving access to Portuguese territorial possessions for Allied forces. Most World War II Portuguese aircraft were confiscated from Allied forces. A number of Allied aircraft on their way to the North African campaign were forced to land in Portugal due to problems with the aircraft, after which they were confiscated by Portuguese ...

Robert PatrickPatrick di 2014 San Diego Comic-Con InternationalLahirRobert Hammond Patrick, Jr.5 November 1958 (umur 65)Marietta, Georgia, A.S.Pekerjaan Aktor Pengisian suara Tahun aktif1983–sekarangSuami/istriBarbara Patrick (m. 1990)Anak2 Robert Hammond Patrick Jr. (lahir 5 November 1958) adalah seorang aktor dan pengisi suara Amerika. Dikenal karena penggambaran karakter jahatnya,[1] Patrick adalah seorang Saturn Award pemenang dengan emp...

Tansu ÇillerÇiller di Brussel, Januari 1994 Perdana Menteri Turki ke-22PresidenSüleyman DemirelWakilMurat KarayalçınHikmet ÇetinDeniz BaykalPendahuluSüleyman DemirelPenggantiMesut YılmazWakil Perdana Menteri TurkiPerdana MenteriNecmettin ErbakanPendahuluNahit MenteşePenggantiİsmet SezginMenteri Urusan Luar NegeriPerdana MenteriNecmettin ErbakanPendahuluEmre GönensayPenggantiİsmet Cem Informasi pribadiLahirTansu Penbe24 Mei 1946 (umur 77)Istanbul, TurkiPartai politikPartai Jal...

2019 smartphone gameYou can help expand this article with text translated from the corresponding article in Japanese. (July 2020) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text in...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Railway station in Hampshire, England NetleyNetley station buildingGeneral informationLocationNetley, EastleighEnglandGrid referenceSU464085Managed bySouth Western RailwayPlatforms2Other informationStation codeNTLClassificationDfT category EHistoryOpened5 March 1866Original companySouthampton and Netley RailwayPre-groupingLondon and South Western RailwayPost-groupingSouthern RailwayPassengers2018/19 91,1302019/20 88,1082020/21 25,2922021/22 64,7642022/23 73,804 NotesPassenger statistics from ...

Alarik beralih ke halaman ini. Untuk kegunaan lain, lihat Alarik (disambiguasi).AlarikPotret imajiner AlarikRaja VisigothBerkuasa395–410Penobatan395PendahuluAtanarikPenerusAtaulfKelahiranc. 370Pulau PeukeKematian410KonsentiaPemakamanSungai BusentoWangsaBaltiAyahTidak diketahui[1]AgamaArianisme Alarik I (/ˈælərɪk/; Goth: 𐌰𐌻𐌰𐍂𐌴𐌹𐌺𐍃, Alarīks, penguasa semua;[2] c. 370 – 410 M) adalah raja pertama Visigoth, dari 395 hingga 410. Ia naik ke ...

إليوت لايك الإحداثيات 46°23′00″N 82°39′00″W / 46.383333333333°N 82.65°W / 46.383333333333; -82.65 [1] تاريخ التأسيس 1955 تقسيم إداري البلد كندا[2] خصائص جغرافية المساحة 714.65 كيلومتر مربع[3] عدد السكان عدد السكان 10741 (2016)[3] الكثافة السكانية 15.02 نسم...

Armenian television singing competition This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Voice of Armenia – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) The Voice of ArmeniaArmenianՀայաստանի ձայնըHayastani Dzayne GenreReality competitionCreated byJohn de MolJudges Nune Yesayan (2...

American university president (1899–1985) Milton S. Eisenhower8th and 10th President of Johns Hopkins UniversityIn office1971–1972Preceded byLincoln GordonSucceeded bySteven MullerIn office1956–1967Preceded byLowell ReedSucceeded byLincoln Gordon11th President of Pennsylvania State UniversityIn office1950–1956Preceded byJames Milholland (acting)Succeeded byEric A. Walker9th President of Kansas State UniversityIn office1943–1950Preceded byFrancis FarrellSucceeded byJames McCainDirect...
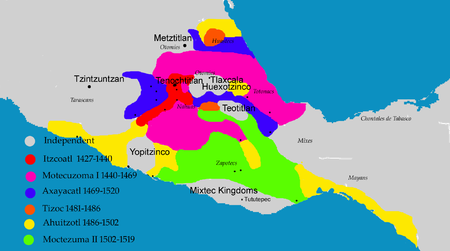
TizocTlatoani TenochtitlanTizoc di Codex Telleriano-RemensisBerkuasa1481–1486PendahuluAxayacatlPenerusAhuitzotlKematian1486AyahTezozomocIbuAtotoztli II Tizocic [ti'sosik] atau Tizocicatzin [tisosi'kat͡sin] (bentuk honorifik namanya), dalam bahasa Inggris disebut Tizoc, adalah tlatoani Tenochtitlan ketujuh. Biografi Keluarga Tizoc adalah putra dari Putri Atotoztli II dan sepupunya, pangeran Tezozomoc. Ia adalah cucu dari Raja Moctezuma I dan Itzcoatl. Raja Cuauhtototzin adalah nenek moyangn...

Mr. TrotNama alternatifTomorrow Is Mr. TrotHangul내일은 미스터트롯 PresenterKim Sung-jooLagu pembukaNest(Nam Jin)Lagu penutupNest(Nam Jin)Negara asalKorea SelatanBahasa asliKoreaJmlh. episode12ProduksiLokasi produksiKorea SelatanDurasi160 menitRumah produksiGolden Eight MediaDistributorTV ChosunRilis asliJaringanTV ChosunFormat gambarHDTV 1080iRilis2 Januari (2020-01-02) –12 Maret 2020 (2020-3-12) Mr. Trot (Hangul: 내일은 미스터트롯; lit. To...

Lying Is the Most Fun a Girl Can Have Without Taking Her Clothes OffLagu oleh Panic! at the Discodari album A Fever You Can't Sweat OutDirilis7 Agustus 2006FormatSingel CD, Vinyl 7Direkam2005SOMD! StudiosCollege Park, MarylandDang! StudiosLewisville, TexasGenrePop punk, electropunkDurasi3:20 (versi album)2:57 (versi radio)LabelDecaydance/Fueled by RamenPenciptaRyan Ross, Brendon Urie, Spencer SmithProduserMatt Squire Lying Is the Most Fun a Girl Can Have Without Taking Her Clothes Off atau se...

Roman emperor from 117 to 138 This article is about the Roman emperor. For other uses, see Hadrian (disambiguation). HadrianBust of Hadrian, c. 130Roman emperorReign11 August 117 – 10 July 138PredecessorTrajanSuccessorAntoninus PiusBornPublius Aelius Hadrianus24 January 76Italica, Hispania Baetica (present-day Santiponce, Spain)Died10 July 138 (aged 62)Baiae, ItaliaBurialPuteoliGardens of DomitiaHadrian's MausoleumSpouseVibia SabinaAdoptive childrenLucius Aelius CaesarAntoninus PiusRe...
Lic. Gustavo Díaz Ordaz International AirportAeropuerto Internacional de Puerto Vallarta Lic. Gustavo Díaz OrdazControl towerIATA: PVRICAO: MMPR PVRLocation of airport in MexicoInformasiJenisPublicPengelolaGrupo Aeroportuario del PacíficoMelayaniPuerto Vallarta and Riviera NayaritLokasiPuerto Vallarta, JaliscoKetinggian dpl7 mdplSitus webaeropuertosgap.com.mxLandasan pacu Arah Panjang Permukaan kaki m 04/22 10,171 3,100 Aspal Statistik (2011)Total Passengers2,535,900Source: Grupo...

Representation of 3D and 4D polytopes Examples colored by the number of sides on each face. Yellow triangles, red squares, and green pentagons. A tesseract projected into 3-space as a Schlegel diagram. There are 8 cubic cells visible: the outer cell into which the others are projected, one below each of the six exterior faces, and one in the center. Various visualizations of the icosahedron editperspectiveNetOrthogonal PetrieSchlegelVertex figure In geometry, a Schlegel diagram is a projectio...

Sports NightTitolo originaleSports Night PaeseStati Uniti d'America Anno1998-2000 Formatoserie TV Generecommedia drammatica Stagioni2 Episodi45 Durata22 min (episodio) Lingua originaleinglese Rapporto4:3 CreditiInterpreti e personaggi Peter Krause: Casey McCall Josh Charles: Dan Rydell Robert Guillaume: Isaac Jaffe Felicity Huffman: Dana Whitaker Joshua Malina: Jeremy Goodwin Sabrina Lloyd: Natalie Hurley Doppiatori e personaggi Andrea Ward: Casey McCall Mauro Gravina: Dan Rydell Carlo Marini...

10th-century Islamic scholar Abu Dharr al-HarawiTitleMuhaddith al HaramaynAl-ḤāfiẓPersonalBorn946 CE/355 AHHerat, (modern-day Afghanistan)Died1042 (aged 95–96)Mecca, (modern-day Hejaz)ReligionIslamEraIslamic golden ageDenominationSunniJurisprudenceMalikiCreedAsh'ari[1][2]Main interest(s)HadithOccupationMuhaddithMuslim leader Influenced by Malik Ibn AnasAbu Hasan al-Ash'ariAl-BaqillaniAl-KhattabiAl-DaraqutniAl-Hakim al-Nishapuri Part of a series onAsh'arism...

Two-manat the XXII Olympic Winter GamesDisqualified Russian teamDates16–17 FebruaryCompetitors60 from 20 nationsWinning time3:46.05Medalists Beat Hefti Alex Baumann Switzerland Steven Holcomb Steven Langton United States Oskars Melbārdis Daumants Dreiškens Latvia← 20102018 → The original podium. Bobsleigh at the2014 Winter OlympicsQualification TwomenwomenFourmenvte The two-man bobsleigh competition at the 2014 Winter Olympics in Sochi, R...

Mountain in Antarctica Mount AndersonMount Anderson Antarctica Highest pointElevation4,254 m (13,957 ft)[1]Prominence1,504 m (4,934 ft)[1]ListingUltras of AntarcticaCoordinates78°09′00″S 86°13′01″W / 78.15°S 86.217°W / -78.15; -86.217[2]GeographyLocation AntarcticaParent rangeSentinel Range,(Ellsworth Mountains)ClimbingFirst ascentJanuary 7th 2007 - Jed Brown (US) & Damien Gildea (AUS) Location ...
