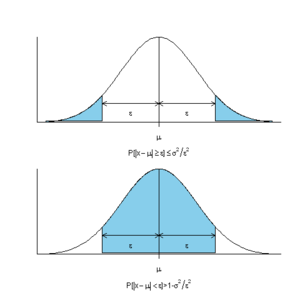
Неравенство Чебышёва
|
Read other articles:

Artikel ini memiliki beberapa masalah. Tolong bantu memperbaikinya atau diskusikan masalah-masalah ini di halaman pembicaraannya. (Pelajari bagaimana dan kapan saat yang tepat untuk menghapus templat pesan ini) Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Festivalist – berita&...

Freshwater lake in Kenya Lake NaivashaLake NaivashaCoordinates0°46′6.70″S 36°21′2.32″E / 0.7685278°S 36.3506444°E / -0.7685278; 36.3506444Basin countriesKenyaSurface area139 km2 (54 sq mi)Average depth6 m (20 ft)Max. depth30 m (98 ft)Surface elevation1,884 m (6,181 ft) Ramsar WetlandDesignated10 April 1995Reference no.724[1] Satellite image of Lake Naivasha Location of Naivasha in Kenya Lake Nai...

Gunung LakaanTitik tertinggiKetinggian1.562 mdpl (5124 Kaki)Koordinat9°06′26″S 125°03′36″E / 9.107253°S 125.0599722°E / -9.107253; 125.0599722Koordinat: 9°06′26″S 125°03′36″E / 9.107253°S 125.0599722°E / -9.107253; 125.0599722 GeografiGunung LakaanLetak Gunung Lakaan di Pulau TimorTampilkan peta Pulau TimorGunung LakaanGunung Lakaan (Nusa Tenggara Timur)Tampilkan peta Nusa Tenggara TimurLetakKabupaten Belu, Nusa Ten...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Ionization technique used in mass spectroscopy A schematic diagram of chemical ionization source Chemical ionization (CI) is a soft ionization technique used in mass spectrometry.[1][2] This was first introduced by Burnaby Munson and Frank H. Field in 1966.[3] This technique is a branch of gaseous ion-molecule chemistry.[2] Reagent gas molecules (often methane or ammonia)[4] are ionized by electron ionization to form reagent ions, which subsequently rea...

لدائنمنتجات وأغراض مصنوعة من اللدائنمعلومات عامةصنف فرعي من مادة المواد المستخدمة وقود أحفوريمبلمر تعديل - تعديل مصدري - تعديل ويكي بيانات أنموذج لجزيء البوليبروبيلين - الكرات الزرقاء تمثل ذرات الكربون، والرمادية الهيدروجين اللدائن * هي مجموعة واسعة من المواد الاصطناعية...

† Египтопитек Реконструкция внешнего вида египтопитека Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:Четвероно...

Official Opposition Shadow Cabinet of the 42nd Parliament of CanadaShadow Cabinet of CanadaDate formedNovember 4, 2015People and organizationsHead of stateQueen Elizabeth IIOpposition partyConservative Party of CanadaOpposition leaderRona Ambrose (2015–2017)Andrew Scheer (2017–2019)HistoryElection(s)2015Legislature term(s)42nd Canadian ParliamentPredecessor41st (2011–2015)Successor43rd (2019–2021) Politics of Canada Government (structure) The Crown Monarch (list): Charles III Governo...

Davidoff Swiss Indoors 1981 Sport Tennis Data 12 ottobre – 18 ottobre Edizione 12a Superficie Cemento indoor Campioni Singolare Ivan Lendl Doppio José Luis Clerc / Ilie Năstase 1980 1982 Il Davidoff Swiss Indoors 1981 è stato un torneo di tennis giocato sul cemento indoor. È stata la 12ª edizione del torneo, che fa parte del Volvo Grand Prix 1981. Si è giocato a Basilea in Svizzera dal 12 al 18 ottobre 1981. Indice 1 Campioni 1.1 Singolare maschile 1.2 Doppio maschile 2 Collegamenti ...

Life-threatening allergic reaction Medical conditionAnaphylaxisSpecialtyAllergy and immunologySymptomsItchy rash, throat swelling, numbness, shortness of breath, lightheadedness, low blood pressure[1]Usual onsetOver minutes to hours[1]TypesAnaphylactoid reaction, anaphylactic shock, biphasic anaphylaxisCausesInsect bites, foods, medications[1]Diagnostic methodBased on symptoms[2]Differential diagnosisAllergic reaction,, asthma exacerbation, carcinoid syndrome&#...

Municipality in Veracruz, MexicoUxpanapaMunicipalityUxpanapaLocation in MexicoCoordinates: 17°17′0″N 94°27′0″W / 17.28333°N 94.45000°W / 17.28333; -94.45000Country MexicoStateVeracruzMunicipal seatLa Chinantla (Poblado 10)Municipality created31 January 1997Government • Municipal PresidentJuan Cuauhtémoc Vargas Mendoza (AFV)Area • Total2,600 km2 (1,000 sq mi)Elevation38 m (125 ft)Population (2005)&#...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Private university in Tusculum, Tennessee, U.S. A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (September 2017) (Learn how and when to remove this message) Tusculum UniversityFormer namesGreeneville College (1794–1868)Tusculum Academy (1818–1844)Tusculum College (1844–1868)Greeneville & Tusculum Col...

Untuk kegunaan lain, lihat Demi Cinta. Demi CintaSutradaraMatnoor TindaonProduserMerry GultomSoegiman DjajaprawiraDitulis olehNarto ErawanPemeranSophan SophiaanWidyawatiAedy MowardDina MarianaFadlyMansjur SjahMieke WijayaUci IndrajayaDistributorPanorama FilmTanggal rilis1974Durasi96 menitNegaraIndonesia Demi Cinta adalah film Indonesia yang dirilis pada tahun 1974 dengan disutradarai oleh Matnoor Tindaon. Film ini dibintangi antara lain oleh Sophan Sophiaan dan Widyawati. Sinopsis Johan (Soph...

1965 single by the Rolling Stones (I Can't Get No) SatisfactionUS picture sleeveSingle by the Rolling StonesB-side The Under Assistant West Coast Promotion Man (US) The Spider and the Fly (UK) Released 4 June 1965 (US) 20 August 1965 (UK) Recorded12 May 1965StudioRCA, HollywoodGenre Rock[1][2] Length3:45Label London (US) Decca (UK) Songwriter(s)Jagger–RichardsProducer(s)Andrew Loog OldhamThe Rolling Stones singles chronology The Last Time (1965) (I Can't Get No) Satisfaction...

Jodhi YudonoLahirJodhi Yudono(1963-05-16)16 Mei 1963Cilacap, Jawa TengahPekerjaanMusikus, Penulis, WartawanTahun aktif1986 - sekarang Jodhi Yudono (lahir 16 Mei 1963) adalah musikus dan penulis berkebangsaan Indonesia. Karya musiknya, dalam bentuk nyanyian puisi, dibawakan di panggung-panggung konvensional, dan juga dipersembahkan untuk menghibur kepada sesama kawan yang tengah mengalami penderitaan. Jodhi juga sering terlibat langsung dalam penggalangan dana kemanusiaan bagi daerah-dae...

1979 single by Joe Jackson Not to be confused with Different for Girls. It’s Different for GirlsSingle by Joe Jacksonfrom the album I'm the Man B-sideFriday (UK)Come On (US)Released30 Nov 1979 (UK)RecordedMarch 1979TW Studios, Fulham, LondonGenreNew waveLength3:42LabelA&MSongwriter(s)Joe JacksonProducer(s)David KershenbaumJoe Jackson singles chronology I'm the Man (1979) It’s Different for Girls (1979) Kinda Kute (1980) It’s Different for Girls is a song by Joe Jackson appearing on ...

Dewan Perwakilan Rakyat Daerah Kabupaten MunaDewan Perwakilan RakyatKabupaten Muna2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai16 Oktober 2019PimpinanKetuaLa Saemuna (Hanura) sejak 7 November 2019 Wakil Ketua IMuhammad Natsir Ido (Golkar) sejak 7 November 2019 Wakil Ketua IICahwan (Demokrat) sejak 7 November 2019 KomposisiAnggota30Partai & kursi PDI-P (4) NasDem (2) PKB (4) Hanura (5) Demokr...

Temperate grassland biome in Hungary This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Puszta – news · newspapers · books · scholar · JSTOR (January 2022) (Learn how and when to remove this message) PusztaEcologyRealmEurasian SteppeBiometemperate grasslandGeographyCountryHungaryCoordinates47°30′N 21°06′E...