Мадлен Савойская
| |||||||||||||||||||||||||||||||||||||||||
Read other articles:

Cenarchaeum Klasifikasi ilmiah Domain: Archaea Kerajaan: Crenarchaeota Filum: Thaumarchaeota Kelas: incertae sedis Ordo: Cenarchaeales Famili: Cenarchaeaceae Genus: Cenarchaeum Spesies C. symbiosum uncultured Cenarchaeum sp. Sinonim Cenarchaeum DeLong and Preston 1996 Dalam taksonomi, Cenarchaeum adalah genus dari Cenarchaeaceae.[1] Arkea laut Cenarchaeum symbiosum hidup di dalam (itu adalah endosimbion dari) spons Axinella mexicana.[2] Referensi ^ See the NCBI webpage on Cen...

Keuskupan CaltanissettaDioecesis CalatanisiadensisKatolik Katedral di CaltanissettaLokasiNegara ItaliaProvinsi gerejawiAgrigentoStatistikLuas1.120 km2 (430 sq mi)Populasi- Total- Katolik(per 2013)166.874164,000 (est.) (98.3%)Paroki56Imam102 (diosesan)13 (Ordo Relijius)InformasiDenominasiGereja KatolikRitusRitus RomaPendirian25 Mei 1844 (179 tahun lalu)KatedralCattedrale di S. Maria La NovaKepemimpinan kiniPausFransiskusUskupMario RussottoPetaSitus webww...
Aicha vorm Wald Gereja Paroki Aicha vorm Wald Lambang kebesaranLetak Aicha vorm Wald NegaraJermanNegara bagianBayernWilayahNiederbayernKreisPassauSubdivisions32 OrtsteilePemerintahan • MayorGeorg Hatzesberger (CSU)Luas • Total20,32 km2 (785 sq mi)Ketinggian tertinggi532 m (1,745 ft)Ketinggian terendah335 m (1,099 ft)Populasi (2013-12-31)[1] • Total2.437 • Kepadatan1,2/km2 (3,1/sq mi)...

Athletics at the1989 Summer UniversiadeTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen3000 mwomen5000 mmen10,000 mmenwomen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmenwomen3000 msteeplechasemen4×100 m relaymenwomen4×400 m relaymenwomenRoad eventsMarathonmenwomen5 km walkwomen20 km walkmenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin throwmenwomenCombined eventsHeptathlo...

For the similarly named adjoining municipality, see Cuautitlán Izcalli. For the Tren Suburbano station, see Cuautitlán railway station. Town & Municipality in State of Mexico, MexicoCuautitlánTown & MunicipalityCuautitlánCoordinates: 19°40′20″N 99°10′50″W / 19.67222°N 99.18056°W / 19.67222; -99.18056Country MexicoStateState of MexicoMunicipal Status1861Government • Municipal PresidentAldo Ledezma Reyna (2022-2024)Area ...

ATF Dingo Angkatan Darat Jerman adalah kendaraan mobilitas infanteri yang terlindungi dengan baik yang digunakan oleh beberapa angkatan bersenjata Eropa Kendaraan mobilitas infanteri (KMI) atau Infantry Mobility Vehicle (IMV) adalah kendaraan pengangkut personel lapis baja (APC) beroda yang berfungsi sebagai kendaraan patroli militer, pengintaian, atau keamanan. Contohnya termasuk ATF Dingo, Iveco LMV, Oshkosh M-ATV, AMZ Dzik, AMZ Tur, Mungo ESK, and Bushmaster IMV. This term also applies to ...

See also: 1916 Major League Baseball season The following are the baseball events of the year 1916 throughout the world. Overview of the events of 1916 in baseball Years in baseball ← 1913 1914 1915 1916 1917 1918 1919 → 1916 in sports Air sports American football Aquatic sports Association football Athletics Badminton Baseball Basketball Canadian football Chess Climbing Combat sports Sumo Cricket 1915–16 1916 1916–17 Cycling Dance sports Darts Equestrianism Esports Field hockey Flyin...

Protected area in New South Wales, AustraliaBroulee Island Nature ReserveNew South WalesIUCN category IV (habitat/species management area) Broulee Island looking south from Burri PointBroulee Island Nature ReserveNearest town or cityBrouleeCoordinates35°51′28″S 150°11′18″E / 35.85778°S 150.18833°E / -35.85778; 150.18833EstablishedApril 1972 (1972-04)[1]Area0.43 km2 (0.2 sq mi)[1]Managing authoritiesNSW National Park...

Zvonimir Boban Nazionalità Jugoslavia Croazia (dal 1991) Altezza 183 cm Peso 73 kg Calcio Ruolo Centrocampista Termine carriera 2001 - giocatore Carriera Giovanili 1978-1981 Mračaj Runović1981-1982 Hajduk Spalato1983-1985 Dinamo Zagabria Squadre di club1 1985-1991 Dinamo Zagabria109 (45)1991-1992→ Bari17 (2)1992-2001 Milan178 (21)2001→ Celta Vigo4 (0) Nazionale 1987 Jugoslavia U-206 (3)1988-1991 Jugoslavia7 (1)1992-1999 Croazia51 (12) Pa...

Capital and largest city of Russia Not to be confused with Moscow Oblast. Moskva redirects here. For other uses, see Moscow (disambiguation) and Moskva (disambiguation). This article may be too long to read and navigate comfortably. When this tag was added, its readable prose size was 15,546 words. Consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (March 2024) Capital city and federal city in RussiaMoscow ...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Said HidayatPotret resmi Said Hidayat sebagai Bupati Boyolali Bupati Boyolali ke-25PetahanaMulai menjabat 26 Februari 2021PresidenJoko WidodoGubernurGanjar PranowoNana Sudjana (Pj.)WakilWahyu IrawanPendahuluSeno SamodroPenggantiPetahanaWakil Bupati BoyolaliMasa jabatan17 Februari 2016 – 17 Februari 2021PresidenJoko WidodoGubernurGanjar PranowoBupatiSeno SamodroPendahuluAgus PurmantoPenggantiWahyu Irawan Informasi pribadiLahirMohammad Said Hidayat7 September 1972 (umur ...
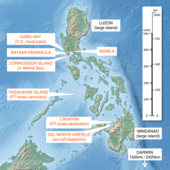
World War II escape PT-32, one of the four PT-20 class motor torpedo boats involved in the first part of the journey On 11 March 1942, during World War II, General Douglas MacArthur and members of his family and staff left the Philippine island of Corregidor and his forces, which were surrounded by the Japanese. They traveled in PT boats through stormy seas patrolled by Japanese warships and reached Mindanao two days later. From there, MacArthur and his party flew to Australia in a pair of Bo...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

この項目では、フジテレビのバラエティ番組について説明しています。KBCラジオのワイド番組については「スター高橋 ドッキリ!マル秘報告」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年3月) 独自研究が含まれて...

1883–1906 gold rush in Argentina Tierra del Fuego Gold RushAn 1889 5-gram gold coin from Tierra del Fuego by Julius PopperDate1883–1906LocationTierra del Fuego, Argentina and ChileCauseGold rush began after the French steamship Arctique ran aground on the northern coast of Cape Virgenes and a rescue expedition for the stranded crew discovered gold in Zanja a PiqueParticipantsChilean minersArgentine minersDalmatian minersOther European minersOutcomeInflux of miners led to the formation of ...

” ما أعمق غنى الله، وحكمته، وعلمه! ما أبعد أحكامه عن الفحص، وطرقه عن التتبع! لأنه من عرف فكر الرب؟ أو من كان له مشيرًا؟ أو من أقرضه شيئًا حتى يُردّ له؟ فإنّ منه، وبه، وله، كل شيء. له المجد إلى الأبد. آمين. “ —بولس، الرسالة إلى روما، 11: 33 - 36. الله في المسيحية، هو إله واحد...

Joseph Louis François Bertrand Existence of a prime number between any number and its double In number theory, Bertrand's postulate is the theorem that for any integer n > 3 {\displaystyle n>3} , there exists at least one prime number p {\displaystyle p} with n < p < 2 n − 2. {\displaystyle n<p<2n-2.} A less restrictive formulation is: for every n > 1 {\displaystyle n>1} , there is always at least one prime p {\displaystyle p} such that n < p < 2 n . {\di...

gennaio · febbraio · marzo · aprile · maggio · giugno · luglio · agosto · settembre · ottobre · novembre · dicembre 2024 Do Lu Ma Me Gi Ve Sa Do Lu Ma Me Gi Ve Sa Do Lu Ma Me Gi Ve Sa Do Lu Ma Me Gi Ve Sa Do Lu Ma ← 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 → Il 14 dicembre è il 348º giorno del calendario gregoriano (il 349º negli anni bisestili). Mancano 17 giorni alla ...

