–Ы–µ–Љ–Љ–∞ –Њ —А—Г–Ї–Њ–њ–Њ–ґ–∞—В–Є—П—Е
|
Read other articles:

Lokasi Provinsi Fujian (merah) Sejarah Fujian adalah suatu periode panjang kemunculan manusia dan perkembangannya di Provinsi Fujian, Tiongkok. Sejarah provinsi ini berbeda dengan sebagian besar Tiongkok, dengan penduduk asli yang kemudian ditaklukkan dan diserap ke dalam populasi bangsa Tionghoa yang datang dari Dataran Tengah Tiongkok. Awal sejarah Pengaruh Tionghoa terhadap Fujian tercatat datang agak terlambat.[1] Sampai akhir periode Dinasti Han, daerah ini dianggap kosong, semen...

Burung hantu kelabu besar Status konservasi Risiko Rendah Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Strigiformes Famili: Strigidae Genus: Strix Spesies: S. nebulosa Nama binomial Strix nebulosaForster, 1772 Strix nebulosa lapponica Burung hantu kelabu besar (Great Gray Owl atau Strix nebulosa) adalah salah satu spesies burung hantu yang pertama kali dideskripsikan oleh Johann Reinhold Forster (seorang naturalis yang mengikuti perjalanan Kapten James Cook pa...

1988 film by Rajasekhar Paatti Sollai ThattathePosterDirected byRajasekharWritten byChithralaya GopuProduced byM. SaravananM. BalasubramanianM. S. GuhanStarringPandiarajanUrvashiManoramaCinematographyV RangaEdited byR. VittalC. LaasniMusic byChandraboseProductioncompanyAVM ProductionsRelease date 22 July 1988 (1988-07-22) Running time148 minutesCountryIndiaLanguageTamil Paatti Sollai Thattathe (transl. Do not disobey your grandmother's words) is a 1988 Indian Tamil-langua...

Lost ancient Greek epic The Sack of Troy redirects here. For the late Roman epic by Tryphiodorus, see Tryphiodorus ¬І The Taking of Ilios. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Iliupersis вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (September 2015) (Learn how and when to remove this template...
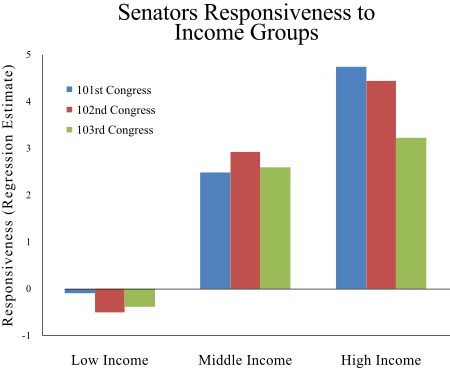
Social class in the United States The American upper class is a social group within the United States consisting of people who have the highest social rank, due to a lineage associated with wealth, pedigree, and economic wealth.[1][2] The American upper class is distinguished from the rest of the population due to the fact that its primary source of income consists of assets, investments, and capital gains rather than wages and salaries. The American upper class is estimated t...

Ulangan 31Halaman yang memuat Ulangan 32:50-33:29 pada Kodeks Aleppo (~920 M)KitabKitab UlanganKategoriTauratBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen5← pasal 30 pasal 32 → Ulangan 31 (disingkat Ul 31) adalah bagian dari Kitab Ulangan dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen yang merupakan kitab ke-5 dan terakhir dalam kumpulan kitab Taurat yang disusun oleh Musa.[1][2] Teks Naskah sumber utama: Masoretik, Taurat Samaria, Sep...

American football player and coach (1890вАУ1945) A. G. ScanlanBiographical detailsBorn(1890-08-16)August 16, 1890Chicago, Illinois, U.S.DiedJuly 8, 1945(1945-07-08) (aged 54)Chicago, Illinois, U.S.Playing career1912вАУ1913Chicago Coaching career (HC unless noted)1918вАУ1920Purdue Head coaching recordOverall7вАУ12вАУ1Accomplishments and honorsChampionships1 Big Ten (1918) Arthur Garrett Butch Scanlan (August 16, 1890 вАУ July 8, 1945) was an American football coach. He served as the head ...

Australian murderer and serial child rapist Brett Peter CowanBorn (1969-09-18) 18 September 1969 (age 54)Bunbury, Western AustraliaCriminal statusIncarceratedConviction(s)2014: Murder Deprivation of liberty Child stealing Indecent treatment of children under 16 Interfering with a corpse 1994: Gross indecency Grievous bodily harm Deprivation of liberty 1989:Indecent treatment of children under 16Criminal penaltyLife imprisonment with the possibility of parole after 20 years (August 2031)D...

Ў≥Ў®ЎІўВ ЎЈўИЎІўБ ўБЎ±ўЖЎ≥ЎІ 1981 ЎІўДЎІЎ≥ўЕ Ў≥Ў®ЎІўВ ЎЈўИЎІўБ ўБЎ±ўЖЎ≥ЎІ 1981 ЎІўДЎ≥ўДЎ≥ўДЎ© Ў≥ўИЎ®Ў± Ў®Ў±Ў≥Ў™ўКЎђ Ў®ўКЎ±ўЖўИЎѓ 1981 ЎІўДЎ™ЎІЎ±ўКЎЃ 25 ўКўИўЖўКўИ - 19 ўКўИўДўКўИ 1981 ЎІўДЎ™ЎІЎ±ўКЎЃ Ў®ЎѓЎІўКЎ©:25 ўКўИўЖўКўИ 1981 ўЖўЗЎІўКЎ©:19 ўКўИўДўКўИ 1981 ЎєЎѓЎѓ ЎІўДўЕЎ±ЎІЎ≠ўД 22+Prologue, including two split stages ЎєЎѓЎѓ ЎІўДЎ±ўКЎІЎґўКўКўЖ 121 (ўЖўВЎЈЎ© ЎІўДўЖўЗЎІўКЎ©)ЎМ ўИ150 (ўЖўВЎЈЎ© ЎІўДЎ®ЎѓЎІўКЎ©) ЎІўДўЕЎ≥ЎІўБЎ© 3756.1 ЎІўДЎ≤ўЕўЖ 96 Ў≥ЎІЎєЎ© ўИ19 ЎѓўВпњљ...

American filmmaker (born 1946) Joe DanteDante in 2023BornJoseph James Dante Jr.[1] (1946-11-28) November 28, 1946 (age 77)[2]Morristown, New Jersey, U.S.Alma materUniversity of the ArtsThomas Jefferson UniversityOccupation(s)Director, producer, editor, actorYears active1968вАУpresentSpouseElizabeth StanleyWebsiterenfieldproductions.com Joseph James Dante Jr. (/ЋИd…СЋРnte…™/; born November 28, 1946) is an American filmmaker, producer, editor and actor. His filmsпњљ...

Un bitume routier (paving bitumen en anglais, Stra√Яenbaubitumen en allemand) est un bitume utilis√© pour lвАЩenrobage des granulats destin√©s √† la construction et l'entretien des routes et des structures assimil√©es. √Йpandage de mat√©riaux bitumineux en Turquie Sp√©cifications en Europe Compression du mat√©riau de r√©paration d'une tranch√©e dans une voirie urbaine. La norme europ√©enne EN-12591 d√©finit un cadre de sp√©cifications applicables sur lвАЩensemble des pays dвАЩEurope. Chaque p...
2020еєіе§Пе≠£е••жЮЧеМєеЕЛињРеК®дЉЪж≥ҐеЕ∞дї£и°®еЬШж≥ҐеЕ∞еЫљжЧЧIOC磮祊POLNOCж≥ҐиШ≠е•ІжЮЧеМєеЕЛеІФеУ°жЬГзґ≤зЂЩolimpijski.plпЉИиЛ±жЦЗпЉЙпЉИж≥ҐеЕ∞жЦЗпЉЙ2020еєіе§Пе≠£е••жЮЧеМєеЕЛињРеК®дЉЪпЉИжЭ±дЇђпЉЙ2021еєі7жЬИ23жЧ•иЗ≥8жЬИ8жЧ•пЉИеПЧ2019еЖ†зКґзЧЕжѓТзЧЕзЦЂжГЕељ±еУНжО®ињЯпЉМдљЖдїНдњЭзХЩеОЯеЃЪеРНзІ∞пЉЙйБЛеЛХеУ°206еПГи≥љй†ЕзЫЃ24дЄ™е§Ій°єжЧЧжЙЛеЉАеєХеЉПпЉЪеЄХзїіе∞Ф¬ЈзІСзГ≠е∞Ље••е§ЂжЦѓеЯЇпЉИжЄЄж≥≥пЉЙеТМй©ђе®Е¬Јж≤ГдїАдєФе§ЂжЦѓеН°пЉИиЗ™и°Миљ¶пЉЙ[1]йЧ≠еєХеЉПпЉЪеН°зљЧеИ©е®Ь¬ЈзЇ≥дЇЪпЉИзЪЃеИТиЙЗпЉЙ&#...

Coin-operated entertainment machine This article is about all types of amusement arcade games. For video games, see Arcade video game. Not to be confused with Casino game. An amusement arcade featuring several different types of arcade games, located in Chiba Prefecture, Japan An arcade game or coin-op game is a coin-operated entertainment machine typically installed in public businesses such as restaurants, bars and amusement arcades. Most arcade games are presented as primarily games of ski...

ўЕЎЈЎІЎ± ўИўДЎІўЖЎЇЎІЎ® Ulanqab Airport дєМеЕ∞еѓЯеЄГжЬЇеЬЇ Ў•ўКЎІЎ™ЎІ: UCB вАУ ЎІўКўГЎІўИ: ZBUC ўЕўИЎђЎ≤ ўЖўИЎє ЎІўДўЕЎЈЎІЎ± ЎєЎІўЕ ўКЎЃЎѓўЕ ЎІўИўДЎІўЖЎ™ЎіЎІЎ®ЎМ ўЕўЖЎЇўИўДўКЎІ ЎІўДЎѓЎІЎЃўДўКЎ© ЎІўДЎ®ўДЎѓ ЎІўДЎµўКўЖ ЎІўДўЕўИўВЎє ЎІўИўДЎІўЖЎ™ЎіЎІЎ® ўБўК ўЕўЖЎЇўИўДўКЎІ ЎІўДЎѓЎІЎЃўДўКЎ© Ў•Ў≠ЎѓЎІЎЂўКЎІЎ™ 41¬∞07вА≤47вА≥N 113¬∞06вА≤29вА≥E / 41.1298¬∞N 113.10802¬∞E / 41.1298; 113.10802 ЎІўДЎЃЎ±ўКЎЈЎ© Ў•Ў≠ЎµЎІЎ¶ўКЎІЎ™ Ў™ЎєЎѓўКўД ўЕЎµЎѓЎ±ўК - Ў™ЎєЎѓўКпњљ...

South Korean actor For South Korean actor of the same name born in 1984, see Lee Joon-hyuk (actor, born 1984). In this Korean name, the family name is Lee. Lee Jun-hyeokBorn (1972-03-19) March 19, 1972 (age 52)Jung District, Seoul, South KoreaOther namesLee Joon-hyukOccupationActorYears active1991вАУpresentAgentChang CompanySpouseJi Young-anChildren3Korean nameHangulмЭім§АнШБHanjaжЭОжЇЦиµЂRevised RomanizationI Jun-hyeokMcCuneвАУReischauerYi Chun-hy≈Пk Lee Jun-hyeok[1] (...

Drawing the retorts at the Great Gas Establishment Brick Lane, from The Monthly Magazine (1821) The history of gaseous fuel, important for lighting, heating, and cooking purposes throughout most of the 19th century and the first half of the 20th century, began with the development of analytical and pneumatic chemistry in the 18th century. These synthetic fuel gases (also known as manufactured fuel gas, manufactured gas or simply gas) were made by gasification of combustible materials, usuall...

Open standard for office applications Uniform Office FormatFilename extension .uof, .uot, .uos, .uopInitial releaseApril 30, 2007; 17 years ago (2007-04-30)Latest release2.02011; 13 years ago (2011) Type of formatDocument file formatExtended fromXML, SVGStandardGB/T20916-2007Open format?Yes Uniform Office Format (UOF; Chinese ж†ЗжЦЗйАЪ, literally standard text general[1]), sometimes known as Unified Office Format, is an open standard for office...

British Lions & Scotland international rugby union player For other uses, see Scott Hastings (disambiguation). Rugby playerScott HastingsDate of birth (1964-12-04) 4 December 1964 (age 59)Place of birthEdinburgh, ScotlandHeight1.85 m (6 ft 1 in)Weight91 kg (14 st 5 lb; 201 lb)SchoolGeorge Watson's CollegeNotable relative(s)Kerry-Anne Hastings, daughterAdam Hastings, nephewGavin Hastings, brotherRugby union careerPosition(s) Outside centreAmateur tea...

Cet article traite de l'√©quipe masculine. Pour l'√©quipe f√©minine, voir √Йquipe de France de football australien f√©minin. Pour les articles homonymes, voir √Йquipe de France. France Informations-cl√©s Surnom Coqs Couleurs Bleu, blanc, rouge F√©d√©ration Comit√© national de football australien Classement WFN 10e (octobre 2022)[1] S√©lectionneur Andrew Unsworth Capitaine Gr√©goire Patacq Record de s√©lections Joevin L'Hotelier Olivier Tresca (14) Premier match officiel Su√®de 81-42 France (...

Questa voce o sezione sull'argomento film di fantascienza non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Molti paragrafi mancano delle opportune fonti Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Fluido mortaleI titoli di testaTitolo originaleThe Blob Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1958 Durata86 min G...












