Закон Гудхарта
|
Read other articles:

Infanta BeatrizAdipati wanita ViseuGambaran Infanta Beatriz pada tahun 1678 di dalam Biara BejaKelahiran13 Juni 1430Kematian30 September 1506 (usia 76 tahun)WangsaWangsa AvizAyahJoãoIbuIsabel dari BarcelosPasanganFernando dari ViseuAnakManuel I dari PortugalLeonor dari ViseuIsabel dari ViseuTanda tangan Infanta Beatriz dari Portugal (13 Juni 1430 – 30 September 1506) merupakan seorang Infanta Portugis, putri João (putra keempat Raja João I dari Portugal dan istrinya Filipa dari Lancaster...

Bagian dari seriFeminisme Wanita Gadis Femininitas Sejarah Sosial Sejarah wanita Sejarah feminis Sejarah feminisme Sejarah wanita Indonesia Sejarah wanita Amerika Sejarah wanita Kanada Sejarah wanita Jerman Sejarah wanita di Britania Raya Linimasa Hak pilih wanita Negara mayoritas Muslim Amerika Serikat Hak wanita lainnya Hak pilih menurut negara Australia Kanada Jepang Kuwait Selandia Baru Swedia Swiss Britania Raya Wales Amerika Serikat Di negara bagian Utah Gelombang Pertama Kedua Ketiga K...

Universitas SjakhyakirtiRektorDr.Ir. Agoes Thony AK, M.Si Universitas Sjakhyakirti adalah perguruan tinggi swasta di Palembang, Indonesia. Perguruan tinggi ini berdiri pada tahun 1 April 1953. Rektor pada tahun 2022 adalah Dr.Ir. Agoes Thony AK, M.Si . Sejarah Perguruan tinggi ini merupakan perguruan tinggi tertua dan merupakan pelopor pendidikan tinggi di Sumatera Selatan. Perguruan tinggi yang didirikan pada tanggal 1 April 1953 oleh H. R.H.A. Rani yang saat itu membina fakultas hukum dan i...

العلاقات الإماراتية اللاوسية الإمارات العربية المتحدة لاوس الإمارات العربية المتحدة لاوس تعديل مصدري - تعديل العلاقات الإماراتية اللاوسية هي العلاقات الثنائية التي تجمع بين الإمارات العربية المتحدة ولاوس.[1][2][3][4][5] مقارنة بين البلد...

Subspecies of honey bee This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Carniolan honey bee – news · newspapers · books · scholar · JSTOR (July 2016) (Learn how and when to remove this template message) Carniolan honey bee Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class...

American basketball player (born 1995) Jabari ParkerParker with the Milwaukee Bucks in 2014No. 22 – FC BarcelonaPositionPower forwardLeagueLiga ACBEuroLeaguePersonal informationBorn (1995-03-15) March 15, 1995 (age 29)Chicago, Illinois, U.S.Listed height6 ft 8 in (2.03 m)Listed weight250 lb (113 kg)Career informationHigh schoolSimeon (Chicago, Illinois)CollegeDuke (2013–2014)NBA draft2014: 1st round, 2nd overall pickSelected by the Milwaukee BucksPlay...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Pour les articles homonymes, voir Full Circle. Cet article est une ébauche concernant l’informatique et Internet. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Logo du Full Circle Magazine Le Full Circle Magazine est un magazine en ligne anglophone amateur gratuit ayant pour sujet la distribution GNU/Linux Ubuntu et ses dérivés Kubuntu, Xubuntu et Edubuntu. Présentation Le magazine se définit lui-même ...

Trigonometri Garis besar Sejarah Kegunaan Fungsi (invers) Trigonometri rampat Rujukan Identitas Nilai eksak Tabel Satuan lingkaran Aturan dan teorema Sinus Kosinus Tangen Kotangen Teorema Pythagoras Kalkulus Substitusi trigonometri Integral (fungsi invers) Turunan lbs Dasar trigonometri mengatakan bahwa jika dua segitiga siku-siku mempunyai sudut lancip yang sama, maka segitiga dikatakan sebangun sehingga panjang sisinya sebanding. Dalam matematika, fungsi trigonometri merupakan fun...

This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Kamaljit Bawa – news · newspapers · books · scholar · JSTOR (July 2018) (Learn how and when to remove this message) Kamal BawaKamaljit Singh Bawa ...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Bulgarian footballer In this Bulgarian name, the patronymic is Lyudmilov and the family name is Chochev. Ivaylo Chochev Chochev playing for CSKA in 2013Personal informationFull name Ivaylo Lyudmilov ChochevDate of birth (1993-02-18) 18 February 1993 (age 31)Place of birth Pleven, BulgariaHeight 1.88 m (6 ft 2 in)[1]Position(s) MidfielderTeam informationCurrent team Ludogorets RazgradNumber 18Youth career1999–2008 Spartak Pleven2008–2010 Chavdar EtropoleSeni...

German jurist and essayist Jung, c. 1925 This article is part of a series onConservatism in Germany Ideologies Agrarian Christian democracy Liberal Ordo Ritter School Monarchism Nationalist Neue Rechte Völkisch Paternalistic State Socialism Prussianism Cameralistic Socialist Revolutionary Young Romanticism Right-Hegelianism Historical School Principles Christian values Duty Elitism Aristocracy Meritocracy Gemeinschaft Heimat In Treue fest Kultur Medievalism Monarchism Organicism Patrio...
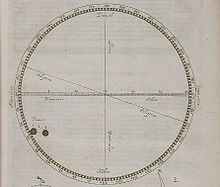
English astronomer (1618–1641) Jeremiah HorrocksRomanticised Victorian painting of Horrocks making the first observation of the transit of Venus in 1639. No contemporary portraits of Horrocks survive.[1]Born1618Lower Lodge, Otterspool,Toxteth Park, Liverpool, Lancashire, EnglandDied3 January 1641 (aged 22)Toxteth Park, Liverpool, Lancashire, EnglandAlma materUniversity of CambridgeKnown forTransit of Venus Tides Elliptical orbit Lunar orbitScientific careerFieldsAstronomy ...

Pashtun tribe For a list of people with Durrani as a surname, see Durrani (surname). Ethnic group DurraniدرانيCoronation of Ahmad Shah Durr-i-Durrān by Abdali chiefs at Kandahar in 1747Regions with significant populationsAfghanistan PakistanLanguagesPashtoReligion Islam The Durrānī (Pashto: دراني, pronounced [durɑˈni]1), formerly known as Abdālī (ابدالي), are one of the largest tribes of Pashtuns. Their traditional homeland is in southern Afghanistan (Loy ...

Cyrillic letter Cyrillic letterU with graveThe Cyrillic scriptSlavic lettersАА̀А̂А̄ӒБВГҐДЂЃЕЀЕ̄Е̂ЁЄЖЗЗ́ЅИІЇꙆЍИ̂ӢЙЈКЛЉМНЊОО̀О̂ŌӦПРСС́ТЋЌУУ̀У̂ӮЎӰФХЦЧЏШЩꙎЪЪ̀ЫЬѢЭЮЮ̀ЯЯ̀Non-Slavic lettersӐА̊А̃Ӓ̄ӔӘӘ́Ә̃ӚВ̌ԜГ̑Г̇Г̣Г̌Г̂Г̆Г̈г̊ҔҒӺҒ̌ғ̊ӶД́Д̌Д̈Д̣Д̆ӖЕ̃Ё̄Є̈ԐԐ̈ҖӜӁЖ̣ҘӞЗ̌З̣З̆ӠИ̃ӤҊҚӃҠҞҜК̣к̊қ̊ԚᴫЛ́ӅԮԒЛ̈ӍᵸН́ӉҢԨӇҤО̆О�...

1934 film The Voice of LoveMaria Beling and Marcel WittrischDirected byVictor JansonWritten byPaul Beyer (idea)Peter FranckeWalter WassermannProduced byErich SchickerKarl SchulzRobert WüllnerStarringMarcel WittrischMaria BelingMarieluise ClaudiusCinematographyCarl DrewsEdited byRoger von NormanMusic byEduard KünnekeProductioncompanyTerra FilmDistributed byTerra FilmRelease date 3 January 1934 (1934-01-03) Running time76 minutesCountryGermanyLanguageGerman The Voice of Love (G...

.ac Введение 1997 Тип домена национальный домен верхнего уровня Статус действующий Регистратура Ascension Island Network Information Centre Организатор Cable and Wireless (остров Вознесения) Назначение Объекты, связанные с островом Вознесения Использование Ряд сайтов, посвящённых острову Вознесени�...

TNPO2 معرفات أسماء بديلة TNPO2, IPO3, KPNB2B, TRN2, transportin 2 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 603002 MGI: MGI:2384849 HomoloGene: 8381 GeneCards: 30000 علم الوجود الجيني وظائف جزيئية • GO:0001948، GO:0016582 ربط بروتيني• nuclear localization sequence binding مكونات خلوية • غلاف نووي• nuclear periphery• نواة• سيتوبلازم عم...