Двойное покрытие двудольным графом
|
Read other articles:

Artikel ini bukan mengenai Bahasa Rusyn. Bahasa Rusia Raya beralih ke halaman ini, yang bukan mengenai Rusia Raya. Cari artikel bahasa Cari berdasarkan kode ISO 639 (Uji coba) Kolom pencarian ini hanya didukung oleh beberapa antarmuka Halaman bahasa acak Bahasa Rusia русский язык[cat. 1] Pengucapan[ˈruskʲɪj jɪˈzɨk] ⓘDituturkan diRusia dan wilayah-wilayah lain bekas Uni SovietWilayahDunia berbahasa RusiaEtnisRusiaPenuturB2 150 juta (201...

Estonian football club Football clubJK Eesti Põlevkivi Jõhviinformation at time of demiseFull nameJalgpalliklubi Eesti Põlevkivi JõhviFounded1974Dissolved1999GroundJõhvi linnastaadion, JõhviCapacity2,000Chairman –Manager –League –1999Meistriliiga, 8th Home colours Away colours JK Eesti Põlevkivi Jõhvi was an Estonian football club based in Jõhvi and was founded in 1974.[1] EP Jõhvi became the first Estonian runner-up after the Soviet Union collapse and a...

DalLentil adalah bahan pokok dalam masakan dari subbenua India. Searah jarum jam dari kanan atas: belah lentil merah, lentil hijau utuh yang umum, dan lentil Le Puy. Seluruh lentil memiliki lapisan luar yang terlihat.Nama lainDaal, dail, dhal, dahlTempat asalSubbenua IndiaDaerahSubbenua IndiaBahan utamaLentil, kacang polong atau kacang-kacanganSunting kotak info • L • BBantuan penggunaan templat ini Buku resep: Dal Media: Dal Dal adalah istilah yang digunakan di subben...

Depiction of the British capture of Martinique which took place in 1809 vteWest Indies campaign (1803–1810) Saint-Domingue St Lucia • Tobago • Demerara • Essequibo and Berbice Surinam Diamond Rock San Domingo Havana Samaná Jeune Richard Danish West Indies Palo Hincado Santo Domingo French Guiana Pointe Noire Martinique Leeward Islands Troude's expedition Roquebert's expedition Guadeloupe vteNapoleonic Wars Third Coalition Anglo-Spanish War Russo-Persian War Franco-Swedish War Fourth...

Campionato Nazionale Dante Berretti 1997-1998 Competizione Campionato nazionale Dante Berretti Sport Calcio Edizione 32ª Organizzatore Lega Italiana Calcio Professionistico Luogo Italia Partecipanti 95 Risultati Vincitore Lodigiani (Serie C1-C2) Cronologia della competizione 1996-97 1998-99 Manuale Il Dante Berretti 1997-1998 è stato la 32ª edizione del campionato nazionale Dante Berretti, la 2ª per le squadre giovanili delle sole società di Serie C. Il detentore del trofeo ...

Questa voce o sezione sull'argomento aerei non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. L'aerosilurante è un particolare aereo da bombardamento che al posto di convenzionali bombe aeree trasporta uno o più siluri. Indice 1 Descrizione 2 Lista di aerosiluranti 3 Voci correlate 4 Altri progetti 5 C...

Untuk kegunaan lain, lihat Legrand (marga). Mirtha LegrandMirtha Legrand pada 2013LahirRosa María Juana Martínez Suárez23 Februari 1927 (umur 97)Villa Cañás, ArgentinaNama lainChiquita, ChiquiPekerjaanPemeran, pemandu acaraTahun aktif1940–2020Televisi Almorzando con Mirtha Legrand (1968–2020) La Dueña (2012)[1] Suami/istriDaniel Tinayre (1946–1994)Anak Daniel Andrés Tinayre Marcela Tinayre Rosa María Juana Martínez Suárez (lahir 23 Februari 1927), bernam...

Internal limits, authorizations and directives on use of force in combat For other uses, see Rules of Engagement (disambiguation). The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (April 2014) (Learn how and when to remove this message) Rules of Engagement for Operation Provide Relief, 1992 Rules of engagement (ROE) are the internal rules or...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Este artículo trata de una propiedad de los colores como los colores primarios. Para otras acepciones, véase saturación Diferentes niveles de saturación de una misma imagen. En la teoría del color, el colorido, el croma o la saturación es la intensidad de un matiz específico. Se basa en la pureza del color; un color muy saturado tiene un color vivo e intenso, mientras que un color poco saturado parece más descolorido y gris. Sin saturación, un color se convierte en un tono de gris o ...

Cabinet of Bangladesh (2024-) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Fifth Hasina ministry – news · newspapers · books · scholar · JSTOR (January 2024) Fifth Hasina Ministry21st Cabinet of BangladeshSheikh Hasina Wazed Hon'ble Prime Minister of BangladeshDate formed11 January 202...
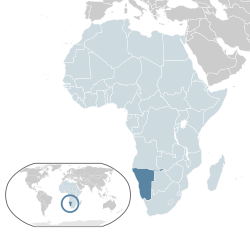
Country in Southern Africa For the newspaper, see The Namibian. Republic of Namibia Name in national languages Afrikaans:Republiek van Namibië[1]German:Republik Namibia [2]Khoekhoegowab:Republiki Namibiab dib[3]Oshiwambo:Orepublika yaNamibia[4]Otjiherero:Orepublika yaNamibia[5]RuKwangali:Republika zaNamibia[6]Setswana:Rephaboliki ya Namibia[7]siLozi:Namibia ye Lukuluhile[8] Flag Coat of arms Motto: Unity, Liberty, JusticeAn...

Saint-Côme-et-MaruéjolscomuneSaint-Côme-et-Maruéjols – Veduta LocalizzazioneStato Francia RegioneOccitania Dipartimento Gard ArrondissementNîmes CantoneSaint-Gilles TerritorioCoordinate43°49′N 4°12′E43°49′N, 4°12′E (Saint-Côme-et-Maruéjols) Altitudine42 m s.l.m. Superficie12,81 km² Abitanti796[1] (2009) Densità62,14 ab./km² Altre informazioniCod. postale30870 Fuso orarioUTC+1 Codice INSEE30245 CartografiaSaint-Côme-et-Maruéjols Sito ...

Motion-sensing input device for the Xbox 360 and Xbox One Skeletal tracking redirects here. For other skeletal tracking systems, see Gesture recognition and Motion capture. KinectKinect for Xbox OneDeveloperMicrosoftTypeMotion controllerGenerationSeventh and eighthRelease dateXbox 360 NA: November 4, 2010[2]EU: November 10, 2010[1]COL: November 14, 2010[3]AU: November 18, 2010[4]JP: November 20, 2010[5]Microsoft Windows WW: February 1, 2012[6]Xb...

Association football club in England Football clubEast Thurrock UnitedFull nameEast Thurrock United Football ClubNickname(s)The RocksFounded27 April 1969Dissolved1 September 2023GroundRookery Hill, CorringhamCapacity3,500[1]WebsiteClub website Home colours Away colours East Thurrock United Football Club was a football club based in Corringham, Essex, England. They last competed in Isthmian League North Division and played at Rookery Hill. The club was placed into liquidation by owner ...

System of connected p-orbitals with delocalized electrons in a molecule Cinnamaldehyde is a naturally-occurring compound that has a conjugated system penta-1,3-diene is a molecule with a conjugated system Diazomethane conjugated pi-system In theoretical chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in a molecule, which in general lowers the overall energy of the molecule and increases stability. It is conventionally represented as having alterna...

Haymakers redirects here. For other uses, see Haymaker. 1999 studio album by Paul McCartney with the London Symphony Orchestra and the Loma Mar QuartetWorking ClassicalStudio album by Paul McCartney with the London Symphony Orchestra and the Loma Mar QuartetReleased1 November 1999Recorded1998–1999StudioEMI Studios, Abbey RoadGenreClassical, chamber musicLength61:35LabelEMI ClassicsProducerJohn FraserPaul McCartney chronology Run Devil Run(1999) Working Classical(1999) Liverpool Soun...

Cerro Datos generalesNombre Club Atlético CerroApodo(s) Villeros, Albicelestes, CerrensesFundación 1 de diciembre de 1922 (101 años)Colores Blanco y CelestePresidente Alfredo JaureguiverryEntrenador Ignacio PallasInstalacionesEstadio Luis TróccoliCapacidad 25 000 espectadores[1]Ubicación Av. Dr. Santín Carlos Rossi 4707, Montevideo, UruguayInauguración 22 de agosto de 1964 (59 años)Uniforme Titular Alternativo Última ...

シェラトン都ホテル東京Sheraton Miyako Hotel Tokyo ホテル概要正式名称 シェラトン都ホテル東京ホテルチェーン マリオット・インターナショナル都ホテルズ&リゾーツ運営 近鉄・都ホテルズ所有者 近畿日本鉄道前身 都ホテル東京→ラディソン都ホテル東京階数 地下2階 - 地上12階部屋数 484室開業 1979年(昭和54年)7月7日最寄駅 東京メトロ・都営地下鉄白金台駅最寄IC 首都...

Computer bus protocol This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Advanced eXtensible Interface – news · newspapers · books · scholar · JSTOR (April 2022) (Learn how and when to remove this message) This ar...


![{\displaystyle \left[{\begin{matrix}0&A\\A^{T}&0\end{matrix}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b04896754d39fbfcb50519550c82e74d77be67a)
