Гармонический ряд
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Baptis dewasa di Northolt Park Baptist Church, London Raya, Baptist Union of Great Britain, 2015. Baptis dewasa (Inggris: adult baptismcode: en is deprecated ) adalah praktik pembaptisan bagi orang-orang dewasa, atau setidaknya orang-orang yang dapat menyatakan imannya secara sadar dan mampu menggunakan akal budi, berbeda dengan praktik baptis bayi yang memberikan baptis kepada para bayi atau anak-anak yang masih belum mengerti dan sadar akan keimanan. Beberapa denominasi yang hanya memprakti...

Williams di pawai Occupy Wall Street pada 2012 Jumaane D. Williams (/dʒuˈmɑːni/ joo-MAH-nee; lahir 11 Mei 1976) adalah seorang politikus asal Amerika Serikat yang menjabat sebagai Advokat Publik New York City sejak 2019. Ia adalah anggota Partai Demokrat dan menyebut dirinya sendiri sebagai seorang sosialis demokrat.[1] Referensi ^ Day, Meagan. I Have No Problem Saying I'm a Democratic Socialist. jacobinmag.com. Diakses tanggal 1 March 2019. Pranala luar Wikimedia Commons me...
American professional football season 2023 Seattle Sea Dragons seasonOwnerAlpha Acquico, LLCGeneral managerJim HaslettHead coachJim HaslettHome fieldLumen FieldResultsRecord7–3Division place2nd XFL NorthPlayoff finishLost Division Finals (at DC Defenders) 21–37 ← 2020 Seattle Sea Dragons The 2023 Seattle Sea Dragons season was the second season for the Seattle Sea Dragons as a professional American football franchise. They played as charter members of the XFL, one of eight...

Code of conduct The Code of the U.S. Fighting Force is a code of conduct that is an ethics guide and a United States Department of Defense directive consisting of six articles to members of the United States Armed Forces, addressing how they should act in combat when they must evade capture, resist while a prisoner or escape from the enemy. It is considered an important part of U.S. military doctrine and tradition, but is not formal military law in the manner of the Uniform Code of Military J...

Ekosistem perairan adalah lingkungan yang terdiri dari komponen biotik dan abiotik serta didominasi oleh air sebagai habitat dari komponennya. Ada bagian dari ekosistem ini yang bukan perairan, tapi jumlahnya kecil. Ekosistem ini dihuni oleh beragam makhluk yang hidupnya di air ataupun di dua alam (air dan darat). Makhluk hidup ini bisa berupa binatang dan tumbuhan. Pada ekosistem ini cahaya matahari terbatas. hal ini karena sulitnya cahaya matahari menembus perairan. Sehingga perubahan suhu ...

1796 battle during the War of the First Coalition Battle of AmbergPart of the Rhine Campaign of the War of the First CoalitionDate24 August 1796LocationAmberg49°28′16″N 11°49′45″E / 49.4712°N 11.8291°E / 49.4712; 11.8291Result Austrian victoryBelligerents Republican France Habsburg monarchyCommanders and leaders Jean-Baptiste Jourdan Archduke Charles Wilhelm von WartenslebenStrength 34,000 40,000Casualties and losses 2,000 400class=notpageimage| Location wi...

Battle in the Uruguayan struggle for independence This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Battle of Las Piedras 1811 – news · newspapers · books · scholar · JSTOR (August 2014) (Learn how and when to remove this message) Battle of Las PiedrasPart of the Spanish American wars of independenceSurrender of Posadas at...

XEIMT-TDTKota Meksiko, MeksikoSaluranDigital: 23 (UHF)Virtual: 22 (PSIP)BrandingCanal 22Sloganel canal cultural de mexico (saluran budaya Meksiko)PemrogramanSubkanal22.1, 22.2 ATSCAfiliasiEdusatKepemilikanPemilikConaculta (Televisión Metropolitana)RiwayatDidirikan1982Makna tanda panggilXE Instituto Mexicano de la Televisión, mantan penyiaran publik (Imevisión)PranalaSitus webhttp://www.canal22.org.mx/ XEIMT-TDT (saluran 22) adalah sebuah stasiun televisi budaya dan pendidikan yang dimiliki...

Sports teams of Oakland University Oakland Golden GrizzliesUniversityOakland UniversityConferenceHorizon LeagueNCAADivision IAthletic directorSteve WaterfieldLocationRochester, MichiganVarsity teams16Basketball arenaAthletics Center O'renaBaseball stadiumOakland University Baseball FieldMascotGrizzNicknameGolden GrizzliesFight songOU FightColorsBlack and gold[1] Websitewww.goldengrizzlies.com The Oakland University Golden Grizzlies are the athletic teams tha...

Cadrezzate abolished municipality in ItalyFrazione Tempat Negara berdaulatItaliaRegion di ItaliaLombardyProvinsi di ItaliaProvinsi VareseKomune di ItaliaCadrezzate con Osmate Ibu kota dariCadrezzate con Osmate NegaraItalia Ibu kotaCadrezzate PendudukTotal1.842 (2018 )GeografiLuas wilayah4,73 km² [convert: unit tak dikenal]Ketinggian281 m Berbatasan denganAngera Ispra Osmate Sesto Calende Travedona-Monate Brebbia SejarahSanto pelindungMargareta dari Antiokhia Informasi tambahanKode...

Министерство природных ресурсов и экологии Российской Федерациисокращённо: Минприроды России Общая информация Страна Россия Юрисдикция Россия Дата создания 12 мая 2008 Предшественники Министерство природных ресурсов Российской Федерации (1996—1998)Министерство охраны...

La bella addormentata nel boscoAurora dorme sotto l'incantesimo della strega Malefica in una scena del filmTitolo originaleSleeping Beauty Lingua originaleinglese Paese di produzioneStati Uniti d'America Anno1959 Durata75 min Rapporto2,55:1 Genereanimazione, fantastico, musicale, sentimentale RegiaRegista supervisore: Clyde GeronimiRegisti sequenze: Eric Larson, Wolfgang Reitherman, Les Clark Soggettodalla fiaba di Charles Perraultstoria di Erdman Penner, Joe Rinaldi, Winston Hibl...

Concentration diagram of Cholera deaths 1854 in London (John Snow (1813-1858)) The defect concentration diagram (also problem concentration diagram[1]) is a graphical tool that is useful in analyzing the causes of the product or part defects.[2] It is a drawing of the product (or other item of interest), with all relevant views displayed, onto which the locations and frequencies of various defects are shown. Usage Defect concentration diagram is used effectively in the followi...

Penisola ibericaLa penisola iberica vista dal satellite. Stati Spagna Portogallo Andorra Francia Gibilterra Superficie596 759[1] km² Abitanti56 730 914 Densità95 ab./km² LingueSpagnolo, portoghese, catalano, basco, galiziano, dialetto aranese, inglese, francese Fusi orariUTC+0, UTC+1 Nome abitantiiberici La penisola iberica, anche conosciuta come Iberia, rappresenta l'estrema propaggine dell'Europa sud-occidentale; ha una superficie...

Irish song published in 1808 Believe Me, If All Those Endearing Young Charms Instrumental, United States Air Force Band of the Rockies, Stellar Brass, 2007 Problems playing this file? See media help. Believe Me, If All Those Endearing Young Charms is a popular song written by the Irish poet Thomas Moore, setting new lyrics to a traditional Irish air that can be traced back into the 18th century.[1] He published it in 1808, naming the air as My Lodging is on the Cold Ground from lyrics...

Shruti HaasanInformasi latar belakangNama lahirShruti Rajalakshmi HaasanLahir28 Januari 1986 (umur 38)Chennai, Tamil Nadu, GenrePop, R&B, dance, rockPekerjaanAktris, Penyanyi, Supermodel, Komposer, PenariTahun aktif2000–present Shruti Rajalakshmi Haasan (lahir 28 Januari 1986) adalah seorang Aktris, Penyanyi, Supermodel, Komposer, dan Penari kewarganegaraan India yang merupakan salah satu Aktris di industri perfilman Bollywood. Diskografi Judul Tahun Film Komposer Catatan Potri Paa...

2020年夏季奥林匹克运动会尼加拉瓜代表團尼加拉瓜国旗IOC編碼NCANOC尼加拉瓜奥林匹克委员会網站www.con.org.ni(西班牙文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員8參賽項目6个大项旗手开幕式:Sema Ludrick(举重)[1]闭幕式:东京奥组委志愿者[2]历届奥林匹克运动会参赛记录(总结)夏季�...
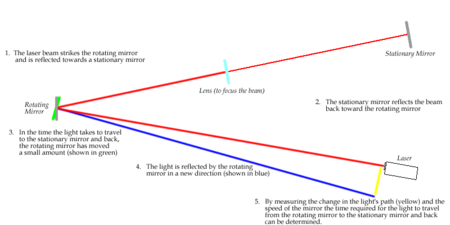
French physicist (1819–1868) Léon FoucaultPhotograph by Bertall & CieBornJean Bernard Léon Foucault18 September 1819Paris, FranceDied11 February 1868(1868-02-11) (aged 48)Paris, FranceResting placeMontmartre CemeteryAlma materUniversity of ParisKnown forFoucault knife-edge testFoucault pendulumFoucault's currentsFoucault's gyroscopeFoucault's measurements of the speed of lightGlan–Foucault prismDiurnal motionGyroscopeCatadioptric systemsSilvering processAwardsCopley M...

Questa voce o sezione sull'argomento personaggi di anime e manga non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Yuki Cross UniversoVampire Knight Nome orig.黒主優姫 Kuran (Yūki Kurosu) Lingua orig.Giapponese AutoreMatsuri Hino EditoreHakusensha 1ª app. in Manga: Volume 1 Anime: Episodio 1 Voce orig.Yui Horie Voce italianaBen...

2. Fußball-Bundesliga 1975-1976 Competizione 2. Fußball-Bundesliga Sport Calcio Edizione 2ª Organizzatore DFB Luogo Germania Ovest Partecipanti 40 Risultati Promozioni TeBe Berlino Saarbrücken Borussia Dortmund Retrocessioni Mülheim-Styrum Wacker 04 Berlino Gütersloh Spandauer Magonza Schweinfurt 05 Eintracht Bad Kreuznach Reutlingen Statistiche Miglior marcatore Norbert StolzenburgKarl-Heinz Granitza Incontri disputati...
















































































![{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363c98e0adc44d3ce15b51fdff0b28f7216a38f2)













