Ygos-Saint-Saturnin

Coordonate: 43°58′34″N 0°44′12″W ({{PAGENAME}}) / 43.97611°N 0.73667°V
Ygos-Saint-Saturnin
— Comună —

Ygos-Saint-Saturnin Ygos-Saint-Saturnin (Franța) Poziția geografică

Țară	Franța
Regiune	Nouvelle-Aquitaine
Departament	Landes


Suprafață^[2]
- Total	57,88 km²
Altitudine^[4]	101 m.d.m.

Populație (2009^[1])
- Total	1.187 locuitori
- Densitate	20,51 loc./km²

Fus orar	UTC+1
Cod poștal	40110
Cod INSEE	40333

Prezență online
site web oficial GeoNames OpenStreetMap relation

Poziția localității Ygos-Saint-Saturnin Poziția localității Ygos-Saint-Saturnin
Modifică date / text

Ygos-Saint-Saturnin este o comună în departamentul Landes din sud-vestul Franței. În 2009 avea o populație de 1.187 de locuitori.^[1]

Evoluția populației

Demografia în Ygos-Saint-Saturnin (Sursa : INSEE^[1])
An	1975	1982	1990	1999	2006	2009
Populație	1.420	1.282	1.207	1.131	1.091	1.187

Note

^ ^a ^b ^c „Populația comunelor din Landes”. Thomas Brinkhoff: City Population. Accesat în 17 august 2012.
^ „Suprafaţa comunelor din Franţa”. Toutes les villes. Accesat în 10 iulie 2012.
^ répertoire géographique des communes, accesat în 26 octombrie 2015
^ ^a ^b répertoire géographique des communes, 2015

Vezi și

Lista comunelor din Landes

Commons

Wikimedia Commons conține materiale multimedia legate de Ygos-Saint-Saturnin

Acest articol legat de o zonă sau o localitate din Franța este un ciot. Puteți ajuta Wikipedia prin completarea sa

v • d • m

Comunele din departamentul Landes

Read other articles:

Ikan soang

Ikan soang Sladenia shaefersi Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Actinopterygii Ordo: Lophiiformes Famili: LophiidaeRafinesque, 1810 Genus[1] Eosladenia (Punah) Lophiodes Lophiomus Lophius Sharfia (Punah) Sladenia Ikan soang adalah sebutan ikan sungut ganda (Lophiiformes) dalam keluarga Lophiidae. Ikan ini ditemukan di samudra yang ada di seluruh dunia. Mereka hidup di dasar lautan berpasir dan berlumpur di landas kontinen dan lereng benua hingga kedalaman l...

Johor Bahru

This article is about the city. For the district, see Johor Bahru District. For other uses, see Johor Bahru (disambiguation). Not to be confused with Johar Baru. State capital city and district capital in Johor, MalaysiaJohor BahruState capital city and district capitalCity of Johor BahruBandaraya Johor BahruOther transcription(s) • Jawiجوهر بهارو‎ • Chinese新山 (Simplified)新山 (Traditional)Xīnshān (Hanyu Pinyin) • Tamilஜொக�...

Hallyards Castle

Ruins of Halyards Castle Hallyards Castle (Scots: Hall yairds the yards at the hall),[1] located to the north-west of the village of Auchtertool, is reputed to have been a hunting seat of Malcolm Canmore.[2] With the establishment of the Roman Church, Halyards became the local residence of the Bishops of Dunkeld; it remained so until the first lay proprietor took possession in 1539. The influence that Halyards had on the district cannot be overstated. When Sir James Kirkcaldy...

Schwaben Baru

Peta lokasi Swabia Baru. Schwaben Baru atau Swabia Baru (Jerman: Neuschwabenland) adalah bagian di benua Antarktika antara 20°E dan 10°W (melebihi klaim teritori Norwegia atas Daratan Ratu Maud), yang diklaim oleh Jerman Nazi antara 19 Januari 1939 hingga 8 Mei 1945. Wilayah ini dinamai dari wilayah Swabia di Jerman. Pranala luar 1901–03 German Antarctic Expedition Scott Polar Research Institute 1911–12 German Antarctic Expedition Scott Polar Research Institute Secret Mission to the Ant...

Retard (musique)

Pour les articles homonymes, voir Retard. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (septembre 2007). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique&#...

National Register of Historic Places listings in Staunton, Virginia

Location of Staunton in Virginia This is a list of the National Register of Historic Places listings in Staunton, Virginia. This is intended to be a complete list of the properties and districts on the National Register of Historic Places in the independent city of Staunton, Virginia, United States. The locations of National Register properties and districts for which the latitude and longitude coordinates are included below, may be seen in an online map.[1] There are 35 properties a...

Piotta (Quinto)

Piottafrazione Piotta – Veduta LocalizzazioneStato Svizzera Cantone Ticino DistrettoLeventina ComuneQuinto TerritorioCoordinate46°30′46″N 8°40′35″E / 46.512778°N 8.676389°E46.512778; 8.676389 (Piotta)Coordinate: 46°30′46″N 8°40′35″E / 46.512778°N 8.676389°E46.512778; 8.676389 (Piotta) Altitudine1 006 m s.l.m. Abitanti200 circa (-) Altre informazioniCod. postale6776 Prefisso091 Fuso orarioUTC+1 TargaTI ...

Serra dos Aimorés

Questa voce sull'argomento centri abitati del Minas Gerais è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Serra dos Aimoréscomune Serra dos Aimorés – Veduta LocalizzazioneStato Brasile Stato federato Minas Gerais MesoregioneVale do Mucuri MicroregioneNanuque AmministrazioneSindacoAgripino Botelho Barreto TerritorioCoordinate17°47′01″S 40°14′41″W / 17.783611°S 40...

Soya Bus

Perusahaan bus Soya (soya bus) adalah perusahaan bus Jepang yang berkantor pusat di Wakkanai, Hokkaido, Jepang. Sōya bus S230A 0662 Ringkasan Soya Bus adalah sebuah perusahaan bus yang melayani daerah-daerah di bagian paling utara di negara Jepang atau lebih tepatnya di Subprefektur Sōya, Hokkaido, Jepang, terutama di Wakkanai, Rishiri, Rishirifuji, dan Rebun. Jalur Wakkanai 1: Shiomi Blok 5 -Stasiun Minami-Wakkanai - Minato Blok 3 - Stasiun Wakkanai - SMP Wakkanai - Noshappu. 2: Noshappu -...

美国众议院

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目，无法查证的内容可能會因為异议提出而被移除。致使用者：请搜索一下条目的标题（来源搜索：美国众议院 — 网页、新闻、书籍、学术、图像），以检查网络上是否存在该主题的更多可靠来源（判定指引）。美國眾議院 United States House of Representatives第118届美国国会众议院徽章众议院旗...

سعد الدين التفتازاني

سعد الدين التفتازاني معلومات شخصية الميلاد 1322م - 722هـخراسان الكبرى الوفاة 1390م - 792هـسمرقند مكان الدفن سمرقند، وسرخس الإقامة سرخس مواطنة الدولة التيمورية[1] الديانة الإسلام، أهل السنة والجماعة، شافعية، حنفية، أشعرية، ماتريدية الحياة العملية تعلم لدى عضد ا...

Metal Arms: Glitch in the System

2003 video gameMetal Arms: Glitch in the SystemNorth American PS2 cover artDeveloper(s)Swingin' Ape StudiosMass Media Inc. (PlayStation 2)Publisher(s)Vivendi Universal Games[a]Director(s)Dave WittenbergKeith AremWriter(s)Dave WittenbergKeith AremComposer(s)Keith AremPlatform(s)GameCube, PlayStation 2, XboxReleaseNA: November 18, 2003PAL: December 5, 2003Genre(s)Third-person shooter, action-adventureMode(s)Single-player, multiplayer Metal Arms: Glitch in the System is a third-person sh...

Vladyslav Ohirya

Ukrainian footballer Vladyslav Ohirya Personal informationFull name Vladyslav Leonidovych OhiryaDate of birth (1990-04-03) 3 April 1990 (age 34)Place of birth Hirske, Ukrainian SSRHeight 1.75 m (5 ft 9 in)Position(s) MidfielderTeam informationCurrent team Polissya ZhytomyrNumber 8Youth career FC Shakhtar Hirske2003–2007 LVUFK LuhanskSenior career*Years Team Apps (Gls)2007–2013 Zorya Luhansk 3 (0)2010–2011 → Arsenal Bila Tserkva (loan) 28 (2)2011–2013 → Olimpik ...

A. A. Ames

American politician (1842–1911) Doc Amesc. 1897Mayor of MinneapolisIn officeJanuary 7, 1901 – August 27, 1902Preceded byJames GraySucceeded byDavid P. JonesIn officeApril 13, 1886 – January 7, 1889Preceded byGeorge A. PillsburySucceeded byEdward C. BabbIn officeApril 11, 1882 – April 8, 1884Preceded byAlonzo Cooper RandSucceeded byGeorge A. PillsburyIn officeApril 11, 1876 – April 10, 1877Preceded byOrlando C. MerrimanSucceeded byJohn De LaittreMe...

Nordic Opening 2011-2012

Nordic Opening 2011-12 Généralités Sport Ski de fond Organisateur(s) Fédération internationale de ski Éditions 2e Lieu(x) Europe du Nord Date 25 novembre 2011 au27 novembre 2011 Épreuves 3 Site web officiel http://www.nordicopening.com/en/ Palmarès Vainqueur Navigation 2010 2012 modifier La 2e édition du Nordic Opening s'est déroulée du 25 novembre 2011 au 27 novembre 2011. Cette compétition est intégrée à la coupe du monde de ski de fond 2011-2012 et est organisée par l...

Allyn Abbott Young

American economist (1876-1929) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Allyn Abbott Young – news · newspapers · books · scholar · JSTOR (March 2024) (Learn how and when to remove this message) Allyn Abbott YoungBornSeptember 19, 1876Kenton, Ohio, U.S.DiedMarch 7, 1929 (1929-03-08) (aged 52)...

جورج ميلر (مخرج)

لمعانٍ أخرى، طالع جورج ميلر (توضيح). جورج ميلر (بالإنجليزية: George Miller)‏ معلومات شخصية الميلاد 3 مارس 1945 (العمر 79 سنة)بريزبان مواطنة أستراليا مناصب رئيس لجنة التحكيم في مهرجان كان السينمائي الأخوان كوين بيدرو ألمودوبار الحياة العملية المدرسة الأم جامعة...

Camp Williams

Camp WilliamsPrésentationType Centre de formation militaireFondation 1928Gestionnaire Utah Army National Guard (en)Site web ut.ng.milLocalisationLocalisation Comté d'Utah, comté de Salt Lake, Utah 84065 États-UnisAltitude 1 464 mMassif Monts TraverseCoordonnées 40° 26′ 15″ N, 111° 55′ 32″ Omodifier - modifier le code - modifier Wikidata Camp W. G. Williams, communément appelé Camp Williams, connu aussi sous le nom Army Garrison Camp Wil...

NCT 2018 Empathy

『NCT 2018 Empathy』NCT のスタジオ・アルバムリリース 2018年3月14日ジャンル K-POP時間 44分レーベル Dreamusチャート最高順位ガオンチャート週間2位[1] 月間3位[2] 年間13位[3]ゴールドディスクダブルプラチナ（ガオンチャート）NCT アルバム年表 NCT 2018 Empathy（2018年）NCT 2020 RESONANCE Pt. 1（2020年）テンプレートを表示『NCT 2018 Empathy』（エヌシーティー二ゼロ�...

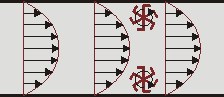
Rotacional

En el cálculo vectorial, el rotacional o rotor es un operador vectorial sobre campos vectoriales definidos en un abierto de R 3 {\displaystyle \mathbb {R} ^{3}} que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto: U ⋅ rot F = U ⋅ ∇ × F ≡ lim Δ S →...