Spațiu Banach
|
Read other articles:

Allal al-FassiAllal al-Fassi tahun 1956Lahir10 Januari 1910Fez, MorokoMeninggal13 Mei 1974(1974-05-13) (umur 64)Bukares, RomaniaPartai politikIstiqlal Allal bin Abdul Wahid bin Abdus Salam bin Allal al-Fassi al-Fahri (Arab: علال بن عبد الواحد بن عبد السلام بن علال الفاسي الفهريcode: ar is deprecated , 10 Januari 1910 – 13 Mei 1974) adalah seorang politisi, pengarang, penulis puisi, dan ilmuwan Islam dari Maroko.[1] Poli...

For other uses, see KHFX (disambiguation). Radio station in Cleburne, TexasKHFXCleburne, TexasBroadcast areaDallas-Fort Worth MetroplexFrequency1140 kHzBrandingRadio Pentecostes Cristo Vive 1140ProgrammingFormatSpanish language Christian radioOwnershipOwnerSiga Broadcasting CorporationSister stationsKFJZHistoryFirst air date1947 on 1120Former call signsKCLE (1947-2008)Technical informationFacility ID65313ClassBPower5,000 watts (day)710 watts (night)LinksWebsiteSiga Broadcasting Website KHFX (...

Vijay KumarShri Pranab Mukherjee mempersembahkan Padma Shri Award kepada Shri Vijay Kumar, pada Upacara Penobatan-II, pada 20 April 2013Informasi pribadiKewarganegaraanIndiaLahir19 Agustus 1985 (umur 38)Harsour, HamirpurHimachal Pradesh, India OlahragaNegaraIndiaOlahragaMenembak Rekam medali Permainan Olimpiade {{{3}}} 2012 London Pistol api cepat 25 m Kejuaraan Menembak Dunia ISSF {{{3}}} 2009 Beijing 25m Rapid Fire Pistol 2011 Fort Benning Pistol Api Cepat 25m Commonwealth ...

Motor rifle division of the Soviet military 71st Motor Rifle DivisionActive1984–1989Country Soviet UnionBranch Soviet ArmyGarrison/HQSemipalatinskMilitary unit The 71st Motor Rifle Division (Military Unit Number 07225) was a motorized infantry division of the Soviet Army between 1984 and 1989. It was based in Semipalatinsk. Converted to a storage base in 1989, it was taken over by Kazakhstan with the dissolution of the Soviet Union.[1] History The 71st Motor Rifle Division...

Archaeological site in Afghanistan Hadda(Afghanistan)Buddhist stupas at Hadda, by William Simpson, 1881.[1]Shown within AfghanistanShow map of AfghanistanHadda, Afghanistan (Gandhara)Show map of GandharaHadda, Afghanistan (South Asia)Show map of South AsiaCoordinates34°21′42″N 70°28′15″E / 34.361685°N 70.470752°E / 34.361685; 70.470752TypeGroup of Buddhist monasteriesHistoryFounded1st century BCEAbandoned9th century CE Haḍḍa (Pashto: هډه) is ...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...
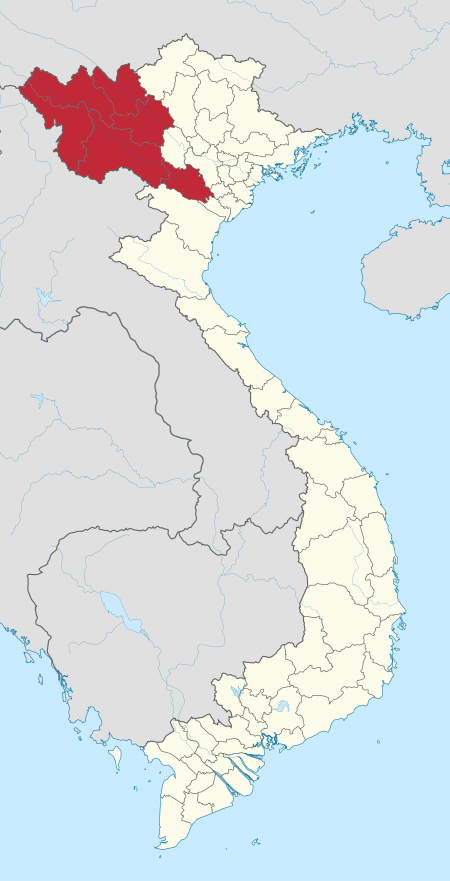
District in Northwest, VietnamSốp Cộp District Huyện Sốp CộpDistrictCountry VietnamRegionNorthwestProvinceSơn LaCapitalSốp CộpArea • Total570 sq mi (1,477 km2)Population (2003) • Total32,253Time zoneUTC+7 (UTC + 7) Sốp Cộp is a rural district of Sơn La province in the Northwest region of Vietnam. It was established in December 2003. As of 2003, the district had a population of 32,253.[1] The district covers an area o...

1986 studio album by Wendy CarlosBeauty in the BeastStudio album by Wendy CarlosReleased1986 (1986)Genre Classical electronic experimental Length57:41LabelAudion RecordsProducerWendy CarlosWendy Carlos chronology Digital Moonscapes(1984) Beauty in the Beast(1986) Wendy Carlos: Secrets of Synthesis(1990) Beauty in the Beast is a studio album from the American keyboardist and composer Wendy Carlos, released in 1986, on Audion Records, her first for a label other than Columbia Recor...

Maladie cœliaque diagramme de l'intestin grêle supérieur montrant la maladie cœliaque : atrophie des villosités, hyperplasie des cryptes et infiltration lymphocytaire des cryptes. Données clés Symptômes Diarrhée, constipation, vomissement et nausée Traitement Spécialité Gastro-entérologie Classification et ressources externes CISP-2 D99 CIM-10 K90.0 OMIM 612008, 612005, 612006, 607202, 611598, 612007, 612011 et 612009 609754, 612008, 612005, 612006, 607202, 611598, 612007, ...

Postseason college football game This article is about the FCS (Division I-AA) championship game. For the FBS (Division I-A) championship game, see 2020 College Football Playoff National Championship. College football game2020 NCAA Division I Football ChampionshipFCS National Championship Game James Madison Dukes North Dakota State Bison (14–1) (15–0) CAA MVFC 20 28 Head coach: Curt Cignetti Head coach: Matt Entz STATSSeed 22 STATSSeed 11 1234 Total James Madison 7337 ...

Halaman ini berisi artikel tentang kelompok etnik Slavic Timur. Untuk semua warga negara Rusia, lihat Demografi Rusia dan Hukum kewarganegaraan Rusia. Orang Rusiabahasa Rusia: русскиеJumlah populasic. 135 juta [butuh rujukan]Daerah dengan populasi signifikan Russia 105.620.179 (2021)[1]DiasporaJermansekitar 7.500.000 (termasuk Yahudi Rusia dan Jerman Rusia)[2][3][4]Ukraina7.170.000 (2018) (termasuk Krimea)[5]Kazakhst...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (mard 2020). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Canal Charleroi-Bruxelles Localisation du canal Charl...

ДеревняБельское Устье 57°40′42″ с. ш. 29°42′16″ в. д.HGЯO Страна Россия Субъект Федерации Псковская область Муниципальный район Порховский Сельское поселение Красноармейская волость История и география Прежние названия Знаменка Часовой пояс UTC+3:00 Население На�...

Loris DamonteNazionalità Italia Altezza191 cm Peso85 kg Calcio RuoloCentrocampista, difensore SquadraVoltrese Vultur CarrieraGiovanili Genoa Squadre di club1 2007-2008 Genoa0 (0)2008-2011→ Alessandria46 (6)[1]2011-2014 Varese68 (4)[2]2014-2015→ Messina33 (2)[3]2015-2016 Pistoiese26 (1)2016-2018 Sambenedettese36 (1)[4]2018 Gavorrano16 (3)[5]2018-2019 Albissola23 (2)2019-2021 Renate56 (0)[...

Lambang negara pertama Rusia Soviet Konstitusi Konstitusi pertama Rusia, juga disebut Hukum Dasar (Основной закон, Osnovnoy zakon) yang mengatur Republik Soviet Federatif Sosialis Rusia, menjelaskan rezim yang merebut kekuasaan dalam Revolusi Oktober 1917. Konstitusi tersebut, yang diratifikasi tak lama setelah Deklarasi Hak Tenaga Kerja dan Orang yang Tereksploitasi,[1] resmi mengakui kelas tenaga kerja sebagai kelas pemerintahan Rusia menurut prinsip kediktatoran prolet...

Ancient port and city in Tel Aviv, Israel For other uses, see Jaffa (disambiguation). Aerial view of old Jaffa Aerial view of old Jaffa and port with Tel Aviv behind Jaffa (Hebrew: יָפוֹ, romanized: Yāfō, pronounced [jaˈfo] ⓘ; Arabic: يَافَا, romanized: Yāfā, pronounced [ˈjaːfaː]), also called Japho or Joppa in English, is an ancient Levantine port city which is part of Tel Aviv-Yafo, Israel, located in its southern part. The city sits atop a nat...

British engineer (1851–1928) SirHorace DarwinKBE FRSPhotograph of Horace DarwinBorn13 May 1851Downe, England, United Kingdom of Great Britain and IrelandDied22 September 1928(1928-09-22) (aged 77)SpouseEmma Cecilia Ida FarrerChildrenErasmus Darwin IV Ruth Frances Darwin Nora BarlowParent(s)Charles Darwin and Emma Darwin Sir Horace Darwin, KBE FRS (13 May 1851 – 22 September 1928) was an English engineer specializing in the design and manufacture of precision scientific instru...

This is an archive of past discussions. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. Archives 2023;Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2022;Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2021;Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2020;Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2019;Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec 2018;Jan Feb Mar Apr May Jun Jul Aug Sep Oct ...

2017 European windstorm Not to be confused with Cyclone Xaver. For other storms of the same name, see Tropical Storm Xavier. Cyclone XavierAqua Modis satellite view of Xavier crossing Germany and Poland on 5 October 2017. TypeEuropean windstormFormed4 October 2017Dissipated6 October 2017 Highest gust202 km/h (126 mph), (Mountain value) Sněžka, Czech Republic[1]Beaufort scale10–12Lowest pressure985[2] mb (29.09 inHg) Fatalities9 (7 Germany, 2 Poland)[...

Ne doit pas être confondu avec Luc Chatel (journaliste). Luc Chatel Luc Chatel en 2015. Fonctions Député français 20 juin 2012 – 20 juin 2017(5 ans) Élection 10 juin 2012 Circonscription 1re de la Haute-Marne Législature XIVe (Cinquième République) Groupe politique UMP (2012-2015)LR (2015-2017) Prédécesseur Sophie Delong Successeur Bérangère Abba 19 juin 2002 – 19 juillet 2007(5 ans et 1 mois) Élection 16 juin 2002 Réélection 10 juin 2007 Circonscription 1re...


























































































