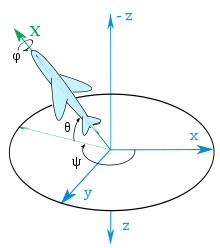
Orientare (geometrie)
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Fanny CadeoLahirStefania Cadeo11 September 1970 (umur 53)Lavagna, ItaliaKebangsaanItaliaPekerjaan Aktris penyanyi model Tahun aktif1992–sekarangTinggi170 cm (5 ft 7 in)Suami/istriStefano Caviglia (m.&#...

American Civil War soldier Henry Hoʻolulu PitmanPortrait of Henry Hoʻolulu Pitman at the Peabody Essex Museum[1]Born(1845-03-18)March 18, 1845Hilo, Hawaiʻi, Kingdom of HawaiʻiDiedFebruary 27, 1863(1863-02-27) (aged 17)Camp Parole, Annapolis, MarylandBuriedMount Auburn Cemetery, Cambridge, MassachusettsAllegianceUnited States of AmericaUnionService/branchUnion ArmyYears of service1862–1863RankPrivateUnit22nd Regiment Massachusetts Volunteer InfantryBattles/warsAmerican ...

BakpiaAsalNegara asalRepublik Rakyat Tiongkok dan Indonesia Keahlian memasakhidangan Tionghoa Filipina, masakan Indonesia dan Masakan Jawa RincianJenisPastri, makanan dan camilan Metode penyajianpanggang dan Kukus Bahan utamatepung terigu, gula, margarin, Kacang hijau, Sari kelapa, pandan wangi, vanili, kuning telur, Tepung jagung, minyak sayur, Kacang hitam, Kacang azuki dan cokelat lbs Bakpia Asli Tradisional Otentik Bakpia (Hanzi: 肉餅; Pe̍h-ōe-jī: bah-piáⁿ; harfiah: 'k...

Yohanes 20Yohanes 16:14-22 pada sisi recto dari Papirus 5, yang ditulis sekitar tahun 250 M.KitabInjil YohanesKategoriInjilBagian Alkitab KristenPerjanjian BaruUrutan dalamKitab Kristen4← pasal 19 pasal 21 → Yohanes 20 (disingkat Yoh 20) adalah bagian Injil Yohanes pada Perjanjian Baru dalam Alkitab Kristen, menurut kesaksian Yohanes, salah seorang dari dua belas murid utama Yesus Kristus.[1][2] Teks Naskah aslinya ditulis dalam bahasa Yunani. Salah satu naskah kun...

Stefan Stambolov Stefan Stambolov adalah seorang politikus asal Bulgaria. Ia menjabat sebagai kepala pemerintahan untuk Kepangeranan Bulgaria selama periode tahun 1887–1894 M.[1] Referensi ^ Eni, S. P., dan Tsabit, A. H. (2014). Arsitektur Kuno Bulgaria di Eropa Timur: Sejarah, Kebudayaan, Arkeologi (PDF). Jakarta: Rajawali Press. hlm. 23. ISBN 978-979-769-809-6. Parameter |url-status= yang tidak diketahui akan diabaikan (bantuan)Pemeliharaan CS1: Banyak nama: a...

Letak Palung Jepang Palung Jepang adalah sebuah palung yang merupakan bagian dari Cincin Api Pasifik, terletak di dasar Samudra Pasifik bagian utara, tepatnya di sebelah timur laut Jepang. Palung berkedalaman terdalam 9.000 meter, memanjang dari Kepulauan Kuril hingga Kepulauan Bonin. Kapal selam penelitian Shinkai-6500 yang berawak 3 orang pada 11 Agustus 1989 berhasil menyelam di palung ini sampai kedalaman 6.526 meter. 34°N 142°E / 34°N 142°E / 34; 142 Artikel b...

Distrik Mannar(Mannar District) மன்னார் மாவட்டம்මන්නාරම දිස්ත්රික්කයadministratif distrikLokasi di Sri LankaDS dan Divisi GN dari Distrik Mannar, tahun 2006Koordinat: 08°52′N 80°04′E / 8.867°N 80.067°E / 8.867; 80.067Koordinat: 08°52′N 80°04′E / 8.867°N 80.067°E / 8.867; 80.067NegaraSri LankaProvinsiUtaraIbukotaMannarDivisi DS Daftar MadhuMannarManthai BaratMu...

Cet article est une ébauche concernant le Concours Eurovision de la chanson et Saint-Marin. Vous pouvez partager vos connaissances en l’améliorant (comment ?) ; pour plus d’indications, visitez le projet Eurovision. Saint-Marinau Concours Eurovision 2015 Données clés Pays Saint-Marin Chanson Chain of Light Interprète Michele Perniola et Anita Simoncini Langue Anglais Sélection nationale Type de sélection Sélection interne Date 27 novembre 2014 (artistes)16 mars 20...

Election in Ohio Main article: 2016 United States presidential election 2016 United States presidential election in Ohio ← 2012 November 8, 2016 2020 → Turnout66.48% [1] Nominee Donald Trump Hillary Clinton Party Republican Democratic Home state New York New York Running mate Mike Pence Tim Kaine Electoral vote 18 0 Popular vote 2,841,005 2,394,164 Percentage 51.31% 43.24% County results Congressional district results Precinct results T...

Building in New Jersey, United StatesThe Empress HotelGeneral informationLocation101 Asbury Avenue, Asbury Park, New Jersey, United States 07712Opening1961OwnerShep PettiboneTechnical detailsFloor count4Other informationNumber of rooms101Number of restaurants1WebsiteOfficial Website The Empress Hotel is a popular gay resort located in Asbury Park, New Jersey.[1] The Hotel opened as a luxury resort for vacationing families in the 1960s.[2] It was a successful resort, attractin...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Occupazione italiana di Maiorca (dettagli) (dettagli) Occupazione italiana di Maiorca - Localizzazione Dati amministrativiLingue ufficialiItaliano Lingue parlateCastigliano, catalano CapitalePalma di Maiorca Dipendente da Italia PoliticaForma di StatoAmministrazione militare Nascita1936 con Arconovaldo Bonacorsi CausaBattaglia di Maiorca (Guerra civile spagnola) Fine1939 CausaRitiro delle truppe italiane dalla Spagna Territorio e popolazioneBacino geograficoMar Mediterraneo EconomiaComme...

Ocean's ElevenSutradaraSteven SoderberghProduserJerry WeintraubDitulis olehGeorge C. JohnsonJack G. RussellHarry BrownCharles LedererScott CorwonTed GriffinPemeranGeorge ClooneyBrad PittMatt DamonAndy GarciaJulia RobertsDistributorWarner Bros.Tanggal rilis5 Desember 2001Durasi116 menitAnggaran$85,000,000 Ocean's Eleven merupakan sebuah film yang diproduksi oleh Warner Bros dengan sutradara Steven Soderbergh. Film yang dirilis pada tahun 2001 ini merupakan versi remake dari film dengan judul y...

State Park in Washington, United States Leadbetter Point State ParkEntrance signLocation in the state of WashingtonShow map of Washington (state)Leadbetter Point State Park (the United States)Show map of the United StatesLocationPacific, Washington, United StatesCoordinates46°35′49″N 124°03′13″W / 46.59694°N 124.05361°W / 46.59694; -124.05361[1]Area1,732 acres (7.01 km2)Elevation43 ft (13 m)[1]Established1974[2]Operato...

American author, critic, and academic (born 1942) Samuel R. DelanySamuel R. Delany in 2022BornSamuel Ray Delany Jr. (1942-04-01) April 1, 1942 (age 82)Harlem, New York City, U.S.Pen nameK. Leslie Steiner, S. L. KermitOccupation Writer editor professor literary critic EducationCity College of New YorkPeriod1962–present[1]GenreScience fiction, fantasy, autobiography, creative nonfiction, erotic literature, literary criticismSubjectScience fiction, lesbian and gay studies, erotici...
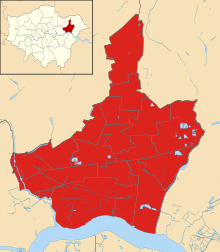
2022 local election in Barking and Dagenham 2022 Barking and Dagenham Council election ← 2018 5 May 2022 2026 → All 51 council seats First party Lab Leader Darren Rodwell Party Labour Leader since 17 May 2014 Last election 51 seats, 74.4% Seats won 51 Seat change Map of the results of the 2022 Barking and Dagenham council election. Labour in red. council control before election Labour Subsequent council control Labour The 2022 Barking an...

American singer and actress (1963–2012) For the album, see Whitney Houston (album). Not to be confused with Whitney Chewston. Whitney HoustonHouston at the Welcome Home Heroes concert in 1991BornWhitney Elizabeth Houston(1963-08-09)August 9, 1963Newark, New Jersey, U.S.DiedFebruary 11, 2012(2012-02-11) (aged 48)Beverly Hills, California, U.S.Burial placeFairview Cemetery, Westfield, New JerseyEducationMount Saint Dominic AcademyOccupationsSingeractressmodelfilm producerrecord producerp...

2016 EuropeanAthletics ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 mmenwomen10,000 mmenwomen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmenwomen3000 msteeplechasemenwomen4 × 100 m relaymenwomen4 × 400 m relaymenwomenRoad eventsHalf marathonmenwomenField eventsHigh jumpmenwomenPole vaultmenwomenLong jumpmenwomenTriple jumpmenwomenShot putmenwomenDiscus throwmenwomenHammer throwmenwomenJavelin throwmenwomenCombined eventsHeptathlonwomenD...

Russian politician Ivan IndinokИван Индинок2nd Head of Administration of Novosibirsk OblastIn office5 October 1993 – 13 December 1995Preceded byVitaly MukhaSucceeded byVitaly Mukha1st Mayor of NovosibirskIn office26 November 1991 – 5 October 1993Succeeded byViktor Tolokonsky Personal detailsBornIvan Ivanovich Indinok (1938-08-06) 6 August 1938 (age 86)Kozlovka [ru], Krasnoyarsk Krai, Russia, Soviet UnionPolitical partyOur Home - RussiaParentI...
Cet article est une ébauche concernant le Canada et le sport. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article n’est pas rédigé dans un style encyclopédique (février 2014). Vous pouvez améliorer sa rédaction ! Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'a...