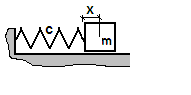
Mecanică lagrangiană
|
Read other articles:

Samos International Airport Aristarchos of SamosΚρατικός Αερολιμένας Σάμου «Αρίσταρχος ο Σάμιος»IATA: SMIICAO: LGSM SMILocation of airport in GreeceInformasiLokasiSamos Island, GreeceKetinggian dpl6 mdplKoordinat37°41′24″N 026°54′42″E / 37.69000°N 26.91167°E / 37.69000; 26.91167Koordinat: 37°41′24″N 026°54′42″E / 37.69000°N 26.91167°E / 37.69000; 26.91167Landasan pacu A...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juin 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? Comme...

علم الاتحاد الغربي الاستعمال راية الشعب علم (راية) التناسب 2:3 الاعتماد 1949 التصميم سلسلة غير منقطعة من خمسة روابط مستطيلة على شكل خماسي مقلوب على حقل أزرق، مع إطار متعدد الألوان (أحمر من الخارج، ذهبي، أسود وأبيض) تعديل مصدري - تعديل كان الاتحاد الغربي تحالفًا عسكريًا تم إ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Disambiguazione – Schiller rimanda qui. Se stai cercando altri significati, vedi Schiller (disambigua). Schiller ritratto da Gerhard von Kügelgen. Johann Christoph Friedrich von Schiller (/'jo:han 'kʀɪstɔf 'fʀi:dʀɪç fɔn 'ʃɪlɐ/, pronuncia tedesca ascoltaⓘ) (Marbach am Neckar, 10 novembre 1759 – Weimar, 9 maggio 1805) è stato un poeta, filosofo, drammaturgo, medico e storico tedesco. Indice 1 Biografia 1.1 Anni giovanili (1759-1775) 1.1.1 La famiglia 1.1.2 L'educazio...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 ...
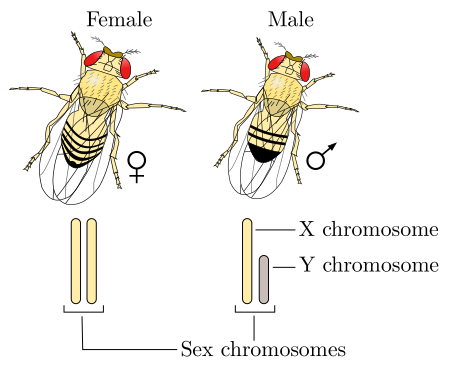
Kromosom seks Drosophila. Sistem penentuan kelamin XY adalah sistem penentuan kelamin yang dapat ditemui pada mamalia (termasuk manusia) dan beberapa serangga (Drosophila) serta beberapa tumbuhan (Ginkgo). Pada sistem penentuan seks XY, betina memiliki dua dari kromosom seks yang sama jenisnya (XX) dan disebut kelamin homogenik, sedangkan jantan memiliki dua kromosom seks berbeda (XY) dan disebut kelamin heterogenik. Sistem ini pertama kali dijelaskan oleh Nettie Stevens dan Edmund Beecher Wi...

1966 studio album by The Dave Clark FiveSatisfied with YouStudio album by The Dave Clark FiveReleased15 August 1966[1]GenrePop rock, beatLength21:17LabelEpicLN 24212 / BN 26212ProducerDave ClarkThe Dave Clark Five US chronology Try Too Hard(1966) Satisfied with You(1966) 5 by 5(1967) Singles from Try Too Hard Look Before You Leap / Please Tell Me WhyReleased: 20 May 1966[1] Satisfied with You / Don't Let Me DownReleased: 22 July 1966[1] Satisfied with You is th...

Wakil Gubernur Kalimantan TengahLambang provinsiPetahanaEdy Pratowosejak 25 Mei 2021Dibentuk1961Pejabat pertamaReinout SylvanusSitus webkalteng.go.id Inilah daftar Wakil Gubernur Kalimantan Tengah. No Foto Wakil Gubernur[1] Mulai Jabatan Akhir Jabatan Prd. Keterangan Gubernur 1 Reinout Sylvanus 1961 Februari 1967 2 Tjilik Riwut Tidak ada Februari 1967 3 Oktober 1978 3 Reinout Sylvanus 3 Oktober 1978 7 Oktober 1983 4 Willy Ananias Gara 7 Oktober 1983 23 Januari 1984 Eddy Sabara(Pe...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Noboru NakayamaInformasi pribadiNama lengkap Noboru NakayamaTanggal lahir 7 Juli 1987 (umur 36)Tempat lahir Prefektur Osaka, JepangPosisi bermain GelandangKarier senior*Tahun Tim Tampil (Gol)2006-2008 Cerezo Osaka * Penampilan dan gol di klub senior...

Ottoman Empire from circa 1450 to 1570 Part of a series on the History of theOttoman Empire Timeline Rise (1299–1453) Beylik of Osman Interregnum (1402–1413) Fall of Constantinople Classical Age (1453–1566) Sultanate of Women (1533–1656) Transformation (1566–1703) Köprülü Era (1656–1703) Old Regime (1703–1789) Tulip Era (1718–1730) Decline & Modernization (1789–1908) Nizam-i Djedid (late 18th and early 19th) Tanzimat Era (1839–...

Japanese-owned food company Fyffes plcCompany typePrivateIndustryProduceFounded1888 in London, United KingdomFounderEdward Wathen FyffeHeadquartersGeneva, SwitzerlandKey peopleHelge H. Sparsø CEOProductsFruit: bananas, melons, pineapples,Revenue€1.09 billion (2014)[1]Operating income€38.8 million (2014)[1]Net income€34.1 million (2014)[1]OwnerSumitomo Group (Japan)Websitewww.fyffes.com Fyffes plc (/faɪfs/ FYFS) is a fruit and fresh produce company. The Fyffes b...

Yayasan LontarJenisOrganisasi nirlabaPendiriGoenawan Susatyo MohamadSapardi Djoko DamonoUmar KayamSubagio SastrowardoyoJohn H. McGlynnKantorpusatJl. Danau Laut Tawar No. 53, Pejompongan, Jakarta 10210 IndonesiaWilayah operasiDuniaSitus webhttp://www.lontar.org/ Yayasan Lontar adalah organisasi independen dan nirlaba yang berkedudukan di Jakarta, Indonesia. Tujuan utama Lontar adalah untuk mempromosikan sastra dan budaya Indonesia melalui penerjemahan karya-karya sastra Indonesia dengan sasara...

Reptile genus of herbivorous lizards This article is about the genus. For the best known species, see Green iguana. For the family of related lizards, see Iguanidae. For other uses, see Iguana (disambiguation). IguanaTemporal range: Holocene–Recent[1][2] PreꞒ Ꞓ O S D C P T J K Pg N ↓ A green iguana (Iguana iguana) Conservation status CITES Appendix II (CITES)[3] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Repti...

Dieser Artikel behandelt die türkische Sprache im engeren Sinne. Zur Sprachfamilie Türkische Sprachen siehe Turksprachen. Türkisch (Türkçe) Gesprochen in Bosnien und Herzegowina Bosnien und HerzegowinaBulgarien BulgarienGeorgien GeorgienGriechenland GriechenlandIrak IrakKosovo KosovoLibanon LibanonNordmazedonien NordmazedonienRumänien RumänienSyrien SyrienTurkei TürkeiNordzypern Türkische Republik NordzypernZypern Republik&...

Not to be confused with Conservative Party of Georgia. Political party in Georgia (country) Conservative Movement/Alt Info კონსერვატიული მოძრაობა/ალტ ინფოChairmanGiorgi KardavaGeneral SecretaryShota MartinenkoFounderZurab MakharadzeGiorgi KardavaIrakli MartinenkoShota MartinenkoKonstantine MorgoshiaFounded20 November 2021 (2021-11-20)Registered7 December 2021 (2021-12-07)Dissolved11 April 2024&...

City in Northern Ireland For other uses, see Armagh (disambiguation). Human settlement in Northern IrelandArmaghIrish: Ard Mhacha[1]Scots: Airmagh[2]St Patrick's Cathedral, ArmaghLocation within Northern IrelandPopulation16,310 (2021 Census)Irish grid referenceH876455• Belfast33 mi (53 km)DistrictArmagh City, Banbridge and CraigavonCountyCounty ArmaghCountryNorthern IrelandSovereign stateUnited KingdomPost townARMAGHPostcode districtBT...

High cross from the 10th century West-face of Muiredach's High Cross. Muiredach's High Cross is a high cross from the 10th or possibly 9th century, located at the ruined monastic site of Monasterboice, in County Louth, Ireland. There are two other high crosses at Monasterboice; in local terms Muiredach's cross is also known as the South Cross. Muiredach's cross is the most impressive surviving example of early medieval Irish stonework, and the crosses at Monasterboice have been said to be Ire...

UPS Airlines (UPS Air Cargo) IATA5X ICAOUPS Tên hiệuUPS Lịch sử hoạt độngThành lập1988; 36 năm trước (1988)Sân bay chínhTrạm trungchuyển chínhTrung tâm (Worldport) Louisville Mỹ Dallas Ontario (CA) Philadelphia Miami Chicago-Rockford Anchorage Canada Hamilton (ON) Châu Á Thượng Hải Hồng Kông[1] Singapore Thâm Quyến[2] Thông tin chung UPS Air CARGO 747-400F UPS Airlines (hay UPS Air Cargo) là hãng hàng không chở...