Mecanica contactului
|
Read other articles:

Baron Nils-Agustus Otto Carl Niclas Silfverschiöld (31 Mei 1934 – 11 April 2017) adalah seorang bangsawan dan tuan tanah Swedia. Dia menikah dengan Putri Désirée dari Swedia dan karena itu menjadi kakak ipar laki-laki Raja Carl XVI Gustaf dan ayah Baron Carl Silfverschiöld.[1] Baron Niclas SilfverschiöldBaron Niclas Silfverschiöld, 1964KelahiranBaron Niclas Silfverschiöld(1934-05-31)31 Mei 1934Kastil Coberg, SwediaKematian11 April 2017(2017-04-11) (umur 82)Paroki-Lagmans...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

BalşKotaNegara RumaniaProvinsiOltPemerintahan • Wali kotaVitalie StaicuLuas • Total37 km2 (14 sq mi)Populasi (2002) • Total21.195Zona waktuUTC+2 (EET) • Musim panas (DST)UTC+3 (EEST)Situs webhttp://www.bals.ro/ Balş adalah kota yang terletak di provinsi Olt, Rumania. Populasi 1864 - 1.700 1884 - 2.500 1921 - 5.000 1938 - 5.300 1948 - 6.128 1973 - 11.578 1992 - 24.560 2002 - 21.195 Komposisi penduduk menurut kebangsaan:...

Tujuh negara Arab yang berbatasan dengan Teluk Persia di pesisir baratnya dan Iran di pesisir timurnya. (semenanjung Musandam di Oman bertemu dengan teluk tersebut di Selat Hormuz.) Negara-negara Arab di Teluk Persia adalah tujuh negara Arab yang berbatasan dengan Teluk Persia, yakni Kuwait, Bahrain, Irak, Oman, Qatar, Arab Saudi dan Uni Emirat Arab (UEA).[1][2][3] Seluruh negara tersebut (dengan pengecualian Irak) adalah bagian dari Dewan Kerjasama Negara-Negara Teluk...
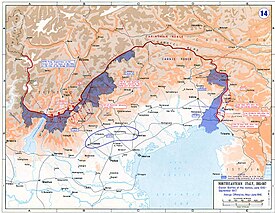
Pertempuran Isonzo ketigaBagian dari Blok Italia Perang Dunia ISebelas Pertempuran Isonzo Juni 1915 — September 1917Tanggal10 November—2 Desember 1915LokasiSungai Isonzo, Slovenia BaratHasil kemenangan ItaliaPihak terlibat Italia Austria-HungariaTokoh dan pemimpin Luigi Cadorna, Emanuele Filiberto, Duke Aosta II Svetozar Boroević, Archduke Eugen AustriaKekuatan 370 batalyon1.374 senjata 155 batalyon626 senjataKorban 49.500 (7.500 terbunuh) 32.100 (4.000 terbunuh) lbsBlok Italia Iso...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Partai Sosialis Serbia Социјалистичка Партија Србије Socijalistička Partija SrbijePresidenIvica DačićWakil presidenAleksandar AntićPresiden kehormatanMilutin MrkonjićPendiriSlobodan Milošević dan Milutin MrkonjićDibentuk17 Juli 1990; 33 tahun lalu (1990-07-17)Didahului olehLiga Komunis SerbiaKantor pusatStudentski trg 15 BelgradeKeanggotaan (2014)200,000[1]IdeologiPopulisme Sosialisme demokratikDemokrasi sosialNasionalisme sayap kiriPosisi&...

American actor (1901–59) John MertonMerton in Zorro's Fighting Legion, 1939BornMyrtland F. LaVarre(1901-02-18)February 18, 1901Seattle, Washington, United StatesDiedSeptember 19, 1959(1959-09-19) (aged 58)Los Angeles, California, United StatesOccupationActorYears active1927–1959SpouseEsther (divorced)Children6 John Merton (born Myrtland F. LaVarre; February 18, 1901 – September 19, 1959) was an American film actor.[1][2] He appeared in more than 250 films b...

Stelianos Malezas Informasi pribadiNama lengkap Stilianos MalezasTanggal lahir 11 Maret 1985 (umur 39)Tempat lahir Katerini, YunaniTinggi 1,93 m (6 ft 4 in)Posisi bermain Bek tengahInformasi klubKlub saat ini Fortuna DüsseldorfNomor 4Karier junior2000–2003 Pontioi KateriniKarier senior*Tahun Tim Tampil (Gol)2003–2012 PAOK 129 (3)2004–2005 → Irodotos (pinjam) 30 (1)2012– Fortuna Düsseldorf 7 (0)Tim nasional2010– Yunani 3 (0) * Penampilan dan gol di klub senio...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...

Questa voce sull'argomento doppiatori statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Mary Jessica Gibbs Mary Jessica Gibbs (Pasadena, 5 ottobre 1996) è una doppiatrice statunitense. Indice 1 Biografia 2 Filmografia 3 Altri progetti 4 Collegamenti esterni Biografia Mary Gibbs nasce nel 1996 a Pasadena, figlia unica del direttore e produttore cinematografico Rob Gibbs. Ha fatto il suo primo doppiaggio a 1 anno e mezzo in cui doppia Baby K...

Prime Minister of Poland (1915–2005) Edward SzczepanikSzczepanik in 1986.Prime Minister of PolandIn exile8 April 1986 – 22 December 1990PresidentKazimierz SabbatRyszard KaczorowskiPreceded byKazimierz SabbatSucceeded byTadeusz Mazowiecki(Third Polish Republic) Personal detailsBornEdward Franciszek Szczepanik22 August 1915Suwałki, Russian Empire(now Poland)Died11 October 2005(2005-10-11) (aged 90)Worcestershire, EnglandAlma materWarsaw School of Economics Edward Franciszek S...

Aubignascomune Aubignas – Veduta LocalizzazioneStato Francia RegioneAlvernia-Rodano-Alpi Dipartimento Ardèche ArrondissementPrivas CantoneLe Teil TerritorioCoordinate44°35′N 4°37′E / 44.583333°N 4.616667°E44.583333; 4.616667 (Aubignas)Coordinate: 44°35′N 4°37′E / 44.583333°N 4.616667°E44.583333; 4.616667 (Aubignas) Superficie15,4 km² Abitanti412[1] (2009) Densità26,75 ab./km² Altre informazioniCod. postale07400 F...

Maltese prelate of the Catholic Church His Excellency, The Most ReverendAntoine CamilleriApostolic Nuncio to CubaTitular Archbishop of SkálholtCamilleri in 2016ChurchCatholic ChurchAppointed20 May 2024PredecessorGiampiero GloderOther post(s)Titular Archbishop of SkálholtOrdersOrdination5 July 1991Consecration4 October 2019by Pope FrancisRankArchbishopPersonal detailsBorn (1965-08-20) 20 August 1965 (age 58)Sliema, MaltaNationalityMaltesePrevious post(s)Apostolic Nuncio to Ethiopia...

Japanese special police force The censorship section of the Special Higher Police bureau of the Tokyo Metropolitan PD. The Special Higher Police (特別高等警察, Tokubetsu Kōtō Keisatsu), often abbreviated Tokkō (特高, Tokkō), was, from 1911 to 1945, a Japanese policing organization, established within the Home Ministry for the purpose of carrying out high policing, domestic criminal investigations, and control of political groups and ideologies deemed to threaten the public order o...

Railway museum in Kyoto, Japan Kyoto Railway Museum京都鉄道博物館The museum entrance in October 2016Location of the museumShow map of Kyoto cityKyoto Railway Museum (Japan)Show map of JapanFormer nameUmekoji Steam Locomotive MuseumEstablished October 10, 1972 (1972-10-10) (as Umekoji Steam Locomotive Museum) April 29, 2016 (2016-04-29) (as Kyoto Railway Museum) LocationShimogyō-ku, Kyoto, JapanCoordinates34°59′14″N 135°44′33″E / ...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2020) قوة الرد السريع المشتركة الإنشاء 1999 جزء من القوات المسلحة البريطانية (خدمة ثلاثية) معدات البحرية الملكية قوات المارينز الملكية الجيش البريطاني القو...

721-й истребительный авиационный Касторненский орденов Суворова и Александра Невского полк Вооружённые силы ВС СССР Вид вооружённых сил ПВО ВВС Род войск (сил) истребительная авиация Почётные наименования «Касторненский» Формирование 12.10.1941 г. Расформирование (преобраз...

Pour les articles homonymes, voir Panhard (homonymie). Cet article possède un paronyme, voir Quai Panhard-et-Levassor. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article sur les transports doit être recyclé (août 2016). Une réorganisation et une clarification du contenu paraissent nécessaires. Améliorez-le, discutez des points à améliorer ou précisez les sections à recycler en utilisant {{section à recycler}}. Panhard Création 1889 Dates...

Railway station in Queensland, Australia NerangNorthbound view in April 2012General informationLocationLeagues Club Drive, NerangCoordinates27°59′39″S 153°21′00″E / 27.9941°S 153.3500°E / -27.9941; 153.3500Owned byQueensland RailOperated byQueensland RailLine(s)Gold CoastDistance75.89 kilometres from CentralPlatforms2 (1 island)Tracks2ConstructionStructure typeGroundBicycle facilitiesYesAccessibleYesOther informationStatusStaffedStation code600185 (platform...













































