Mașină Turing nedeterministă
|
Read other articles:

2007 soundtrack album by Vishal–Shekhar, PyarelalOm Shanti OmSoundtrack album by Vishal–Shekhar, PyarelalReleased9 September 2007GenreFeature film soundtrackLength61:18LabelT-SeriesProducerGauri Khan Om Shanti Om is the soundtrack to the 2007 film of the same name directed by Farah Khan, produced by Gauri Khan through Red Chillies Entertainment and starred Shah Rukh Khan, Arjun Rampal and Deepika Padukone (in her film debut). The film's soundtrack featured six original songs, four...

Katedral TelšiaiKatedral Santo Antonius dari PaduaLithuanian: Šv. Antano Paduviečio katedracode: lt is deprecated Katedral TelšiaiKatedral Telšiai55°58′56″N 22°14′47″E / 55.98222°N 22.24639°E / 55.98222; 22.24639Koordinat: 55°58′56″N 22°14′47″E / 55.98222°N 22.24639°E / 55.98222; 22.24639LokasiTelšiaiNegara LituaniaDenominasiGereja Katolik RomaSejarahTanggal konsekrasi1794ArsitekturStatusKatedralStatus fungsion...

Tulisan Eben-Haëzer di Gereja Turfmarkt, Gouda, Belanda Tulisan: Eben-Ezer pada Matthaus Frank House [he], sekarang #6 Emek Refaim Street di Yerusalem Eben-Haezer (Ibrani: אבן העזרcode: he is deprecated , Even Ha'Ezer, artinya batu pertolongan; Inggris: Eben-Ezercode: en is deprecated atau Ebenezer) adalah nama tempat kuno di Israel yang dicatat dalam Alkitab Ibrani dan Perjanjian Lama dalam Alkitab Kristen, khususnya dalam Kitab 1 Samuel. Merupakan tempat beberapa pertem...

العلاقات العمانية المنغولية سلطنة عمان منغوليا سلطنة عمان منغوليا تعديل مصدري - تعديل العلاقات العمانية المنغولية هي العلاقات الثنائية التي تجمع بين سلطنة عمان ومنغوليا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: ...
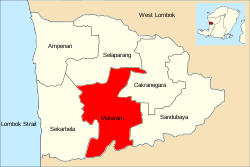
MataramKecamatanPeta lokasi Kecamatan MataramNegara IndonesiaProvinsiNusa Tenggara BaratKotaMataramKode Kemendagri52.71.02 Kode BPS5271020 Desa/kelurahan9 Kelurahan Mataram adalah sebuah kecamatan di kota Mataram, Nusa Tenggara Barat, Indonesia.[1][2] Pemerintahan Pembagian administratif Kecamatan Mataram dibagi dalam 9 Kelurahan, yaitu: Mataram Timur Pagesangan Pagesangan Barat Pagesangan Timur Pagutan Pagutan Barat Pagutan Timur Pejanggik Punia Referensi ^ Kecamatan Mat...

Remembrance day Part of a series onJewish exodus from the Muslim world Background History of the Jews under Muslim rule Sephardi Mizrahi Yemeni Zionism Arab–Israeli conflict 1948 war Suez Crisis Six-Day War Antisemitism in the Arab world Farhud Aleppo Aden Oujda and Jerada Tripolitania Cairo Baghdad Tripoli Exodus by country Morocco Operation Mural Operation Yachin Egoz Yemen Iraq Egypt Lebanon Iran Tunisia Hurum air disaster Remembrance Awareness day JIMENA JJAC WOJAC The Forgotten Refugee...

ロバート・デ・ニーロRobert De Niro 2011年のデ・ニーロ生年月日 (1943-08-17) 1943年8月17日(80歳)出生地 アメリカ合衆国・ニューヨーク州ニューヨーク市身長 177 cm職業 俳優、映画監督、映画プロデューサージャンル 映画、テレビドラマ活動期間 1963年 -配偶者 ダイアン・アボット(1976年 - 1988年)グレイス・ハイタワー(1997年 - )主な作品 『ミーン・ストリート』(1973年)...

Body of criticism of the European Union This article is about opposition to or scepticism on the European Union. For dislike of European culture and European ethnic groups by non-Europeans, see Anti-Europeanism. Public opinion on the European Union in 2022 This article is part of a series onPolitics of the European Union Member states (27) Austria Belgium Bulgaria Croatia Cyprus Czech Republic Denmark Estonia Finland France Germany G...

Questa voce sull'argomento fiction televisive tedesche è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. LindenstraßeIl logo della fiction utilizzato dal 1985 al 2015Titolo originaleLindenstraße PaeseGermania Anno1985-2020 Formatoserial TV Generesoap opera Stagioni1 Puntate1.758[1][2][3][4] Durata29 min. (ep.) Lingua originaleTedesco CreditiIdeatoreHans W. Geißendörfer RegiaHerwig FischerDominikus Probst George Moorse...

Ираклеониты — ученики гностика Ираклеона (II век). Упоминаются как особая секта Епифанием и Августином; при крещении и миропомазании они соблюдали обряд помазания елеем и при этом произносили воззвания на арамейском языке, которые должны были освободить душу от власт�...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Canadian ice hockey player Ice hockey player Trevor Gillies Gillies warming up with the New York Islanders in 2011.Born (1979-01-30) January 30, 1979 (age 45)Cambridge, Ontario, CanadaHeight 6 ft 3 in (191 cm)Weight 227 lb (103 kg; 16 st 3 lb)Position Left wingShot LeftPlayed for Mighty Ducks of AnaheimNew York IslandersVityaz ChekhovHIFKNHL draft UndraftedPlaying career 1999–2018 Trevor Gillies (born January 30, 1979) is a Canadian former profess...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

الحملة البريطانية على التبت التاريخ وسيط property غير متوفر. بداية ديسمبر 1903 نهاية سبتمبر 1904 البلد الصين الموقع التبت 26°05′20″N 89°16′37″E / 26.08888889°N 89.27694444°E / 26.08888889; 89.27694444 تعديل مصدري - تعديل بدأت الحملة البريطانية على التبت (تُدعى أيضًا الغز�...

This is a list of foreign ministers in 2017.[1] Africa Algeria Ramtane Lamamra (2013–2017) Abdelkader Messahel (2017–2019) Angola - Georges Rebelo Chicoti (2010–2017) Manuel Domingos Augusto (2017–2020) Benin - Aurélien Agbénonci (2016–2023) Botswana - Pelonomi Venson-Moitoi (2014–2018) Burkina Faso - Alpha Barry (2016–2021) Burundi - Alain Aimé Nyamitwe (2015–2018) Cameroon- Lejeune Mbella Mbella (2015–present) Cap...

Chinese retail company Suning Appliance redirects here. For other companies, see Suning. Not to be confused with Suning Appliance Group. Suning.com Co., Ltd.FormerlySuning Domestic ApplianceSuning Domestic Appliance (Group)Suning Appliance Chain Store (Group)Suning ApplianceSuning Commerce GroupCompany typePublicTraded asSZSE: 002024IndustryRetailFounded1990 (predecessor)15 May 1996 (1996-05-15) (date of incorporation of Suning Domestic Applia...

American chemist For other people named John D. Roberts, see J. D. Roberts (disambiguation) John D. RobertsJohn D. Roberts in 2010BornJohn Dombrowski Roberts(1918-06-08)June 8, 1918Los Angeles, California, U.S.DiedOctober 29, 2016(2016-10-29) (aged 98)Pasadena, California, U.S.NationalityAmericanAlma materUCLAAwards ACS Award in Pure Chemistry (1954) Roger Adams Award in Organic Chemistry (1967) William H. Nichols Medal (1972) Tolman Award (1974) Willard Gibbs Award (1983) Priestley...

Sayida Ounissi Sayida Ounissi en 2014. Fonctions Députée de la première circonscription de la France 13 novembre 2019 – 13 décembre 2021(2 ans et 1 mois) Élection 6 octobre 2019 Législature IIe Groupe politique Ennahdha 2 décembre 2014 – 16 septembre 2016(1 an, 9 mois et 14 jours) Élection 26 octobre 2014 Législature Ire Groupe politique Ennahdha Successeur Karima Taggaz[1],[2] Ministre tunisienne de l'Emploi et de la Formation professionnelle 14 novembr...

Dutch architect Abe BonnemaHome of Bonnema in Hurdegaryp in 2014BornAbe Bonnema(1926-09-06)6 September 1926Stiens, NetherlandsDied9 August 2001(2001-08-09) (aged 74)GroningenNationalityDutchAlma materTU DelftOccupationArchitectPracticeBonnema ArchitectenBuildingsGebouw Delftse Poort in Rotterdam Achmeatoren in Leeuwarden Het Boek, Amsterdam Abe Bonnema (6 September 1926 – 9 August 2001) was a Dutch architect.[1] He studied architectural engineering at the Delft University ...














