Hiperon
|
Read other articles:

Bafétimbi Gomis Gomis bermain untuk Swansea City pada 2015Informasi pribadiNama lengkap Bafétimbi Gomis[1]Tanggal lahir 6 Agustus 1985 (umur 38)[2]Tempat lahir La Seyne-sur-Mer, PrancisTinggi 1,86 m (6 ft 1 in)[3]Posisi bermain PenyerangInformasi klubKlub saat ini Kawasaki FrontaleNomor 18Karier junior1994–2000 Toulon Var2000–2004 Saint-ÉtienneKarier senior*Tahun Tim Tampil (Gol)2004–2009 Saint-Étienne 142 (40)2005 → Troyes (pinjaman) 1...

Artikel ini mungkin terdampak dengan peristiwa terkini: Tragedi Stadion Kanjuruhan 2022. Informasi di halaman ini bisa berubah setiap saat. Stadion Kanjuruhan Informasi stadionPemilikPemerintah Kabupaten MalangLokasiLokasi Kepanjen, Kabupaten Malang, Jawa Timur, IndonesiaKoordinat8°9′2″LS,112°34′23″BTKonstruksiMulai pembangunan1997Dibuka9 Juni 2004 (2004-06-09)Direnovasi2010Ditutup3 Oktober 2022 (2022-10-03)Biaya pembuatanRp 35 miliarData teknisPermukaanRumput LokalPapan s...

Aksara LaoJenis aksara Abugida BahasaLaoThaidan lain-lainPeriodec. 1350–kiniArah penulisanKiri ke kananAksara terkaitSilsilahMenurut hipotesis hubungan antara abjad Aramea dengan Brahmi, maka silsilahnya sebagai berikut: Abjad Proto-Sinai Abjad Fenisia Abjad Aramea Aksara Brahmi Dari aksara Brahmi diturunkanlah:Aksara PallawaAksara KhmerAksara ThaiAksara LaoISO 15924ISO 15924Laoo, 356 , LaoPengkodean UnicodeNama UnicodeLaoRentang UnicodeU+0E80–U+0EFF Artikel ini men...

2016 film by Mandie Fletcher Absolutely Fabulous: The MovieTheatrical release posterDirected byMandie FletcherWritten byJennifer SaundersBased onAbsolutely Fabulousby Jennifer Saunders and Dawn FrenchProduced by Damian Jones Jon Plowman Starring Jennifer Saunders Joanna Lumley Julia Sawalha Jane Horrocks June Whitfield Chris Colfer Kate Moss Lulu Emma Bunton Robert Webb Barry Humphries CinematographyChris GoodgerEdited by Anthony Boys Gavin Buckley Music byJake MonacoProductioncompanies Fox S...

Confederate general during the American Civil War Archibald C. GodwinBorn1831Nansemond County, VirginiaDiedSeptember 19, 1864 (aged 32–33)Winchester, VirginiaPlace of burialStonewall Cemetery in Winchester, VirginiaAllegiance Confederate States of AmericaService/branch Confederate States ArmyYears of service1861-1864RankColonel Brigadier General (unconfirmed)Battles/warsAmerican Civil War Battle of Fredericksburg Battle of Chancellorsville Battle of Gettysburg Battle...

For the former shopping mall in New Jersey, see Burlington Center Mall. Shopping mallBurlington CentreThe Burlington Centre entrance in 2007Coordinates43°20′51″N 79°47′42″W / 43.3475°N 79.7949°W / 43.3475; -79.7949Address777 Guelph LineBurlington, Ontario, CanadaL7R 3N2Opening date1968OwnerPrimaris ReitNo. of stores and services132No. of anchor tenants8No. of floors2Parking4,623Websiteburlingtoncentre.ca Burlington Centre (formerly known as Burlington Mall)...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Voce principale: Associazione Sportiva Bari. Associazione Sportiva BariStagione 1972-1973Il Bari del 1972-1973, nel ritiro estivo (pre campionato) di Pavullo nel Frignano. Le persone fotografate sono (a partire da sinistra): (in alto) l'allenatore Regalia, Sigarini, Casarsa, Galli, Spimi, il commendator Albanese, Colombo, P. Loseto, Cazzola, Marcolini, Martini, Ardemagni; (in ginocchio) il massaggiatore Chiesa, Tessarotto, Lopez, Butti, Consonni, Dalle Vedove, Generoso, il segretario Nitti e...
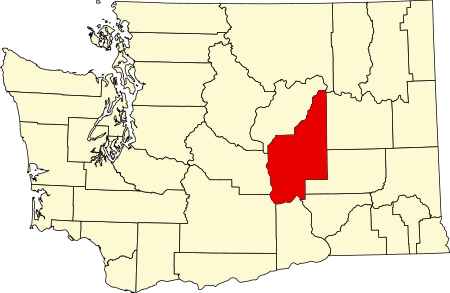
Эта статья об округе в штате Вашингтон; другие значения: Грант (округ). ОкругГрантангл. Grant County 47°13′ с. ш. 119°28′ з. д.HGЯO Страна США Входит в штат Вашингтон Адм. центр Эфрейта[англ.] История и география Дата образования 24 февраля 1909 Площадь 7229 км² (6944 км² — с�...

Pour les articles homonymes, voir Frisch. Edmond de FelsEdmond de FelsFonctionPrésidentSociété des amis de Versailles1943-1951Alexandre MillerandPierre de Cossé-BrissacTitre de noblesseComte romainBiographieNaissance 3 juillet 1858MarseilleDécès 29 mars 1951 (à 92 ans)8e arrondissement de ParisNationalité françaiseActivité DiplomateEnfants André de FelsHubert Frisch de Fels (d)Anne Marie Frisch de Fels (d)Edmée de La RochefoucauldAutres informationsPropriétaire de Châ...

ديميتار لارغوف (بالبلغارية: Димитър Ларгов) معلومات شخصية الميلاد 10 سبتمبر 1936(1936-09-10)صوفيا الوفاة 26 نوفمبر 2020 (عن عمر ناهز 84 عاماً)صوفيا مركز اللعب وسط الجنسية بلغاريا مسيرة الشباب سنوات فريق 1946–1953 Cherveno Zname Sofia المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1954–1955 سب...

Canadian politician Jennifer RiceMLAParliamentary Secretary for Emergency Preparedness of British ColumbiaIn officeJuly 18, 2017 – January 20, 2023Preceded byNaomi Yamamoto (As Minister of Emergency Preparedness)Member of the British Columbia Legislative Assemblyfor North CoastIncumbentAssumed office May 14, 2013Preceded byGary CoonsPrince Rupert City CouncillorIn officeNovember 19, 2011 – June 10, 2013 Personal detailsBornOttawa, Ontario, CanadaPolitical partyNew De...

Feudal practice English feudalismHarold Sacramentum Fecit Willelmo Duci(Bayeux Tapestry) FiefEcclesiastical fiefCrown landAllodial titleAppanageVassalFeoffmentSeignorySubinfeudationFeoffeeFealtyHomageAffinityFeudal maintenanceFeudal fragmentationBastard feudalismLivery Manorialism Lord of the manorManorial courtManor house (List)DemesneGlebeOverlordLordPeasantSerfdomFree tenant Feudal land tenure in England Land tenureEnglish feudal baronyFeudal baronKnight's feeKnight-serviceBaronagePeerageS...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dodge Monaco – news · newspapers · books · scholar · JSTOR (August 2014) (Learn how and when to remove this...

Brandon LeeNama Tionghoa李國豪 (Tradisional)Nama Tionghoa李国豪 (Sederhana)PinyinLǐ Guóháo (Mandarin)JyutpingLei Gwok Hou (Kanton)Nama LahirBrandon Bruce LeeLeluhurShunde, Guangdong, ChinaLahir(1965-02-01)1 Februari 1965Oakland, California, Amerika SerikatWafat31 Maret 1993(1993-03-31) (umur 28)Carolina Utara, Amerika SerikatTahun aktif1986–1993Orang tuaBruce Lee (1940–1973)Linda Lee Cadwell (1945–)PartnerEliza Hutton (1990–1993) Brandon Bruce Lee (Hanzi: 李國豪, Piny...

Type of mechanical seal This article is about mechanical seals. For other uses, see Gasket (disambiguation). Some seals and gaskets 1. o-ring2. fiber washer3. paper gasket4. cylinder head gasket A gasket is a mechanical seal which fills the space between two or more mating surfaces, generally to prevent leakage from or into the joined objects while under compression. It is a deformable material that is used to create a static seal and maintain that seal under various operating conditions in a...

Crude oil discovery in Alberta, Canada in Alberta, CanadaLeduc No. 1Leduc #1 wellTypecrude oil discovery in Alberta, CanadaLocationAlberta, CanadaNearest cityLeduc CountyEstablished1990Built1946Governing bodyParks CanadaWebsitehttp://www.canadianenergymuseum.ca/ National Historic Site of Canada Leduc No. 1 was a major crude oil discovery made near Leduc, Alberta, Canada, on February 13, 1947. It provided the geological key to Alberta's most prolific conventional oil reserves and resulted in ...

Cet article est une ébauche concernant un objet mineur du Système solaire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Animation montrant l'orbite de six troyens au point de Lagrange L4, dans un référentiel en rotation avec une période égale à celle de Neptune, Neptune est donc stationnaire et représentée par le point blanc à 315°. Un astéroïde troyen de Neptune est un astéroïde dont l'orbite ...

1999 single by Bryan Adams For other uses, see Cloud Nine (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cloud Number Nine – news · newspapers · books · scholar · JSTOR (January 2019) (Learn how and when to remove this message) Cloud Number NineSingle by Bryan Adamsfrom the album On a Day ...

Monetary exemption from taxes that would otherwise be levied Part of a series onTaxation An aspect of fiscal policy Policies Government revenue Property tax equalization Tax revenue Non-tax revenue Tax law Tax bracket Flat tax Tax threshold Exemption Credit Deduction Tax shift Tax cut Tax holiday Tax amnesty Tax advantage Tax incentive Tax reform Tax harmonization Tax competition Tax withholding Double taxation Representation Unions Medical savings account Economics General Theory Price effec...
