Índice Dunn
|
Read other articles:

City in Utah, United States For other uses, see Manti (disambiguation). City in Utah, United StatesManti, UtahCityBirdseye view of Manti and the Sanpete Valley, August 2004Location in Sanpete County and the state of Utah.Coordinates: 39°15′53″N 111°38′20″W / 39.26472°N 111.63889°W / 39.26472; -111.63889CountryUnited StatesStateUtahCountySanpeteFounded1849Incorporated1851Founded byGeorge Washington Bradley and Isaac MorleyNamed forA city in the Book of Mormo...

Explore Scientific LLCCompany typeLLCIndustryImaging/ManufacturingFoundedLaguna Hills, California (2008)HeadquartersSpringdale, ArkansasProductsTelescopes, spotting scopes, binoculars, eyepieces and microscopesOwnerJourneyNorth Inc. (2014–present)Websitewww.explorescientificusa.com Explore Scientific is a company founded by former Meade Instruments Vice President of Brand Community Scott W. Roberts in 2008. Headquartered in Springdale, Arkansas, the company designs and manufactures telescop...

American architect (1867–1959) This article's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (February 2024) (Learn how and when to remove this message) Frank Lloyd WrightWright in 1954Born(1867-06-08)June 8, 1867Richland Center, Wisconsin, U.S.DiedApril 9, 1959(1959-04-09) (aged 91)Phoenix, Arizona, U.S.Alm...

The British folk revival incorporates a number of movements for the collection, preservation and performance of folk music in the United Kingdom and related territories and countries, which had origins as early as the 18th century. It is particularly associated with two movements, usually referred to as the first and second revivals, respectively in the late 19th to early 20th centuries and the mid-20th century. The first included increased interest in and study of traditional folk music, th...

Species of shark Blacktailed spurdog from New Caledonia Conservation status Data Deficient (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Chondrichthyes Subclass: Elasmobranchii Subdivision: Selachimorpha Order: Squaliformes Family: Squalidae Genus: Squalus Species: S. melanurus Binomial name Squalus melanurusFourmanoir & Rivaton, 1979 Range of the blacktailed spurdog (in blue) Sharks portal The blacktailed spurdog (S...

Month of 1966 1966 January February March April May June July August September October November December << July 1966 >> Su Mo Tu We Th Fr Sa 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 July 18, 1966: Young and Collins go further from Earth than anyone before July 30, 1966: England wins the World Cup at Wembley July 18, 1966: Sukarno, the Father of Indonesia, loses most of his power The following events occurred in July 1966:...

Dubel Meriyenes Informasi pribadiLahir15 Agustus 1957 (umur 66) Padang, Sumatera BaratAlma materSepawamil (1986)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan DaratMasa dinas1986–2015Pangkat Brigadir Jenderal TNISatuanCorps Kesehatan Militer (Ckm)Sunting kotak info • L • B Letnan Jenderal TNI (Purn.) dr. Dubel Meriyenes, Sp.B., FINACS (lahir 15 Agustus 1957) adalah seorang Purnawirawan perwira tinggi TNI Angkatan Darat yang pernah menjabat sebagai Direkt...

Cubiérettes Blason Administration Pays France Région Occitanie Département Lozère Arrondissement Mende Intercommunalité Communauté de communes Mont Lozère Maire Mandat Christian Benoit 2020-2026 Code postal 48190 Code commune 48054 Démographie Gentilé Cubiérettois Populationmunicipale 47 hab. (2021 ) Densité 4,1 hab./km2 Géographie Coordonnées 44° 27′ 36″ nord, 3° 47′ 16″ est Altitude Min. 960 mMax. 1 625 m Superfi...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Spanish baseball coach (born 1983) Baseball player Paco FigueroaFigueroa with the Phillies in 2022Philadelphia Phillies – No. 38Second baseman / CoachBorn: Francisco Figueroa (1983-02-19) 19 February 1983 (age 41)Miami, Florida, U.S.Bats: RightThrows: Right TeamsAs coach Philadelphia Phillies (2019–present) Francisco Paco Figueroa (born 19 February 1983) is a baseball coach and former professional player who played as a second baseman. Born in the United States, he represented Spain ...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Konstantinos X DoukasKaisar dan Otokrat RomawiHistamenon emas Konstantinos X.Kaisar Kekaisaran BizantiumBerkuasa24 November 1059 – 22 Mei 1067PendahuluIsaac I KomnenosPenerusRomanos IV DiogenesInformasi pribadiKelahiran1006Kematian22 Mei 1067 (usia 61)AyahAndronikos DoukasPasangantidak diketahuiEudokia MakrembolitissaAnakMichael VII DoukasAndronikos DoukasKonstantios DoukasAnna DoukainaTheodora Anna DoukainaZoe Doukaina Konstantinos X Doukas atau Dukas, di-Latinisasi menjadi ...

Tujuan Dana Inovasi Uni Eropa Dana Inovasi Uni Eropa (Bahasa Inggris: EU's Innovation Fund) adalah sebuah program pendanaan penanggulan perubahan iklim terbesar di dunia. Negara-negara di Uni Eropa bekerjasama untuk mengatasi perubahan iklim global.[1] Dana Inovasi ini merupakan pendanaan yang disiapkan Sistem Perdagangan Emisi UE (EU Emissions Trading System disingkat EU ETS) yang telah direvisi.[2] Uni Eropa bergerak cepat untuk mengatasi pemanasan global, perubahan iklim, g...

Northern Europe Ireland Uilleann pipes: Also known as Union pipes and Irish pipes, depending on era. Bellows-blown bagpipe with keyed or un-keyed 2-octave chanter, 3 drones and 3 regulators. The most common type of bagpipes in Irish traditional music. Great Irish Warpipes: One of the earliest references to the Irish bagpipes comes from an account of the funeral of Donnchadh mac Ceallach, king of Osraige in AD 927.[1] Bagpipes were a noted instrument in Irish warfare since medieval ti...

English computer scientist (1912–1954) Turing redirects here. For other uses, see Turing (disambiguation). Alan TuringOBE FRSTuring in 1936BornAlan Mathison Turing(1912-06-23)23 June 1912Maida Vale, London, EnglandDied7 June 1954(1954-06-07) (aged 41)Wilmslow, Cheshire, EnglandCause of deathCyanide poisoning as an act of suicide[note 1]Alma mater University of Cambridge (BA, MA) Princeton University (PhD) Known for Cryptanalysis of the Enigma Turing's proof T...

Tamil Emigration: Early migrations (before 1800s) - Various destinations, Medieval period A map of the territories and five states in South India. The South Indian diaspora (Tamil: அயலகத் தென்னிந்தியர்) (Malayalam: തെന്നിന്ത്യൻ പ്രവാസികൾ) (Kannada: ದಕ್ಷಿಣ ಭಾರತೀಯ ವಲಸೆಗಾರ) (Telugu: దక్షిణ భారత డయాస్పోరా) comprises people who have emigrated f...

The Great Hallof the University of SydneyThe interior of the Great HallGeneral informationStatusCompletedArchitectural styleVictorian Academic Gothic revivalLocationMain Quadrangle, The University of Sydney, Camperdown Campus, Sydney, New South WalesCountryAustraliaCoordinates33°53′07″S 151°11′20″E / 33.8854°S 151.1890°E / -33.8854; 151.1890Construction started1855CompletedJuly 1859 (1859-07)OwnerThe University of SydneyTechnical detailsMaterialS...

Higher education school in Malaysia Fire and Rescue Academy of MalaysiaAkademi Bomba dan Penyelamat MalaysiaFormer namesSekolah Latihan Bomba Malayan Union (1957)Pusat Latihan Bomba (1958–1997)TypePublicEstablished1957 (1957)Affiliation Fire and Rescue Department of MalaysiaOfficer in chargeSenior Assistant Fire Commissioner Md Ali Ismail, Assistant Director General of the TrainingLocation MalaysiaCampusMultiple sites, 470.6 acres (190.4 ha) (For 5 campuses)Websitefram.bomba....
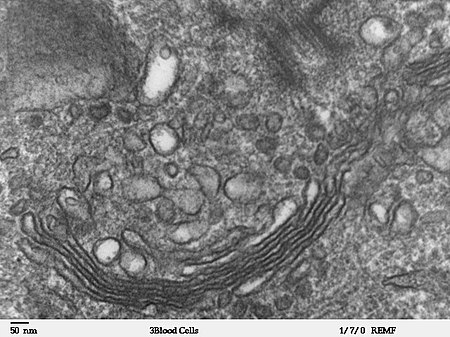
Biologi selSel hewanKomponen sel hewan pada umumnya: Nukleolus Inti sel Ribosom (titik-titik kecil sebagai bagian dari no. 5) Vesikel Retikulum endoplasma kasar Badan Golgi Sitoskeleton Retikulum endoplasma halus Mitokondria Vakuola Sitosol (cairan yang berisi organel, yang terdiri dari sitoplasma) Lisosom Sentrosom Membran sel Mikrograf badan Golgi, terlihat sebagai tumpukan cincin setengah lingkaran berwarna hitam di bagian bawah gambar. Sejumlah vesikel bulat terlihat di sekitar organel in...

Unincorporated community in Virginia, United States This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Damon, Virginia – news · newspapers · books · scholar · JSTOR (January 2024)Unincorporated community in Virginia, United StatesDamonUnincorporated communityDamonLocation within the state of VirginiaS...



















