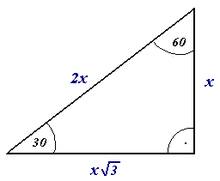
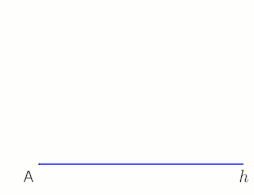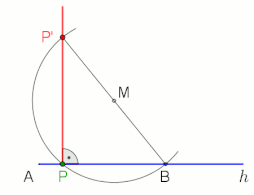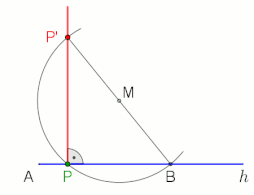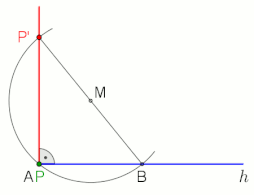
Ângulo reto
|
Read other articles:

Peta lokasi Botolan Botolan adalah munisipalitas yang terletak di provinsi Zambales, Filipina. Menurut sensus tahun 2020, wilayah ini memiliki jumlah penduduk sebesar 66.739 jiwa dan 13.627 rumah tangga. Barangay Botolan terbagi menjadi 31 barangay. Bancal Bangan Batonlapoc Belbel Beneg Binuclutan Burgos Cabatuan Capayawan Carael Danacbunga Maguisguis Malomboy Mambog Moraza Nacolcol Owaog-Nibloc Paco (Pob.) Palis Panan Parel Paudpod Poonbato Porac San Isidro San Juan San Miguel Santiago Tampo...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Dlingo, Mojosongo, Boyolali – berita · surat kabar · buku · cendekiawan · JSTOR DlingoDesaKantor Desa DlingoNegara IndonesiaProvinsiJawa TengahKabupatenBoyolaliKecamatanMojosongoKode pos57322Kode Ke...

Gereja Kristen SumbaLogo GKSPenggolonganProtestan, CalvinisPemimpin(Ketua Umum) Pdt.Marlin Lomi S.ThWilayahNTTDidirikan15 Januari 1947 Sumba, NTTUmat386.000 jiwa Gereja Kristen Sumba (disingkat GKS) ialah suatu organisasi gereja Kristen Protestan di Indonesia, wadah penginjilan dan wadah penyatuan umat Protestan aliran Calvin yang memiliki wilayah di pulau Sumba. Saat ini, gereja-gereja dari Sinode GKS sudah/telah hadir di beberapa kota lain di luar Pulau Sumba. Sejarah Hari lahir GKS bertepa...

هذه المقالة عن نطاق إنترنت خاص بدولة، لمزيد من المواضيع المتعلقة يمكنك زيارة مقالة CV .cv البلد الرأس الأخضر الموقع الموقع الرسمي تعديل مصدري - تعديل cv. هو امتداد خاص بالعناوين الإلكترونية (نطاق) domain للمواقع التي تنتمي إلى كابى فيردى (بالمحيط الأطلنطي).[1][2] و...

Stadion Artemio FranchiStadion Comunale Informasi stadionNama lamaStadion ComunalePemilikPemerintah Kota FirenzeLokasiLokasiViale Manfredo Fanti 4a, 50137 Firenze, ItaliaKoordinat43°46′50.96″N 11°16′56.13″E / 43.7808222°N 11.2822583°E / 43.7808222; 11.2822583Koordinat: 43°46′50.96″N 11°16′56.13″E / 43.7808222°N 11.2822583°E / 43.7808222; 11.2822583KonstruksiDibuka1931Direnovasi1990 & 2003[1][2]ArsitekP...

Cook Up a StormSutradaraRaymond YipProduserMani FokManfred WongSkenarioManfred WongLiu YiHana LiPemeranNicholas TseJung Yong-hwaGe YouTiffany TangMichelle BaiAnthony WongPenata musikAlex SanChan Kwong-wingSinematograferYip Shiu-keiPenyuntingShirley YipYu HongchaoPerusahaanproduksiEmperor Motion PicturesWanda PicturesDistributorEmperor Motion PicturesTanggal rilis 10 Februari 2017 (2017-02-10) NegaraHong KongTiongkokBahasaKantonMandarinAnggaranCN¥ 250 jutaPendapatankotorCN¥&#...

Period of the Byzantine Empire that created a new army that served from 1081 AD – 1204 AD Byzantine army of the Komnenian periodEmperor John II Komnenos, the most successful commander of the Komnenian army.LeadersByzantine EmperorDates of operation1081–1204 ADHeadquartersConstantinopleActive regionsAnatolia, Southern Italy, Balkans, Hungary, Galicia, Crimea, Syria, Egypt.Size50,000[1] (1143-1180)Part ofByzantine EmpireAlliesVenice, Genoa, Danishmends, Georgia, Galicia, Vladim...

Questa voce sull'argomento politici statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Ralph Bunche Premio Nobel per la pace 1950 Raphael Johnson Bunche (Detroit, 7 agosto 1903 – New York, 9 dicembre 1971) è stato un politologo e diplomatico statunitense. Indice 1 Biografia 2 Onorificenze 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Biografia Fu Premio Nobel per la pace nel 1...

Sebastiano FolliNaissance 1568SienneDécès 1621SienneActivité PeintreLieux de travail Rome (1605), Sienne (1606-1621), Siennemodifier - modifier le code - modifier Wikidata Vierge à l'Enfant, fresque, église San Biagio, Castiglione d'Orcia. Sebastiano Folli (Sienne, 1568-1621) est un peintre italien qui fut actif principalement dans sa ville natale, dans le sud de la Toscane et à Rome. Biographie Sebastiano Folli, élève d'Alessandro Casolano, est surtout connu pour les diverses fresque...

Teatro dell'Oceano Indianoparte della seconda guerra mondialePortaerei inglese HMS Hermes (95) affondata durante l'incursione giapponese nell'Oceano IndianoData1940 - 15 agosto 1945 LuogoOceano Indiano EsitoVittoria alleata SchieramentiAlleati Impero britannico India Britannica Sceiccato del Kuwait Kedah Stati della Tregua Abu Dhabi Qatar Nuova Zelanda Australia Stati Uniti Francia libera Paesi BassiPotenze dell'Asse Germania Impero giapponese Regno d'Itali...

ГородТегусигальпаисп. Tegucigalpa Флаг 14°05′39″ с. ш. 87°12′24″ з. д.HGЯO Страна Гондурас[1] департамент Франсиско Морасан Мэр Насри Асфура История и география Основан 1578 Первое упоминание 1578 Город с 1578 Площадь 201,5 км² Высота центра 990 м Часовой пояс UTC−6:00 Н�...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

American business magnate and philanthropist (1839–1937) For other people named John D. Rockefeller, see John D. Rockefeller (disambiguation). John D. RockefellerRockefeller in 1895BornJohn Davison Rockefeller(1839-07-08)July 8, 1839Richford, New York, U.S.DiedMay 23, 1937(1937-05-23) (aged 97)Ormond Beach, Florida, U.S.Burial placeLake View Cemetery in Cleveland 41°30′40″N 81°35′28″W / 41.511°N 81.591°W / 41.511; -81.591OccupationsBusinessmanphilant...

Scottish musical duo Saint PhnxBackground informationOriginWishaw, ScotlandGenres Alternative pop[1][2] indie pop[3] Years active2016–presentLabelsAtlantic, DDMNMembers Alan Jukes Stevie Jukes Websitesaintphnx.com Saint Phnx (pronounced saint phoenix and stylized as SAINT PHNX) are a Scottish musical duo formed by brothers Alan and Stevie Jukes in 2016. Currently signed to Atlantic Records, they released their debut studio album DDMN on 31 January 2020. On 2 July 202...

1806 revolt against the East India Company Vellore Sepoy MutinyPillar at Hazrath Makkaan Junction commemorating the Vellore sepoy mutiny.Date10 July 1806 (1806-07-10)Duration1 dayLocationVellore FortVellore, Madras Presidency, Company RajTypeMutinyCasualtiesIndian rebel sepoys: 100 summarily executed. Total 350 sepoys killed, 350 wounded.British officers of sepoy regiments: 14British soldiers of 69th Regiment: 115 The Vellore mutiny, or Vellore Revolution, occurred on 10 July 1...

BOP1 معرفات أسماء بديلة BOP1, block of proliferation 1, ribosomal biogenesis factor معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 610596 MGI: MGI:1334460 HomoloGene: 6612 GeneCards: 23246 علم الوجود الجيني وظائف جزيئية • ribonucleoprotein complex binding• GO:0001948، GO:0016582 ربط بروتيني• RNA binding مكونات خلوية • نوية• نواة• PeBoW complex• بلا�...

Indian politician and activist (born 1956) Maneka GandhiGandhi in 2014Minister of Women and Child Development, Government Of IndiaIn office26 May 2014 (2014-05-26) – 24 May 2019 (2019-05-24)Prime MinisterNarendra ModiPreceded byKrishna TirathSucceeded bySmriti IraniMember of Parliament, Lok SabhaIn office23 May 2019 (2019-05-23) – 4 June 2024Preceded byVarun GandhiSucceeded byRambhual NishadConstituencySultanpurIn office2014&#...

Maison de Sonderbourg Armoiries de la maison de Sonderbourg. Données clés Pays Allemagne Danemark Lignée Maison d'Oldenbourg Titres Duc de SonderbourgDuc de Franzhagen Fondation 1564Jean de Schleswig-Holstein (1545-1622) Déposition Alexandre-Rodolphe de Schleswig-Holstein-Sonderbourg (1651-1737) Dissolution 1737 Ethnicité Allemande Branche Maison d'AugustenbourgMaison de GlücksbourgMaison de Plön modifier La maison de Sonderbourg, ou dans sa forme longue la maison de Schleswig-Holstei...

В Википедии есть статьи о других людях с такой фамилией, см. Романов; Романов, Александр. Эта страница требует существенной переработки. Возможно, её необходимо правильно оформить, дополнить или переписать.Пояснение причин и обсуждение — на странице Википедия:К улучшени...

Устойчивый трифенилметильный радикал Свободные радикалы в химии — частицы, содержащие один или несколько неспаренных электронов на внешней электронной оболочке. Свободные радикалы бывают твёрдыми, жидкими и газообразными веществами и могут существовать от очень к...