Trítono

Chamamos de Trítono um intervalo entre alturas de duas notas musicais que possua exatamente três tons inteiros. O efeito denominado trítono consiste numa dissonância.

Caracteriza-se por um intervalo de 4ª aumentada (#4) ou 5ª diminuta (b5) entre as notas. Pode-se afirmar que a maneira mais comum de se aplicar o trítono consiste em inseri-lo nos acordes maiores, tendo presente a 7ª menor na sua constituição, onde a relação intervalar da 3ª maior para a 7ª é de um trítono.

O trítono causa sensação de tensão, motivo que o faz ser muito explorado pelos compositores quando querem gerar esta sensação naqueles que ouvem a música. O acorde que na escala maior diatônica possui o trítono é gerado a partir da quinta nota da escala. Tal acorde, por dar a sensação de movimento-tensão ao ouvinte, é chamado em harmonia funcional de acorde dominante.

O trítono é facilmente entendido se o formamos por intervalos de terças menores, resultando assim o acorde tétrade diminuto. Os intervalos são de tônica, terça menor, quinta diminuta e sétima diminuta, na ordem crescente, Dó, Mi bemol, Sol bemol e Si dobrado bemol.

Há boatos de que o intervalo de trítono era considerado um intervalo proibido pela Igreja Católica nas cerimônias religiosas, porém muitos estudiosos sérios afirmam que isso não passa de um mito.

Na música erudita e em muitos outros gêneros musicais, é muito comum o uso dos acordes como tríades. No entanto, se o acorde gerado a partir do quinto grau da escala maior for uma tétrade, ele inevitavelmente terá o trítono na sua constituição.

Todos os acordes diminutos possuem em sua formação o trítono e possuem dois trítonos se forem construídos no formato de tétrade, sendo os trítonos a distância intervalar da tônica do acorde para a quinta do mesmo e a distância da terça menor para a sétima diminuta, se o acorde diminuto for uma tétrade.

Exemplos de trítono podem ser encontrados em quase todas as músicas de quase todos os gêneros musicais. Músicas mais carregadas de tensão (como a 5ª Sinfonia, 1º Movimento de Beethoven) obviamente possuem mais trítonos ou outros intervalos que geram tensão em sua construção harmônico-melódica.

O trítono é um elemento essencial de alguns grupos de heavy metal, compondo a atmosfera musical que lhe é característica.[1]

Principal riff da canção "Black Sabbath" da banda britânica Black Sabbath. Este é um evidente exemplo de trítono G-C# que mostra o amplo uso desta progressão harmônica no heavy metal.

Não confundir trítono com o trinado que é equivalente a repetição rápida e alternada entre a nota em que se encontra o "tr" seguido por um mordente e sua superior.

É conhecido como "a nota do diabo".[2]

Referências

  1. ↑ Metal: A Headbanger's Journey. Documentário. Produção de Sam Dunn, Scot McFayden e Sam Feldman. Warner Home Video, 2005.
  2. ↑ «O que é o "som do diabo"?». mundoestranho.abril.com.br. Consultado em 17 de janeiro de 2013 

3. Maestro Rogerio Martins. 21 de maio de 2021. Complemento do texto sobre intervalos no acorde diminuto.

Ícone de esboço Este artigo sobre música é um esboço. Você pode ajudar a Wikipédia expandindo-o.

Read other articles:

Daftar Perdana Menteri Mesir

Perdana Menteri Republik Arab MesirLambang MesirPetahanaMoustafa Madbouly[1]sejak 7 Juni 2018GelarYang MuliaMasa jabatanTidak ada batasanPejabat perdanaNubar PashaDibentuk28 Agustus 1878Situs webwww.cabinet.gov.eg Mesir Artikel ini adalah bagian dari seri Politik dan KetatanegaraanRepublik Arab Mesir Konstitusi (sejarah) Pemerintahan Presiden (daftar) Abdel Fattah el-Sisi Perdana Menteri (daftar) Sherif Ismail Kabinet Legislatif Parlemen Dewan Perwakilan Rakyat Ketua (daftar) Ali...

 

 

Bernardo del Carpio

Bernardo del Carpio Bernardo del Carpio (juga dieja Bernaldo del Carpio) adalah pahlawan legendaris Spanyol pada Abad Pertengahan. Berbeda dengan El Cid, dia bukanlah tokoh yang nyata. Hingga akhir abad ke-XIX dan kerja keras Ramón Menéndez Pidal, dia dianggap sebagai pahlawan utama Spanyol Kristen abad pertengahan dan diyakini sebagai tokoh bersejarah. Kisah Bentuk paling awal dari legenda Bernardo ditemukan dalam Chronicon mundi karya Lucas de Tuy (1236), diikuti oleh Historia Gothica dar...

 

 

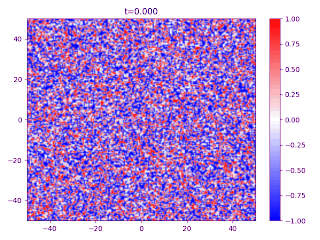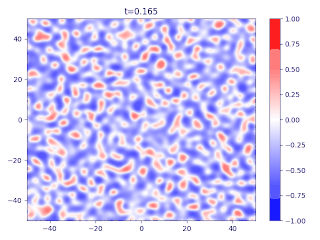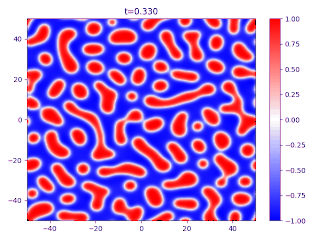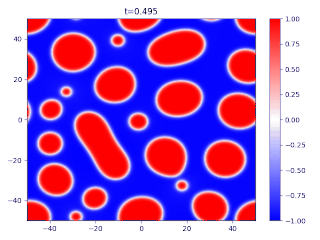
Cahn–Hilliard equation

The Cahn–Hilliard equation (after John W. Cahn and John E. Hilliard)[1] is an equation of mathematical physics which describes the process of phase separation, by which the two components of a binary fluid spontaneously separate and form domains pure in each component. If c {\displaystyle c} is the concentration of the fluid, with c = ± 1 {\displaystyle c=\pm 1} indicating domains, then the equation is written as ∂ c ∂ t = D ∇ 2 ( c 3 − c − ...

محمد عثمان (مغن)

محمد عثمان معلومات شخصية الميلاد سنة 1855[1]  محافظة القاهرة  تاريخ الوفاة 19 ديسمبر 1900 (44–45 سنة)[1]  مواطنة مصر  الحياة العملية المهنة مغني  تعديل مصدري - تعديل     لمعانٍ أخرى، طالع محمد عثمان (توضيح). محمد عثمان ولد سنة 1855 - توفي في 19 ديسمبر سنة 1900 ه�...

 

 

Itá, Santa Catarina

Municipality in South, BrazilItá, Santa CatarinaMunicipality FlagSealCountry BrazilRegionSouthStateSanta CatarinaMesoregionOeste CatarinensePopulation (2020 [1]) • Total6,129Time zoneUTC -3 Itá, Santa Catarina is a municipality in the state of Santa Catarina in the South region of Brazil.[2][3][4][5] See also List of municipalities in Santa Catarina References ^ IBGE 2020 ^ Divisão Territorial do Brasil (in Portuguese). Divisão...

 

 

غيدروتورف (نيزنيج نوفغورود)

غيدروتورف الإحداثيات 56°28′28″N 43°32′29″E / 56.474444444444°N 43.541388888889°E / 56.474444444444; 43.541388888889  تقسيم إداري  البلد روسيا[2][1]  عدد السكان  عدد السكان 7424 (1 يناير 2018)[3]  معلومات أخرى منطقة زمنية ت ع م+03:00  606425  رمز الهاتف 83144  رمز جيونيمز 561504  الم...

Canoe polo

Team sport played in kayaks Canoe poloHighest governing bodyInternational Canoe FederationNicknamesKayak Polo, PoloCharacteristicsTypeWaterEquipmentWater polo ball, buoyancy aid, helmet and face guard, goals, canoe polo kayak, paddle, spray deckPresenceOlympicNoWorld Games2005 – present Warm-up of the Italian national team during the European Canoe Polo Championship 2013 Canoe polo, also known as kayak polo, is one of the competitive disciplines of kayaking. The sport is ...

 

 

Sukarjo Wiryopranoto

Sukarjo Wiryopranoto Duta Besar Indonesia untuk Perserikatan Bangsa-Bangsa ke-4Masa jabatan1960–1962PresidenSoekarno PendahuluAli SastroamidjojoPenggantiL.N PalarDuta Besar Indonesia untuk Tiongkok ke-2Masa jabatan1956–1960PresidenSoekarno PendahuluArnold MononutuPenggantiSoekarni KartodiwirjoDuta Besar Indonesia untuk Italia ke-1Masa jabatan1952–1954PresidenSoekarno PenggantiSutan Mohammad RasjidDuta Besar Indonesia untuk Takhta Suci ke-1Masa jabatan1950–1952PresidenS...

 

 

Discovery Kids (Indian TV channel)

Indian television channel Television channel Discovery KidsCountryIndiaBroadcast areaIndian subcontinentHeadquartersMumbai, Maharashtra, IndiaProgrammingLanguage(s) Hindi Tamil Telugu Malayalam Kannada Picture format576i SDTVOwnershipOwnerWarner Bros. Discovery IndiaSister channelsSee List of channels owned by Warner Bros. Discovery IndiaHistoryLaunched7 August 2012LinksWebsiteDKids Discovery Kids is an Indian cable and satellite television channel operated by Warner Bros. Discovery India. Th...

Kirkuk District

A district in Iraq District in IraqKirkuk DistrictDistrictLocation of Kirkuk District within Kirkuk GovernorateCountry IraqGovernorateKirkuk GovernorateSeatKirkukArea • District3,525 km2 (1,361 sq mi)Highest elevation (Mavi dağ)1,138 m (3,734 ft)Population (2018)1,138,703 • Urban1,048,406 (92.1%) • Rural90,297 (7.9%)Time zoneUTC+3 (AST)Area code+964 50 Kirkuk District (Arabic: قضاء كركوك, Kurdish: قەز...

 

 

The Joy of Sect

Not to be confused with The Joy of Sets. 13th episode of the 9th season of The Simpsons The Joy of SectThe Simpsons episodeVarious residents of Springfield being forced by the Movementarians cult into growing and harvesting lima beans.Episode no.Season 9Episode 13Directed bySteven Dean MooreWritten bySteve O'DonnellProduction code5F23Original air dateFebruary 8, 1998 (1998-02-08)Episode featuresChalkboard gagShooting paintballs is not an art form[1]Couch gagTiny ve...

 

 

大字 (数字)

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています（詳細）。 数字の大字（だいじ）は、漢数字の一種。通常用いる単純な字形の漢数字（小字）の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券（「壱」が大字） 弐千円日本銀行券（「弐」が大字） 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Torremochuela

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Torremochuela – news · newspapers · books · scholar · JSTOR (April 2024) (Learn how and when to remove this message)Place in Castile-La Mancha, SpainTorremochuela, SpainTorremochuela, SpainShow map of Province of GuadalajaraTorremochuela, SpainShow map of Casti...

 

 

State Highway 50 (New Zealand)

Road in New Zealand This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: State Highway 50 New Zealand – news · newspapers · books · scholar · JSTOR (August 2015) (Learn how and when to remove this message) State Highway 50Route informationMaintained by NZ Transport AgencyLength91.5 km (56.9 mi...

 

 

كرة السلة في الألعاب الأولمبية الصيفية 2016

كرة السلة في الألعاب الأولمبية الصيفية 2016معلومات عامةجزء من الألعاب الأولمبية الصيفية 2016 الرياضة كرة السلة البلد البرازيل المكان صالة كاريوكا 1صالة الشباب رقم الطبعة 19 بتاريخ 2016 تاريخ البدء 6 أغسطس 2016 تاريخ الانتهاء 21 أغسطس 2016 المنظم الاتحاد الدولي لكرة السلة عدد المشارك�...

Indigo Tribe

DC comics organization This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. needs to be combed through and compared with the comic for removal of interpretive or synthesized phrases Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (November 2012) (Lear...

 

 

Newkirk Avenue–Little Haiti station

New York City Subway station in Brooklyn For the BMT Brighton Line station, serving the B and ​Q trains, see Newkirk Plaza station. New York City Subway station in Brooklyn, New York Newkirk Avenue–Little Haiti ​ New York City Subway station (rapid transit)Station platformStation statisticsAddressNewkirk Avenue & Nostrand AvenueBrooklyn, NYBoroughBrooklynLocaleFlatbush, East FlatbushCoordinates40°38′24″N 73°56′54″W / 40.639912...

 

 

قائمة البلديات في أشتورية

بلديات المقاطعة هنا قائمة ببلديات منطقة أشتورية (بالإسبانية: Asturias)‏, المصنفة على أنها إحدى مقاطعات إسبانيا. والتي تقع في الشمال الغربي لإسبانيا. الاسم السكان (2002) السكان (2014)[1] ألاندي 2,374 1,891 ألير 14,786 11,906 أمايفا 889 772 أفايلاس 83,511 82,568 بيلمونتي دي ميراندا 2,209 1,711 بايمينس 2,071 1,8...

المتحدون (فيلم)

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2023) المُتَحَدوُنChallengers (بالإنجليزية) الشعارمعلومات عامةالصنف الفني كوميديا درامية — فيلم رياضة — فيلم رومانسي تاريخ الصدور 18 أبريل 2024[1] (أستراليا، ‏نيوز�...

 

 

Ligue Rhône-Alpes de football

Ligue Rhône-Alpes de football Sigle LRAF Nom(s) précédent(s) Ligue du Lyonnais de football Sport(s) représenté(s) Football Création 1920 Disparition 2016 Président BARBET Bernard Affiliation FFF Site internet rhone-alpes.fff.fr modifier  La Ligue Rhône-Alpes de football est un organe fédéral dépendant de la Fédération française de football créé en 1920 et disparu en 2016 chargé d'organiser les compétitions de football au niveau de la région Rhône-Alpes. Créé en 192...