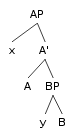
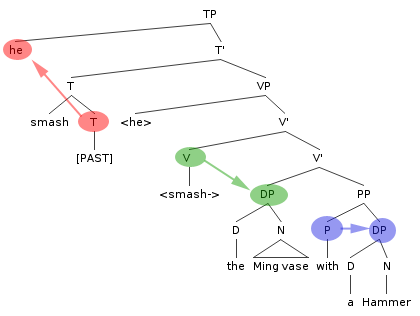
Teoria da regência e da ligação
|
Read other articles:

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. La mise en forme de cet article est à améliorer (janvier 2022). La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ». Forêt dégradée à Lahnberge, Allemagne : les sols sont lessivés par manque de couvert végétal, certains arbres perdent du terrain et semblent malades (photo d'Andreas Trepte). La dégradation des forêts est un processus da...

A.S. Livorno CalcioBerkas:Clubname = LivornoNama lengkapAssociazione SportivaLivorno Calcio S.p.A.JulukanAmaranto (Merah-Coklat)Labronici (Lighbourners) Le Triglie (The mullets) L'Unione (Persatuan)Berdiri1915StadionArmando Picchi,Livorno, Italia(Kapasitas: 19,238 (14,752 kompetisi UEFA))Ketua Aldo SpinelliManajer Davide NicolaLigaSerie A2012–13Serie B, 3rd (promosi) Kostum kandang Kostum tandang Kostum ketiga Associazione Sportiva Livorno Calcio adalah nama tim sepak bola Italia. Bermarkas...

Channapatna made toys An assortment of Channapatna toys and dolls Channapatna toys are a particular form of wooden toys and dolls that are manufactured in the town of Channapatna in the Ramanagara district of Karnataka state, India. This traditional craft is protected as a geographical indication (GI) under the World Trade Organization, administered by the Government of Karnataka.[1] As a result of the popularity of these toys, Channapatna is known as the Gombegala Ooru (toy-town) of ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

イスラームにおける結婚(イスラームにおけるけっこん)とは、二者の間で行われる法的な契約である。新郎新婦は自身の自由な意思で結婚に同意する。口頭または紙面での規則に従った拘束的な契約は、イスラームの結婚で不可欠だと考えられており、新郎と新婦の権利と責任の概要を示している[1]。イスラームにおける離婚は様々な形をとることができ、個�...

此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Large body of relatively still water For other uses, see Lake (disambiguation) and Lakes (disambiguation). Lac Gentau in the Ossau Valley of the Pyrenees, France Lake Michigan during a storm near the Ludington Lighthouse A lake is a naturally occurring, relatively large and fixed body of water on the Earth's surface. It is localized in a basin or interconnected basins surrounded by dry land.[1] Lakes lie completely on land and are separate from the ocean, although they may be connecte...

Italian politician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Giuseppe ...

Śrī Guru Tegh Bahadur (1º aprile 1621 – 11 novembre 1675) è stato il nono guru dei Sikh. Indice 1 Biografia 2 Note 3 Altri progetti 4 Collegamenti esterni Biografia Fu padre di Guru Gobind Singh. Guru Tegh Bahadur ji è conosciuto anche come Hind di Chadar ovvero salvatore dell'induismo, Guru Tegh Bahadur ji sacrificò la sua vita per salvare la religione induista sotto richiesta di alcuni pandit (sacerdoti hindu). Guru ji il 25 maggio del 1675, decise di andare ad Agra per parlare con ...

2022年肯塔基州聯邦參議員選舉 ← 2016年 2022年11月8日 (2022-11-08) 2028年 → 获提名人 蘭德·保羅 查爾斯·布克 政党 共和黨 民主党 民選得票 913,326 564,311 得票率 61.8% 38.2% 各縣結果保羅: 50–60% 60–70% 70–80% 80–90%布克: 50–60% 60–70% 选前聯邦參議...

ORF2 protein (exhibiting reverse transcriptase and endonuclease activity) from human LINE-1. Genetic structure of murine LINE1 and SINEs. Bottom: proposed structure of L1 RNA-protein (RNP) complexes. ORF1 proteins form trimers, exhibiting RNA binding and nucleic acid chaperone activity. Long interspersed nuclear elements (LINEs)[1] (also known as long interspersed nucleotide elements[2] or long interspersed elements[3]) are a group of non-LTR (long terminal repeat) ret...

The Last of Us Part II Publikasi29 Mei 2020Versi 1.09 (1r Juli 2021) GenreAksi-petualangan, survival horror, stealth actionKarakterEllie, Joel, Yara, Lev, Dina, Emily, Jesss, Tommy, Shamblers, Bloaters, Clickers, Stalkers, Runners, Abby, Maria, Nora, Marlene, Jerry, Owen, Mel, Manny, Isaac, Mike, Jordan, Whitney, Nick, Seth, JJ, Seraphites, Washington Liberation Front, Rattlers dan Rat King Latar tempatThe Last of Us universe LisensiLisensi proprietarium Bahasa Daftar Inggris, Italia, Jerman,...

دورة فرنسا المفتوحة 1988 رقم الفعالية 87 البلد فرنسا التاريخ 1988 الرياضة كرة المضرب الفعاليات دورة فرنسا المفتوحة 1988 - فردي السيدات، ودورة فرنسا المفتوحة 1988 - فردي الرجال، ودورة فرنسا المفتوحة 1988 - زوجي السيدات، ودورة فرنسا المفتوحة 1988 – زوجي رجال ...

Siege of Ruthven Barracks (1746)Part of the Jacobite rising of 1745Present-day view of Ruthven BarracksDate10–11 February 1746[1][2]LocationRuthven, Scotland, Great BritainResult Jacobite victory[1]Belligerents Jacobites Great BritainCommanders and leaders John Gordon[2] Terrance Molloy[2]Strength 300[2] UnknownCasualties and losses Unknown Unknown vteJacobite rising of 1745 Highbridge 1st Ruthven Prestonpans Culloden House 1st Carlisle...

Method of teaching reading and writing This article is about the method for teaching reading and writing. For the study of speech sounds, see Phonetics and Phonology. Children should practise phonics by reading books consistent with their developing phonic knowledge and skill; and, at the same time they should hear, share and discuss a wide range of high-quality books to develop a love of reading and broaden their vocabulary - National curriculum in England, 2014.[1] Part of a series ...

1992 studio album by Arisa MizukiArisa II: Shake Your Body for MeStudio album by Arisa MizukiReleasedOctober 1, 1992Recorded1992GenrePop, danceLength51:29LabelNippon ColumbiaProducerMotoki Funayama, Tetsuya Komuro, Takao Konishi, Arisa Mizuki (exec.), Yasuharu Ogura, Johny Taira (exec.)Arisa Mizuki chronology Arisa(1991) Arisa II: Shake Your Body for Me(1992) Arisa III: Look(1994) Singles from Arisa II: Shake Your Body for Me Too Shy Shy Boy!Released: May 27, 1992 Arisa II: Shake Your...

Men's individual foil at the 2018 Asian GamesVenueJakarta Convention CenterDate21 AugustCompetitors29 from 16 nationsMedalists Huang Mengkai China Nicholas Choi Hong Kong Cheung Ka Long Hong Kong Son Young-ki South Korea← 20142022 → Fencing at the2018 Asian GamesIndividual épéemenwomenTeam épéemenwomenIndividual foilmenwomenTeam foilmenwomenIndividual sabremenwomenTeam sabremenw...

English engineer, inventor of the Hovercraft This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Christopher Cockerell – news · newspapers · books · scholar · JSTOR (January 2023) (Learn how and when to remove this message) Christopher CockerellMemorial to Cockerell at Hythe, HampshireBorn(1910-06-04)4 June 1910...

الدوري الإنجليزي لكرة القدم 2017–18 تفاصيل الموسم دوري كرة القدم الإنجليزية البلد المملكة المتحدة البطل وولفرهامبتون واندررز الدوري الإنجليزي لكرة القدم 2016–17 دوري كرة القدم الإنجليزي 2018–19 تعديل مصدري - تعديل الدوري الإنجليزي لكرة القدم 2017–18 هو موسم م...

جائزة دينين الكبرى 2016 تفاصيل السباقسلسلة58. جائزة دينين الكبرىمسابقاتطواف أوروبا للدراجات 2016 1.HCكأس فرنسا لركوب الدراجات على الطريقالتاريخ14 أبريل 2016المسافات199٫6 كمالبلد فرنسانقطة البدايةدينيننقطة النهايةدينينالفرق20عدد المتسابقين في البداية155عدد المتسابقين في النه�...