Teorema de Parseval
|
Read other articles:

Rusli Marzuki SariaBiografiKelahiran26 Februari 1936 (88 tahun)Kamang Mudiak Data pribadiKelompok etnikOrang Minangkabau KegiatanPekerjaanPenyair Periode aktif1957 –Bekerja diHarian Haluan KeluargaPasangan nikahHanizar Musa (1963–) Orang tuaMardjuki Datuk Radjo Pangulu , Sarianun Penghargaan Penghargaan Penulis Asia Tenggara Rusli Marzuki Saria (lahir 26 Februari 1936)[1] adalah veteran pejuang kemerdekaan,[1][2] wartawan, sastrawan dan penyair...

14th President of Mexico (1792–1854) This article is about the Mexican politician. For the municipality named in his honor, see José Joaquín de Herrera (municipality). In this Spanish name, the first or paternal surname is de Herrera and the second or maternal family name is Ricardos. José Joaquín de HerreraPortrait of José Joaquín de Herrera14th President of MexicoIn office12 – 21 September 1844Preceded byAntonio López de Santa AnnaSucceeded byValentín Canali...

فواز الساجر معلومات شخصية تاريخ الميلاد سنة 1948 تاريخ الوفاة 1988 الحياة العملية المهنة أستاذ جامعي تعديل مصدري - تعديل فواز الساجر (1948 - 16 أيار 1988) مخرج مسرحي سوري، ولد في إحدى قرى منبج ناحية أبو قلقل في محافظة حلب.[1] حصل على الشهادة الثانوية الفرع الأدبي بتفوق ع...

ĉ Questa voce o sezione sugli argomenti matematica e storia non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Le note presenti si riferiscono unicamente ad un paragrafo e i collegamenti esterni sono tutti in inglese. Bibliografia assente Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti dei progetti di riferimento 1, 2. L'ingresso alla sezione 52 (LII) del Colosseo. Il siste...
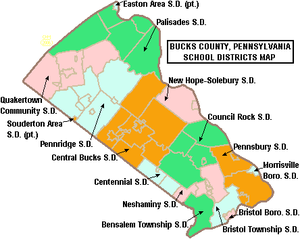
School district in Pennsylvania Quakertown Community School DistrictLocation of Quakertown Community School District in Bucks County, Pennsylvania Quakertown Community School District is a public school district located in Bucks County, Pennsylvania. The Quakertown Community School District covers 72 square miles[1] and serves the boroughs of Quakertown, Richlandtown, and Trumbauersville; as well as Haycock, Milford, and Richland Townships. Quakertown's mascot is the panther. Schools ...

Building located in Ahmedabad, India This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dada Harir Stepwell – news · newspapers · books · scholar · JSTOR (February 2014) (Learn how and when to remove this message) Bai Harir StepwellStepwell staircaseGeneral informationTown or cityAhmedabadCountryIndiaCoordinate...

Census-designated place in Berks and Lancaster counties in Pennsylvania, United States Census-designated place in Pennsylvania, United StatesMorgantown, PennsylvaniaCensus-designated placeOdd Fellows HallMorgantownShow map of PennsylvaniaMorgantownShow map of the United StatesCoordinates: 40°09′18″N 75°53′24″W / 40.15500°N 75.89000°W / 40.15500; -75.89000CountryUnited StatesStatePennsylvaniaCountiesBerks, LancasterTownshipsCaernarvon, CaernarvonArea[1&#...

Artikel ini bukan mengenai Kejuaraan Formula Dua, Kejuaraan Formula 2, atau Formula Dua. Seri GP2KategoriPengemudi tunggalNegara atau daerahInternasionalMusim pertama2005Musim terakhir2016Pembalap26Tim13KonstruktorDallaraPemasok mesinMecachromePemasok banPirelliJuara pembalap terakhir Pierre GaslyJuara tim terakhir Prema RacingSitus webgp2series.com Musim saat ini Seri GP2, GP2 kependekannya, adalah bentuk balap mobil roda terbuka yang diperkenalkan pada tahun 2005, setelah terjadinya penghen...

Major League Baseball team season 2008 Los Angeles DodgersNational League West ChampionsLeagueNational LeagueDivisionWestBallparkDodger StadiumCityLos AngelesRecord84–78 (.519)Divisional place1stOwnersFrank McCourtPresidentJamie McCourtGeneral managersNed CollettiManagersJoe TorreTelevisionFSN Prime TicketKCAL (9) Vin Scully, Charley Steiner, Steve LyonsRadioKABC Vin Scully, Rick Monday, Charley Steiner KHJ Jaime Jarrín, Pepe Yñiguez, Fernando Valenzuela ← 2007 Seasons 20...

Sports season2013 Big Ten Conference football seasonLeagueNCAA Division I FBS (Football Bowl Subdivision)SportFootballDurationAugust 30, 2013through January 2014Number of teams12TV partner(s)ABC, ESPN2, ESPN Inc., Big Ten Network, FOX (championship game)2014 NFL DraftTop draft pickTaylor Lewan (Michigan)Picked byTennessee Titans, 11th overallRegular SeasonSeason MVPBraxton MillerTop scorerBraxton MillerLeaders Division championsOhio StateLegends Division championsMichigan StateChampionship G...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of people pardoned by George H. W. Bush – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove this message) This article is part of a series aboutGeorge H. W. Bush Family Electoral history Pre-vice presidency U.S. Represe...

Berikut daftar Kepala Daerah dan Wakil Kepala Daerah di 24 kabupaten/kota di Sulawesi Selatan adalah: Kabupaten/Kota Foto Bupati/Wali Kota Bupati/Wali Kota Foto Wakil Bupati/Wali Kota Wakil Bupati/Wali Kota Mulai Menjabat Selesai Menjabat(Direncanakan) Ref KabupatenBantaengDaftar Bupati/Wakil Bupati Andi Abubakar(Penjabat) 26 September 2023 Menunggu pelantikan bupati dan wakil bupati terpilih hasil pemilihan umum Bupati Bantaeng 2024 [1] Kabupaten BarruDaftar Bupati/Wakil Bupati Suard...

McGaughey and Davies v USS Ltd and DirectorsCourtCourt of AppealDecidedMay 2022Citations[2023] EWCA Civ 873, [2022] EWHC 1233 (Ch)Court membershipJudge sittingAsplin LJKeywordsClimate litigation, derivative claim, Foss v Harbottle, Discrimination McGaughey and Davies v Universities Superannuation Scheme Ltd and Directors [2023] EWCA Civ 873 is a UK company law, climate litigation, and pension law case, seeking permission for a derivative claim to enforce duties of the directors of the UK univ...

Marvel comics character Not to be confused with his father, J. Jonah Jameson. Comics character John JamesonJohn Jameson as depicted in Web of Spider-Man Annual #3 (October 1987). Art by Don Perlin (pencils), Keith Wilson (inks), and Paul Becton (colors).Publication informationPublisherMarvel ComicsFirst appearanceThe Amazing Spider-Man #1 (March 1963)Created byJohn Jameson:Stan Lee (writer)Steve Ditko (artist)Man-Wolf:Gerry Conway (writer)Roy Thomas (artist)In-story informationAlter egoJohn J...

1983 film by K. Bhagyaraj For the TV series, see Mundhanai Mudichu (TV series). Mundhanai MudichuPosterDirected byK. BhagyarajWritten byK. BhagyarajProduced byM. KumaranM. SaravananM. BalasubramanianStarringK. BhagyarajUrvashiCinematographyAshok KumarEdited byA. SelvanathanMusic byIlaiyaraajaProductioncompanyAVM ProductionsRelease date 22 July 1983 (1983-07-22) Running time150 minutes[1]CountryIndiaLanguageTamil Mundhanai Mudichu (transl. Saree Knot) is a 1983 Ind...

Sprint CanadaFormerlyCall-Net EnterprisesIndustryTelecommunicationsFounded1993; 31 years ago (1993)Defunct2005; 19 years ago (2005)FateAcquired and mergedSuccessorRogers TelecomArea servedCanadaServiceslandline, long-distance, dial-up Internet access, email, GSM (via Fido) Sprint Canada was a Canadian telecommunications service provider active from 1993 until 2005, when it was acquired by Rogers Communications. It offered both residential and business servi...

4th SFFCC Awards December 12, 2005 Best Picture: Brokeback Mountain The 4th San Francisco Film Critics Circle Awards, honoring the best in film for 2005, were given on 12 December 2005. Winners Ang Lee, Best Director winner Heath Ledger, Best Actor winner Reese Witherspoon, Best Actress winner Kevin Costner, Best Supporting Actor winner Amy Adams, Best Supporting Actress winner Best Picture: Brokeback Mountain Best Director: Ang Lee - Brokeback Mountain Best Screenplay: Good Night, and Good ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of governors of Kandahar – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message) This is a list of the governors of the province of Kandahar, Afghanistan. Governor Period Extra Note Muhammad 'Amin Khan ?-18...

This is a list of the orders, medals and merit awards of Rwanda. Republic of Rwanda The Republic of Rwanda's honours system consists of orders and medals awarded for exemplary service to the nation.[1] Orders and Medals Acronym RDF Order of Honour OH National Liberation Medal LM Campaign Against Genocide Medal (Umurinzi Medal) CGM Order of Bravery Medal OB Exemplary Performance Medal EPM Defence Superior Service Medal DSSM Joint Command Superior Medal JCM Land Forces Superior Service...

En tibetansk buddhistisk målning som ska symbolisera samsara Samsara kommer från sanskrit och betyder att flyta ihop, att passera genom olika stadier eller att vandra. I religioner med indiskt ursprung kan samsara enklast översättas som kretslopp [av död och återfödelse].[1] Advaita vedanta I advaita vedanta betraktas samsara som fundamentalt just en illusion (maya). Samsara i hinduismen Inom hinduismen är det själen som vandrar, dvs återföds (själavandring). Vissa former av hindu...

















![{\displaystyle \sum _{n=-\infty }^{\infty }|x[n]|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|X(e^{j\phi })|^{2}d\phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/159a2b69daf2450f0a702fcebc220f87a7062e57)
![{\displaystyle \sum _{n=0}^{N-1}|x[n]|^{2}={\frac {1}{N}}\sum _{k=0}^{N-1}|X[k]|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd01ef048644b8295d7e2332488c2013ec04b742)






![{\displaystyle =\int _{-\infty }^{\infty }f(t)\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }F(w)e^{iwt}dw\right]dt=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b7c79b6b423956059c85248e4d2a1406f6b898f)




![{\displaystyle ={\frac {1}{2\pi }}\int _{-\infty }^{\infty }F(w)\left[\int _{-\infty }^{\infty }f(t)e^{iwt}dt\right]dw=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20f3978176cb21f252c5008d6eb8803e8853ffa7)


