Teorema de Goodstein
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Basilika di Biara Val-Dieu Biara Val-Dieu Biara Val-Dieu adalah sebuah kompleks biara dan basilika Katolik yang dikelola oleh ordo Sistersien di Wallonia di lembah Berwinne dekat Aubel di Pays de Herve,provinsi Liège, Belgia. Sejarah Pada tahun 1216 sejumlah kecil biarawan dari Biara Hocht di Lanaken, dekat Maastricht, menetap di lembah tak berpenghuni yang menjadi perbatasan antara Kadipaten Limburg dan wilayah Dalhem; mereka menyebut pemukiman mereka Vallis Dei (Prancis: Val-Dieucode: fr i...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Judi daring – berita · surat kabar · buku · cendekiawan · JSTOR Judi Online adalah jenis perjudian yang dilakukan di Internet. ini termasuk Poker Virtual, Kasino, dan Taruhan Olahraga (Sportbook). Lokasi...

1977 United States dramatic television series This article is about the 1977 American television series that aired on CBS. For the 1984–1991 American television series that aired on NBC, see Hunter (1984 American TV series). For other television series, see Hunter (disambiguation). HunterGenreForeign intrigueCreated byWilliam BlinnStarringJames FranciscusLinda EvansRalph BellamyOpening themeRichard ShoresEnding themeRichard ShoresComposersRichard ShoresRichard Markowtiz (one episode)Country...

Serie D 2004-2005 Competizione Serie D Sport Calcio Edizione 57ª Organizzatore Lega Nazionale Dilettanti -Comitato per l'attività Interregionale Luogo Italia Partecipanti 164 Formula 9 gironi all'italiana Sito web lnd.it Risultati Vincitore Bassano Virtus(1º titolo) Altre promozioni CuneoCanzesePergocremaRietiFolignoReal MarcianiseGallipoliModica Retrocessioni (le squadre scritte in corsivo sono poi state ripescate)Valle d'Aosta Aosta-Sarre, Versilia 98Borgosesia, NoveseRobbio, Spar...

Josef Suk Rekam medali Kompetisi seni rupa Mewakili Cekoslowakia Permainan Olimpiade 1932 Los Angeles Musik Josef Suk (4 Januari 1874 – 29 Mei 1935) adalah seorang komponis dan pemain biola Ceko. Ia belajar di bawah bimbingan Antonín Dvořák, yang putrinya ia nikahi.[1] Referensi Kutipan ^ Josef Suk. Olympedia. Diakses tanggal 26 July 2020. Sumber Černušák, Gracián (ed.) (1965). Československý hudební slovník II. M-Ž (dalam bahasa Cheska). Prague...
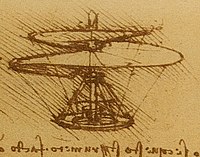
Cet article est une ébauche concernant la peinture. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Croquis d'un lion (1980), encre de Chine sur papier, par Frans Koppelaar. Croquis de l'idée d'une machine volante (vis aérienne), par Léonard de Vinci. Croquis de nu. Un croquis est un dessin fait rapidement, à main levée, sans recherche de détails dans le but de dégager à grands traits, l'essentiel du su...
Caucasian ethnic group indigenous to Georgia This article is about the Caucasian ethnic group. For the inhabitants of Georgia, see Demographics of Georgia (country). For the inhabitants of the US state, see Demographics of Georgia (U.S. state). For other uses, see Georgian (disambiguation). Georgians ქართველები KartvelebiThe Georgian kings, queens consort and the Catholicos-Patriarch depicted on a Byzantine-influenced fresco[a] wearing Byzantine dress at the Gelati...

Multi-use stadium in Vientiane, Laos New Laos National Stadiumສະໜາມກິລາແຫ່ງຊາດຫຼັກ16Interior of the stadium on a matchdayLocationXaythany, Vientiane Prefecture, LaosCoordinates18°3′43″N 102°42′14″E / 18.06194°N 102.70389°E / 18.06194; 102.70389OwnerLao government caretaker Lao Football FederationCapacity25,000Field size95 by 60 mSurfaceGrass TrackConstructionOpened2009Main contractorsShanghai Construction GroupTenants...

Season of television series Season of television series MasterChef JuniorSeason 1Promotional poster for season 1, featuring (2nd row, L to R) judges Graham Elliot, Joe Bastianich, and Gordon RamsayJudges Joe Bastianich Graham Elliot Gordon Ramsay No. of contestants12WinnerAlexander WeissRunner-upDara Yu No. of episodes7ReleaseOriginal networkFoxOriginal releaseSeptember 27 (2013-09-27) –November 8, 2013 (2013-11-08)Season chronologyNext →Season 2 The first season of th...

KaramelGenreKomediCeritaN.I.K.SutradaraIndrayanto KurniawanPemeran Syahla Anstasya A. Kanaya Gleadies Samuel Wlater Daren Rafid Khairan Shofia Shireen Penggubah lagu temaBemby NoorLagu pembukaHey Teman oleh Ellyn ClarissaPenata musikStevenNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim1Jmlh. episode4ProduksiProduserLeo SutantoSinematografiGatot Avia NugrohoPenyunting Danny A.W. Teddy Gunawan Pengaturan kameraMulti-kameraRumah produksiSinemArtDistributorSurya Citra MediaRilis...

Komal JhaKomal Jha pada film Mr. MBALahir15 Maret 1987 (umur 37)Ranchi, Bihar, India (sekarang bagian dari Jharkhand, India)Tempat tinggalMumbai, Maharashtra, India Dubai, Uni Emirat ArabKebangsaanIndiaPendidikanTeknik sipilAlmamaterB.E – Sipil dari MSRIT, BangalorePekerjaanArtis, teknik sipil, penulisTahun aktif2010 – sekarangSitus webiamkomaljha.com Komal Jha (lahir 15 Maret 1987) adalah seorang aktris film dan juga seorang penulis asal India. Komal Jha merupakan lulusan tekn...

Pintu masuk Akademi Gerejawi Kepausan. Kolese Romawi, yang juga disebut Kolese Kepausan di Roma, adalah institusi yang didirikan dan dikelola di Roma untuk pendidikan para calon rohaniwan Gereja Katolik. Biasanya banyak yang diperuntukkan bagi pelajar berkebangsaan tertentu. Perguruan tinggi adalah asrama tempat para siswa mengikuti latihan kesalehan seminari yang biasa, belajar secara pribadi, dan meninjau mata pelajaran yang diajarkan di kelas. Di beberapa perguruan tinggi terdapat kursus p...

Ode (dari bahasa Yunani Kuno: ᾠδή, translit. ōdḗ ) adalah jenis sajak lira . Ini adalah puisi terstruktur yang memuji atau memuliakan suatu peristiwa atau individu, menggambarkan alam secara intelektual dan juga emosional. Ode klasik disusun dalam tiga bagian utama: strophe, antistrof, dan epode . Bentuk ode yang berbeda lainnya, seperti ode homostrofik dan ode tak beraturan. Ode atau oda adalah puisi lirik berisikan semangat pujaan dalam nada agung dan tema serius. Ode berasa...

Italian mathematician (1906–1985) Bruno De FinettiBorn(1906-06-13)13 June 1906Innsbruck, Austria-HungaryDied20 July 1985(1985-07-20) (aged 79)Rome, ItalyNationalityItalianAlma materPolitecnico di MilanoKnown forDe Finetti's theoremScientific careerInstitutionsItalian National Institute of StatisticsAssicurazioni GeneraliUniversity of TriesteUniversity of PaduaSapienza University of Rome Bruno de Finetti (13 June 1906 – 20 July 1985) was an Italian probabilist statistician a...
C2 1000 metriBerlino 1936 Informazioni generaliLuogoBacino di Grünau Periodo8 agosto 1936 Partecipanti5 da 5 nazioni Podio Vladimír SyrovátkaJan Brzák-Felix Cecoslovacchia Rupert WeinstablKarl Proisl Austria Warren SakerHarvey Charters Canada Edizione precedente e successiva Prima apparizione Londra 1948 Voce principale: Canoa/kayak ai Giochi della XI Olimpiade. Canoa/kayak a Berlino 1936 Velocità Canadese C1 1000 m uomini C2 1000 m uomini C2 10000 m uomini K...

Peter Fleischmann 2019 Peter Fleischmann (Zweibrücken, 26 luglio 1937 – Potsdam, 11 agosto 2021[1]) è stato un regista tedesco, esponente della corrente del cosiddetto Nuovo cinema tedesco. Indice 1 Biografia 2 Filmografia parziale 3 Note 4 Bibliografia 5 Altri progetti 6 Collegamenti esterni Biografia Figlio di un giudice, fin da bambino è stato incoraggiato a coltivare interessi culturali e ha seguito lezioni di musica. Assieme ai suoi tre fratelli suonava in quartetto e nel fr...

Это статья об австрийском эрцгерцоге. О британской рок-группе см. статью «Franz Ferdinand». Франц ФердинандFranz Ferdinand Эрцгерцог и Кронпринц Австрийский 19 мая 1896 года — 28 июня 1914 года Монарх Франц Иосиф I Предшественник Карл Людвиг (1889—1896) Преемник Карл (1914—1916) Рождение 18 декабр�...

No debe confundirse con ط. ← ṭāʾ ʿayn → Ẓāʾ ﻅ ـﻆFinalـﻈMediaﻇInicial HistoriaOrigen 𐤈طظEquivalentes (en sudarábigo)Alfabeto árabe خ ح ج ث ت ب ا ص ش س ز ر ذ د ق ف غ ع ظ ط ض ي و ه ن م ل ك La ẓāʾ o ḏ̣āʾ (en árabe ﻇﺎء, ẓāʾ [ðˤaːʔ]) es la decimoséptima letra del alfabeto árabe. Representa un sonido fricativo, alveolar, sonoro y velarizado,[1] /ðˁ/ o /zˁ/. En la numeración abyad tiene generalm...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Vigor Lamezia. Vigor Lamezia CalcioStagione 2010-2011Sport calcio Squadra Vigor Lamezia Allenatore Francesco Massimo Costantino Presidente Paolo Mascaro Lega Pro Seconda Divisione9º posto nel girone C. Maggiori presenzeCampionato: De Luca (28) Miglior marcatoreC...

American baseball player (born 1979) Baseball player Colby LewisLewis with the Texas RangersPitcherBorn: (1979-08-02) August 2, 1979 (age 45)Bakersfield, California, U.S.Batted: RightThrew: RightProfessional debutMLB: April 1, 2002, for the Texas RangersNPB: 2008, for the Hiroshima Toyo CarpLast appearanceNPB: 2009, for the Hiroshima Toyo CarpMLB: October 1, 2016, for the Texas RangersMLB statisticsWin–loss record77–72Earned run avera...


















































































































