Rio Cavalum

Rio Cavalum
Rio Cavalum
Quedas d'agua do rio Cavalum em Penafiel. 1920
Nascente Casais Novos
Foz rio Sousa
País(es) Portugal Portugal

O rio Cavalum é um rio que nasce em Portugal, no concelho de Penafiel, perto da freguesia de Croca, na localidade de Casais Novos. É um afluente do rio Sousa, e pertence à bacia hidrográfica do Rio Douro.

A presa identificada como nascente do rio Cavalum, está envolta em silvados. A partir daí o Cavalum, que mais parece um pequeno rego de água, está encanado, atravessando alguns campos. Curiosamente, não é dos tempos actuais a atitude de encanar o rio Cavalum nas proximidades da sua nascente. Vários troços do rio já foram encanados no passado, atravessando subterraneamente alguns campos através de “minas” feitas totalmente em pedra.   

Decorre um projecto de limpeza e requalificação parcial das margens do Rio Cavalum, iniciado em Agosto de 2010, numa parceria com a Penafiel Verde, a ARH – Administração da Região Hidrográfica e o Instituto do Emprego e Formação Profissional.   

A Ministra do Ambiente valorizou e elogiou publicamente este projecto, que pretende limpar os 17 km de extensão do rio, devolvendo o Cavalum aos Penafidelenses.

Read other articles:

1914 Yale Bulldogs football team

American college football season 1914 Yale Bulldogs footballConferenceIndependentRecord7–2Head coachFrank Hinkey (1st season)Home stadiumYale FieldYale BowlSeasons← 19131915 → 1914 Eastern college football independents records vte Conf Overall Team W   L   T W   L   T Army   –   9 – 0 – 0 Harvard   –   7 – 0 – 2 Washington & Jefferson   –   10 – 1 – 0 D...

 

Rai Radio Kids

Rai Radio KidsPaese Italia Linguaitaliano Data di lancio12 giugno 2017 EditoreRai Sito webwww.raiplaysound.it/radiokids/ DiffusioneTerrestreDABCanali 12B · 12D RaiRAI Mux ARai Radio Kids (Italia)(DVB-T - HbbTV - FTA)Canale 707 SatellitareSky ItaliaEutelsat Hot Bird 13FRai Radio Kids (DVB-S2 · FTA)11766 - V - 29900 - 3/4Canale 8831 TivùsatEutelsat Hot Bird 13FRai Radio Kids (DVB-S2 · FTA)11766 - V - 29900 - 3/4Canale 639 Eutelsat 5 West BRai Radio Kids (DVB-S2 · F...

 

Rico Lewis

Rico Lewis Informasi pribadiNama lengkap Rico Mark Lewis[1]Tanggal lahir 21 November 2004 (umur 19)[2]Tempat lahir Manchester, InggrisTinggi 169 cm (5 ft 7 in)[2]Posisi bermain Bek kananInformasi klubKlub saat ini Manchester CityNomor 82Karier junior0000–2022 Manchester CityKarier senior*Tahun Tim Tampil (Gol)2022– Manchester City 6 (0)Tim nasional‡2019–2020 Inggris U-16 4 (0)2021– Inggris U-18 7 (1)2021– Inggris U-19 3 (0) * Penampilan...

Buriano (Castiglione della Pescaia)

BurianofrazioneBuriano – VedutaPanorama di Buriano LocalizzazioneStato Italia Regione Toscana Provincia Grosseto Comune Castiglione della Pescaia TerritorioCoordinate42°50′44″N 10°59′20″E / 42.845556°N 10.988889°E42.845556; 10.988889 (Buriano)Coordinate: 42°50′44″N 10°59′20″E / 42.845556°N 10.988889°E42.845556; 10.988889 (Buriano) Altitudine184 m s.l.m. Abitanti178 (2011) Altre informazioniCod. post...

 

Tiuna

Tiuna UR-53AR50 Tiuna dengan atap ditutup Jenis Light Utility Vehicle Negara asal Venezuela Sejarah pemakaian Masa penggunaan 2004 - Present Sejarah produksi Produsen CENARECA Biaya produksi $69,767.44 (USD) / BsF. 142.857,00 (VEF) (basic unit) Diproduksi July 20, 2004 – present Spesifikasi Berat 2 tons Panjang 4.92 meters Awak 9 (termasuk pengemudi) Jenis Mesin General Motors Vortec V8 5.3 litre Transmisi 5-kecepatan Suspensi beroda Tiuna UR-53AR50 adalah kendaraan mil...

 

Libya–North Korea relations

Bilateral relationsLibya–North Korea relations North Korea Libya Libya–North Korea relations (Korean: 리비아-조선민주주의인민공화국 관계, Arabic: العلاقات بين ليبيا وكوريا الشمالية) are relations between North Korea and Libya. North Korea established formal diplomatic relations with Muammar Gaddafi regime in Libya in 1974. The North Korean government maintains an embassy in Tripoli. In the 1970s and 1980s, the Libyan government under Muammar ...

Siumut

Siumut SiumutKetua umumKim KielsenDibentuk29 July 1977Kantor pusatNuuk, Sermersooq, GreenlandSayap pemudaPemuda SiumutIdeologiDemokrasi sosialKemerdekaan Greenland[1]EuroskeptikPosisi politikTengah-kiri[2]Afiliasi EropaTidak adaAfiliasi internasionalTidak adaAfiliasi NordikSAMAKWarnaMerahInatsisartut11 / 31 Munisipalitas39 / 73 Folketing(kursi Greenland)0 / 2 Situs webhttp://www.siumut.gl/ Siumut (secara harfiah berarti ke depan) adalah partai politik berhaluan demokrasi ...

 

赫瓦贾·纳齐姆丁

His Excellency赫瓦贾·纳齐姆丁爵士খাজা নাজিমুদ্দীন خواجہ ناظِمُ الدّین‬‎CIE, KCIE摄于1948年第2任巴基斯坦總理任期1951年10月17日—1953年4月17日君主佐治六世伊莉沙白二世总督古拉姆·穆罕默德前任利雅卡特·阿里·汗继任Mohammad Ali Bogra（英语：Mohammad Ali Bogra）第2任巴基斯坦總督（英语：Governor-General of Pakistan）任期1948年9月14日—1951年10月17日君�...

 

中華民國國軍中的中共間諜列表

 本表是動態列表，或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源，曾潛伏於中華民國國軍、被中國共產黨聲稱或承認，或者遭中華民國政府調查審判，為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準，正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Bleach

Untuk kegunaan lain, lihat Bleach (disambiguasi). BleachVolume pertama Bleach (diterbitkan di Jepang oleh Shueisha pada tanggal 5 Januari 2002) menampilkan Ichigo Kurosaki.ブリーチ(Burīchi)GenrePetualangan, supernatural[1] MangaPengarangTite KuboPenerbitShueishaPenerbit bahasa InggrisAUS Madman EntertainmentNA Viz MediaUK Viz MediaPenerbit bahasa IndonesiaM&C!ImprintJump ComicsMajalahWeekly Shōnen JumpMajalah bahasa InggrisNA Shonen Jump (sebelumnya) Weekly Shonen JumpDemogr...

 

Igor Dodon

President of Moldova from 2016 to 2020 Igor DodonDodon in 2019Leader of the Party of SocialistsIncumbentAssumed office 23 March 2024Preceded byHimself (as Executive Secretary)In office30 December 2020 – 18 December 2021Preceded byZinaida GreceanîiSucceeded byVlad Batrîncea (as Executive Secretary)In office18 December 2011 – 18 December 2016Preceded byVeronica AbramciucSucceeded byZinaida GreceanîiMember of the Moldovan ParliamentIn office23 July 2021 – ...

 

Пиетизм

Шпенер. Мемориальная доска на церкви, где проповедовал Шпенер. Пиети́зм (нем. Pietismus ← лат. pietas «благочестие»[1]) — изначально движение внутри лютеранской церкви, характеризующееся приданием особой значимости личному благочестию, религиозным переживаниям вер...

.nz

Internet country code top-level domain for New Zealand .nzIntroduced19 January 1987TLD typeCountry code top-level domainStatusActiveRegistryInternetNZIntended useEntities connected with New ZealandActual usePopular in New ZealandRegistered domains750,200 (September 2022)[1]Registration restrictionsNo restrictions under most second-level names; a few are moderated meaning that eligibility is checked before registration is grantedStructureNames are registered at the second level or at t...

 

How Do You Do It

How Do You Do It Gerry & the Pacemakers Veröffentlichung 14. März 1963 Länge 1:59 Genre(s) Pop Autor(en) Mitch Murray Album Don’t Let the Sun Catch You Crying (US-Album) Coverversion 1962 The Beatles How Do You Do It (englisch für: Wie machst Du das) ist ein Lied der britischen Band Gerry & the Pacemakers, das 1963 als Single veröffentlicht wurde. Die Beatles nahmen das Lied vor Gerry and the Pacemakers auf, veröffentlichten es aber erst 1995 auf ihrem Kompilationsalbum Antho...

 

Circolo Eridano

Circolo EridanoCanottaggio Segni distintiviColori sociali azzurro, bianco e rosso Dati societariCittàTorino Paese Italia ConfederazioneWorld Rowing (FISA) Fondazione1864 PresidenteLuigi Tartaglino Impianto sportivosul fiume Po Palmarèswww.circoloeridano.it Il Circolo Eridano dal fiume Po Il Circolo Eridano dall'ingresso su corso Moncalieri Il salone interno Un dettaglio del dipinto di Giuseppe Bozzalla Una porzione dell'hangar interno Il dehor esterno Il Circolo Eridano è uno dei più...

Alastair Fothergill

Questa voce sull'argomento registi britannici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Alastair Fothergill Alastair Fothergill (Londra, 10 aprile 1960) è un regista, produttore cinematografico e produttore televisivo britannico. Carriera The Really Wild Show (1986) Wild Britain (1987) Reefwatch (1988) Wildlife on One (1988-1992) Le sfide della vita (1990) Life in the Freezer (1993) Natural World (1998) - (1 ep.) The Blue Planet (2001) Going Ap...

 

Politics of Peru

Politics of Peru Constitution Executive President of PeruDina Boluarte Vice Presidents of PeruVacant (1st)Vacant (2nd) Prime Minister of PeruGustavo Adrianzén CabinetMinistries Legislature Congress of the Republic President Eduardo Salhuana Judiciary Supreme Court of the RepublicPresident Javier Arévalo Vela [es] Superior Courts of JusticeCourts of First InstanceCourts of Peace Autonomies National Board of Justice Constitutional Court Public Ministry Office of the Public Defen...

 

Jerusalem during the Byzantine period

Jerusalem Saint Peter in Gallicantu model of the Byzantine cityDuring the Byzantine period, in the years between Constantine the Great's rise to power (324 AD) and the conquest of Jerusalem by the Rashidun Caliphate in 637, Jerusalem was under the control of the Byzantine Empire. The essential change in the character and status of the city, compared to the Roman period, was its transformation from a pagan city to a Christian city. The Byzantine rule developed the Roman colony Aelia Capitolin...

八重の桜

大河ドラマ > 八重の桜この記事はプロジェクト:大河ドラマの編集方針を採用しています。編集される方はご一読下さい。 八重の桜ジャンル テレビドラマ時代劇脚本 山本むつみ吉澤智子三浦有為子演出 加藤拓 ほか出演者 綾瀬はるか（以下五十音順）秋吉久美子芦名星綾野剛池内博之池田成志市川染五郎市川実日子稲森いずみ伊吹吾郎榎木孝明及川光博岡田義徳�...

 

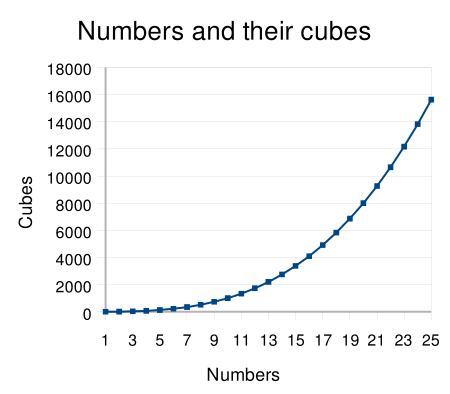
Cubo perfetto

Un cubo perfetto è un qualsiasi numero naturale la cui radice cubica corrisponde ad un numero intero. y=x³, per valori interi 1≤x≤25. In aritmetica e algebra, il cubo di un numero n è la sua terza potenza, cioè il risultato della moltiplicazione del numero per sé stesso tre volte: n3 = n × n × n. Si tratta anche della formula per calcolare il volume di un cubo il cui lato ha una lunghezza pari a n. Da qui il nome. La funzione inversa di trovare il numero il cui cubo è n è...