Propriedades de disjunção e existência
|
Read other articles:

Grand Prix Malaysia 2018Detail lombaLomba ke 18 dari 19Grand Prix Sepeda Motor musim 2018Tanggal4 November 2018Nama resmiShell Malaysia Motorcycle Grand Prix[1]LokasiSepang International Circuit, Sepang, Selangor, MalaysiaSirkuitFasilitas balapan permanen5.543 km (3.444 mi)Penonton103,984MotoGPPole positionPembalap Marc Márquez[N 1] HondaCatatan waktu 2:12.161 Putaran tercepatPembalap Álex Rins SuzukiCatatan waktu 2:00.762 di lap 5 PodiumPertama Marc M�...
نابانوش الإحداثيات 41°44′54″N 74°22′22″W / 41.748333333333°N 74.372777777778°W / 41.748333333333; -74.372777777778 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة أولستر خصائص جغرافية المساحة 3.224768 كيلومتر مربع3.226253 كيلومتر مربع (1 أبريل 2010) ارتفا...

Michael MannMann di Comic-Con International 2014.LahirMichael Kenneth Mann5 Februari 1943 (umur 81)Chicago, Illinois, A.S.Tempat tinggalLos Angeles, California, ASChicago, Illinois, ASKebangsaanAmerikaNama lainMichael K. MannAlmamaterUniversitas Wisconsin-MadisonTahun aktif1968–sekarangKota asalChicago, IllinoisSuami/istriSummer Mann (1974–sekarang; 4 anak)PenghargaanBAFTA Award untuk Film Terbaik2005 The Aviator NBR Award untuk Sutradara Terbaik2004 CollateralPrimeti...

Halaman ini berisi artikel tentang kuil di kota Sakurai. Untuk kuil bernama sama, lihat Ōmiwa Shrine (disambiguasi). Ōmiwa jinja大神神社Torii besar di depan Gunung MiwaAgamaAfiliasiShintoDewaŌmononushiŌnamuchiSukunahikona-no-kamiGunung MiwaLokasiLokasi1422 Miwa, Sakurai-shi, Nara-kenShown within JepangKoordinat34°31′44″N 135°51′10″E / 34.52889°N 135.85278°E / 34.52889; 135.85278Koordinat: 34°31′44″N 135°51′10″E / 34.52889°...

Sebuah parasit ikan, isopoda Cymothoa exigua, menggantikan lidah dari seekor Lithognathus Dalam biologi evolusioner, parasitisme adalah hubungan antar spesies, di mana satu organisme, parasit, hidup pada atau dalam organisme lain.[1] Seperti predasi, parasitisme adalah sebuah jenis interaksi konsumen-sumber daya.[2] Catatan Referensi ^ Poulin 2007, hlm. 4–5. ^ Getz, W. M. (2011). Biomass transformation webs provide a unified approach to consumer-resource modelling. Ecol...

Cet article est une ébauche concernant une commune du Puy-de-Dôme. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour vous aider. Consultez également la page d’aid...

ZeniMax Media Inc.JenisPrivateIndustriIndustri permainan videoDidirikan1999; 25 tahun lalu (1999)PendiriChristopher WeaverRobert A. AltmanKantorpusatRockville, Maryland, ASTokohkunciRobert A. Altman(ketua, CEO)James L. Leder(presiden, COO)Cindy L. Tallent(EVP, CFO)Total ekuitasUS$2,5 miliar[1] (2016)Karyawan1,500+ (2017)AnakusahaArkane StudiosBethesda Softworksid SoftwareMachineGamesTango GameworksZeniMax Online StudiosSitus webzenimax.com ZeniMax Media Inc. adalah...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (ديسمبر 2018) لمعانٍ أخرى، طالع استراحة (توضيح). استراحة في العمل (بالإنجليزية: Break) ه...

Азиатский барсук Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мле�...

S-Bahn Zúrich Unidad de la SBB-CFF-FFS prestando servicio en la línea S7 de S-Bahn Zúrich.LugarÁrea abastecida Cantón de Zúrich, Cantón de Argovia*, Cantón de Schaffhausen*, Cantón de Schwyz*, Cantón de Turgovia*, Alemania* *(Sólo zonas limítrofes)DescripciónTipo Tren de cercanías (S-Bahn)Inauguración Mayo de 1990Estaciones principales Zúrich, Winterthur, Thalwil, Uster, Dietikon, Zúrich-Oerlikon, Pfäffikon SZCaracterísticas técnicasLongitud red 380 kmEstaciones 171Explota...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2012. VanadjouDesaNegara ComorosPulauGrande ComorePopulasi (1991) • Total1.377Zona waktuUTC+3 (EAT) Vanadjou adalah sebuah desa atau perkampungan di pulau Komoro Besar di Komoro. Menurut hasil dari sensus pada tahun 1991 desa ini memiliki...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Štadión pod Zoborom – news · newspapers · books · scholar · JSTOR (November 2016) (Learn how and when to remove this message) Štadión pod ZoboromUEFA LocationNitra, SlovakiaCoordinates48°19′19″N 18°05′15″E / 48.3218565°N 18.087506...

Political application of the Christian doctrine of Paul of Tarsus Corporatism Concepts Corporate group Body politic Organicism Solidarity Structural functionalism Schools Christian Conservative Fascist Liberal Nationalistic Social Solidarist Statist Tripartite People Aristotle Durkheim Hegel Khaldūn Mill Müller Mussolini Plato Paul the Apostle Salazar Spann Tönnies Vargas Related articles Consociationalism Fascism Gemeinschaft and Gesellschaft Guild Guild socialism Political philosophy Pol...

2017 song by Lizzo Truth HurtsSingle by Lizzofrom the album Cuz I Love You (Deluxe) ReleasedSeptember 19, 2017 (original)March 22, 2019 (Re-released)Recorded2017GenreTraphip hoppopLength2:53Label Atlantic Nice Life Songwriter(s) Melissa Jefferson Eric Frederic Jesse Saint John Steven Cheung Amina Bogle-Barriteau Producer(s) Ricky Reed Tele (co.) Lizzo singles chronology Water Me (2017) Truth Hurts (2017) Fitness (2017) Audio samplefilehelpMusic videoTruth Hurts on YouTube Truth Hurts is a son...

DC Comics character Comics character AtomAl Pratt / Atom as depicted in Adventure Comics vol. 2 #1 (May 1999). Art by Dave Johnson.Publication informationPublisherDC ComicsFirst appearanceAll-American Comics #19 (October 1940)Created by Bill O'Connor Ben Flinton In-story informationAlter egoAlbert Al PrattSpeciesMetahumanTeam affiliationsJustice Society of AmericaAll-Star SquadronBlack Lantern CorpsAbilities Superhuman strength, stamina, durability, and speed Atomic punch Radiation immunity E...

Anak-anak sekolah di AS melakukan lompat lambai Lompat lambai adalah latihan lompat fisik yang dilakukan dengan melompat ke posisi dengan kaki terbuka lebar dan tangan mengarah ke atas, terkadang dengan tepukan, dan lalu kembali ke posisi dengan kaki rapat dan lengan di samping. Variasi dan kemajuan Latihannya bisa dibuat lebih atau kurang intens dengan variasi yang berbeda-beda. Secara umum, jongkok yang lebih dalam akan membuat lompatan menjadi lebih sulit, meskipun tidak menghasilkan keti...

В Википедии существуют статьи о других людях с именем Станислав и фамилией Лещинский. Станислав Лещинскийпол. Stanisław Leszczyński Герцог Лотарингии и Бара 9 июля 1737 — 23 февраля 1766 Предшественник Франциск III Преемник титул упразднён Король Польши и Великий князь Литовский 12 с...
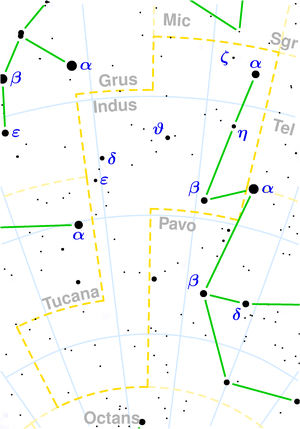
الهندي الاسم اللاتيني Indus المطلع المستقيم 21 الميل −55 ربعية SQ4 المساحة 294 درجة مربعة. (49th) نجومباير/فلامستيد 16 النجوم ضمن 10.00 فرسخ فلكي (32.62 سنة ضوئية) 1 ألمع نجم The Persian (α Ind [لغات أخرى]) (3.11قدر ظاهري) أجرام مسييه لا يوجد زخّات الشهب لايوجد [1] الكوكباتالحدودية المج...

ヨハン・リス作『パエトンの墜落』(17世紀初め) パエトーン(古希: Φαέθων, Phaëthōn)は、ギリシア神話の登場人物である。長母音を省略してパエトン、ファエトン、フェートンとも表記される。 概説 ガイウス・ユリウス・ヒュギーヌスの『神話集』は太陽神ヘーリオスとオーケアノスの娘クリュメネーの子で、ヘーリアデスと兄弟とするが、オウィディウスの...












![{\displaystyle A\vee B\equiv (\exists n)[(n=0\to A)\wedge (n\neq 0\to B)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2435096ffeb76d171a98c3ff7b6a2da3a9f9b0d)








