Mapa de Karnaugh é um método de simplificação gráfico criado por Edward Veitch (1952) e aperfeiçoado pelo engenheiro de telecomunicações Maurice Karnaugh. Chamamos esse diagrama de mapa, visto este ser um mapeamento biunívoco a partir de uma tabela verdade da função que está a ser analisada. Ele é utilizado para simplificar uma equação lógica ou para converter uma tabela verdade no seu circuito lógico correspondente.^[1]

O método de leitura por "mapa de Karnaugh" é considerado mais simples que a "álgebra booleana", pois elimina o problema de erro nas simplificações. Porém quando utilizado mais de 6 entradas, esse método se torna complicado, pois fica difícil identificar as células adjacentes no mapa. Para esse caso são utilizados soluções algorítmicas computacionais.^[1]

Utiliza-se a seguinte tabela-verdade para montar o mapa de Karnaugh, onde A e B são as entradas e F a saída:

     A B    F
 0.  0 0   S0=1
 1.  0 1   S1=0
 2.  1 0   S2=1
 3.  1 1   S3=1

Quando utilizada duas variáveis, o mapa de Karnaugh apresenta a seguinte configuração. Onde cada espaço será completado com seu nível lógico equivalente.Como já possuímos as saídas da tabela verdade do exemplo, colocaremos as mesmas no mapa de Karnaugh.

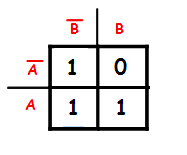
Com o mapa já construído, deve-se diferenciar os minitermos, ou seja, considerar somente os campos que possuem 1 como solução final. Eles devem ser agrupados em pares, para isso ocorrer os elementos tem que estar lado-a-lado, pode ser tanto na horizontal como na vertical. Separando em pares, obtêm-se:

Os campos selecionados com a cor azul, estão respectivamente na coluna B(negado). Já os campos selecionados com a cor laranja estão na linha A. Formando assim a expressão simplificada: ${\displaystyle {\overline {B}}+A}$

Utiliza-se a seguinte tabela-verdade para esse exemplo, onde A, B e C são entradas e S a saída:

Selecionando os elementos que estão no nível lógico 1, obtemos a seguinte expressão ${\displaystyle S={\overline {A}}.{\overline {B}}.C+{\overline {A}}.B.C+A.{\overline {B}}.{\overline {C}}+A.{\overline {B}}.C+A.B.{\overline {C,}}}$ a qual é possível simplificar pelo mapa de Karnaugh. Quando utilizarmos três variáveis, o mapa apresenta a configuração apresentada abaixo, completando o mapa com as saídas obtidas da tabela verdade, teremos:

Os campos selecionados com a cor amarela estão na coluna da variável C e linha da variável A(negado). Já os elementos com a cor verde, pertencem à coluna da variável C(negado) e linha da variável A. Os elementos circundados de rosa, são da coluna B(negado) e C. Sendo assim, a simplificação da equação é:

${\displaystyle {\overline {A}}.C+A.{\overline {C}}+{\overline {B}}.C}$

Primeiramente vamos pegar os resultados da tabela verdade para continuarmos o exemplo.

     A B C D    F
  0. 0 0 1 0  S0 = 1
  1. 0 1 0 1  S1 = 1
  2. 0 1 1 1  S2 = 1
  3. 1 0 1 0  S3 = 1
  4. 1 0 1 1  S4 = 1
 

Onde : Ḡ = (~G)
 Ficando com a expressão: F = (~A)BD + A(~B)C + (~B)C(~D)

Nesta tabela pode-se observar os valores das variáveis "A", "B", "C", "D" e o resultado final("F") da expressão. Agora que já possuímos as saídas da tabela verdade, colocaremos as mesmas no mapa de Karnaugh. A tabela mostrada acima possui 16 saídas, assim, o arranjo mais conveniente, é uma matriz 4x4, desta forma.

Com o mapa já construído, o que devemos fazer agora é diferenciar os mintermos dos maxtermos, ou seja, considerar somente os locais que possuem 1 como solução final.

Cada “símbolo” sendo eles A, B, C, D ou suas respectivas negações, correspondem a 8 campos cada. A visão pelo mapa depende desses campos, sendo assim, as maiores aglomerações de valores 1 serão a solução final da expressão. Essas aglomerações devem ser quadrados ou retângulos e também devem conter quantidades baseadas em potências de 2, ou seja, 2, 4 ou 8.

Exemplos

As maiores quantidades de locais com valor 1 que conseguimos verificar são:

Os campos selecionados com a cor azul, estão respectivamente na coluna da variável C e na linha das variáveis B(negado) e A(negado). A cor roxa seleciona todos os campos da variável D. A cor verde seleciona alguns campo na linha da variável A e coluna da negação da variável C(negado). Sendo assim, a expressão simplificada para este exemplo é a seguinte: ${\displaystyle C.{\overline {B}}.{\overline {A}}+D+A.{\overline {C}}}$

O mapa de Karnaugh utilizando 5 variáveis é representado por 25 soluções, ou seja, 32 saídas da função. Para esta representação, utilizamos duas matrizes 4x4. Veremos abaixo um exemplo para melhor entendimento e utilização desse método.

     A B C D E   F
  0. 0 0 0 0 0  S0 = 0
  1. 0 0 0 0 1  S1 = 0
  2. 0 0 0 1 0  S2 = 0
  3. 0 0 0 1 1  S3 = 0
  4. 0 0 1 0 0  S4 = 0
  5. 0 0 1 0 1  S5 = 1
  6. 0 0 1 1 0  S6 = 0
  7. 0 0 1 1 1  S7 = 0
  8. 0 1 0 0 0  S8 = 1
  9. 0 1 0 0 1  S9 = 1
 10. 0 1 0 1 0 S10 = 1
 11. 0 1 0 1 1 S11 = 0
 12. 0 1 1 0 0 S12 = 0
 13. 0 1 1 0 1 S13 = 1
 14. 0 1 1 1 0 S14 = 1
 15. 0 1 1 1 1 S15 = 0
 16. 1 0 0 0 0 S16 = 0
 17. 1 0 0 0 1 S17 = 0
 18. 1 0 0 1 0 S18 = 0
 19. 1 0 0 1 1 S19 = 0
 20. 1 0 1 0 0 S20 = 0
 21. 1 0 1 0 1 S21 = 1
 22. 1 0 1 1 0 S22 = 1
 23. 1 0 1 1 1 S23 = 0
 24. 1 1 0 0 0 S24 = 0
 25. 1 1 0 0 1 S25 = 0
 26. 1 1 0 1 0 S26 = 0
 27. 1 1 0 1 1 S27 = 0
 28. 1 1 1 0 0 S28 = 1
 29. 1 1 1 0 1 S29 = 1
 30. 1 1 1 1 0 S30 = 1
 31. 1 1 1 1 1 S31 = 1

Nesta tabela podemos observar os valores das variáveis “A”, “B”, “C”, “D”, “E” e o resultado final(F) da expressão.

Agora que já possuímos as saídas da tabela verdade, colocaremos as mesmas no mapa de Karnaugh da seguinte forma:

Com o mapa já construído, o que devemos fazer agora é diferenciar os mintermos dos maxtermos, ou seja, considerar somente os locais que possuem 1 como solução final.

Cada “símbolo”, sendo eles A, B, C, D, E ou suas respectivas negações, correspondem a 16 campos cada. A visão pelo mapa depende desses campos, sendo assim, as maiores aglomerações de valores 1 serão a solução final da expressão. Essas aglomerações devem ser quadrados ou retângulos e também contendo quantidades baseadas em potências de 2, ou seja, 2, 4, 8 ou 16. Solução do exemplo Os campos selecionados com a cor amarela estão respectivamente no lado correspondente à variável A(negado), pertencendo às linhas das variáveis B e C(negado) e na coluna da variável D(negado).

A cor roxa seleciona campos que pertencem ao lado correspondente á variável A(negado), nas colunas das variáveis D e E(negado) e também na linha da variável B. A cor verde seleciona campos tanto em A(negado) quanto A, pertence a linha da variável C e as colunas das variáveis D(negado) e E. A cor azul seleciona os campos no lado correspondente á variável A, nas linhas das variáveis C e B.

A cor laranja seleciona campos que pertencem ao lado correspondente á variável A, nas colunas das variáveis D e E(negado) e também na linha da variável C. Sendo assim, a expressão final para este exemplo é a seguinte: ${\displaystyle {\overline {A}}.B.{\overline {C}}.{\overline {D}}+{\overline {A}}.B.D.{\overline {E}}+C.{\overline {D}}.E+A.B.C+A.C.D.{\overline {E}}}$

Referências

• «Karma». Software acadêmico para visualização e solução de mapas de Karnaugh de 2 até 8 variáveis, além de outras ferramentas relacionadas a síntese lógica. LogiCS, UFRGS. 
• «Calculadora de Veitch Karnaugh» 
• Algoritmo de Quine-McCluskey