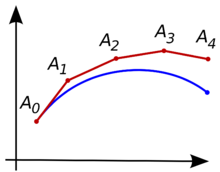
Método de Euler
|
Read other articles:

Jang Hyun-soo Swedia mengalahkan Korea Selatan di Piala Dunia 2018Informasi pribadiTanggal lahir 28 September 1991 (umur 32)Tempat lahir Korea SelatanPosisi bermain BekKarier senior*Tahun Tim Tampil (Gol)2012-2013 FC Tokyo * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Jang Hyun-soo (lahir 28 September 1991) adalah pemain sepak bola asal Korea Selatan. Karier Jang Hyun-soo pernah bermain untuk FC Tokyo. Pranala luar (Jepang) Profil dan statistik di situs web resmi...

Teatro del Mediterraneoparte della seconda guerra mondialeIn verde i territori controllati dalla marina italiana, in rosso i territori controllati dagli alleati nell'estate del 1942.Data10 giugno 1940 - 2 maggio 1945 LuogoBacino del Mar Mediterraneo, comprese l'Italia, la Grecia e le isole dell'Egeo, le coste del Nordafrica dal Marocco all'Egitto, Malta, Gibilterra, la costa meridionale della Francia EsitoVittoria Alleata Schieramenti Germania Italia (1940-1943) Albania Bulgar...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Kacamata hitam – berita · surat kabar · buku · cendekiawan · JSTOR Gambaran kacamata hitam Seorang wanita menggunakan kacamata hitam Kacamata hitam (Inggris: Sunglasses) salah satu kacamata pelindungan u...

Chronologie de la France ◄◄ 1830 1831 1832 1833 1834 1835 1836 1837 1838 ►► Chronologies Honoré Daumier, « Le Ventre législatif », aspects des bancs ministériels de la chambre improstituée de 1834. Lithographie publiée dans L'Association mensuelle en janvier 1834.Données clés 1831 1832 1833 1834 1835 1836 1837Décennies :1800 1810 1820 1830 1840 1850 1860Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier &#...

لمعانٍ أخرى، طالع مكسيكو (توضيح). مكسيكو الإحداثيات 43°27′21″N 76°12′20″W / 43.455833333333°N 76.205555555556°W / 43.455833333333; -76.205555555556 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة أوسويغو خصائص جغرافية المساحة 121703541 متر مربع ار...

Pour les articles homonymes, voir Lambert et Christophe Lambert (homonymie). Christophe LambertBiographieNaissance 10 octobre 1964Fontenay-sous-BoisDécès 13 mai 2016 (à 51 ans)15e arrondissement de MarseilleNom de naissance Christophe Jean-Pierre LambertNationalité françaiseActivités Écrivain, conseiller ou conseillère en communication, publicitaire, producteur de cinémaConjoint Marie Sara (de 2007 à 2016)Autres informationsParti politique Union pour un mouvement populairemodi...

إدواردو لويس معلومات شخصية الميلاد 6 ديسمبر 1955 (العمر 68 سنة)لوريس الطول 1.80 م (5 قدم 11 بوصة) مركز اللعب مدافع الجنسية البرتغال مسيرة الشباب سنوات فريق 1971–1972 Olivais Sul 1972–1974 بنفيكا المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1974–1975 ماريتيمو 0 (0) 1975–1976 بنفيكا 3 (0) 1976–1982 ماريتي...

Nomagliocomune Nomaglio – VedutaFontana in pietra LocalizzazioneStato Italia Regione Piemonte Città metropolitana Torino AmministrazioneSindacoEllade Giacinta Peller (lista civica) dall'8-6-2009 (3º mandato dal 27-5-2019) TerritorioCoordinate45°32′10.18″N 7°51′37.14″E / 45.53616°N 7.860317°E45.53616; 7.860317 (Nomaglio)Coordinate: 45°32′10.18″N 7°51′37.14″E / 45.53616°N 7.860317°E45.53616; 7.860317 ...

Untuk kegunaan lain, lihat A.U.C. dan AUC. Koin antoninianus dari Pacatianus, pesaing pada zaman kaisar Romawi Filipus si Arab pada tahun 248 M. Memuat tulisan ROMAE AETER[NAE] AN[NO] MIL[LESIMO] ET PRIMO, Untuk Roma yang kekal, pada tahun ke-1001. Ab urbe condita (A.U.C.), artinya adalah setelah kota (Roma) didirikan, yaitu pada tanggal 21 April tahun 753 SM menurut tulisan Livius. Ini dipakai oleh orang Romawi untuk menulis tahun. Pada renaissance digunakan dalam naskah untuk menunjukan sis...

Subway station in Philadelphia, Pennsylvania Not to be confused with 36th Street Portal. 36th Street36th Street station platformGeneral informationLocation36th and Sansom StreetsPhiladelphia, Pennsylvania, U.S.Coordinates39°57′14″N 75°11′41″W / 39.953890°N 75.194630°W / 39.953890; -75.194630Owned bySEPTAPlatforms2 side platformsTracks2Connections SEPTA City Bus: 21ConstructionStructure typeUndergroundAccessibleNoHistoryOpenedNovember 1955 (1955-11...

Drachenbronn-Birlenbachcomune Drachenbronn-Birlenbach – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Basso Reno ArrondissementWissembourg CantoneWissembourg AmministrazioneSindacoPierre Koepf TerritorioCoordinate48°59′12″N 7°52′16″E / 48.986667°N 7.871111°E48.986667; 7.871111 (Drachenbronn-Birlenbach)Coordinate: 48°59′12″N 7°52′16″E / 48.986667°N 7.871111°E48.986667; 7.871111 (Drachenbronn-Birlenbach)...

馬哈茂德·艾哈迈迪-内贾德محمود احمدینژاد第6任伊朗總統任期2005年8月3日—2013年8月3日副总统帷爾維茲·達烏迪穆罕默德-禮薩·拉希米领袖阿里·哈梅內伊前任穆罕默德·哈塔米继任哈桑·魯哈尼不结盟运动秘书长任期2012年8月30日—2013年8月3日前任穆罕默德·穆尔西继任哈桑·魯哈尼德黑蘭市長任期2003年6月20日—2005年8月3日副职阿里·賽義德盧前任哈桑·馬利克邁達尼�...

Australian politician (1856–1919) The HonourableAlfred DeakinDeakin in 19052nd Prime Minister of AustraliaIn office2 June 1909 – 29 April 1910MonarchEdward VIIGovernor‑GeneralLord DudleyPreceded byAndrew FisherSucceeded byAndrew FisherIn office5 July 1905 – 13 November 1908MonarchEdward VIIGovernors‑GeneralLord NorthcoteLord DudleyPreceded byGeorge ReidSucceeded byAndrew FisherIn office24 September 1903 – 27 April 1904MonarchEdward VIIGover...

LGBT rights in NorwayLocation of Norway (dark green)in Europe (dark grey) – [Legend]StatusLegal since 1972Gender identityTransgender people allowed to change legal sex based on self-determinationMilitaryLGBT people allowed to serve openly.Discrimination protectionsSexual orientation, gender identity/expression, intersex status protections (see below)Family rightsRecognition of relationshipsSame-sex marriage since 2009AdoptionFull adoption rights since 200...

Азербайджанский государственный экономический университет(АГЭУ) Международное название Azerbaijan State Economic University Год основания 19 июня 1930[1] Ректор Адалят Мурадов Студенты 18 400 Расположение Азербайджан, Баку Юридический адрес Баку, ул. Истиглалият 6. Сайт unec.edu.az М�...

Radio station in Brighton, New YorkWZNEBrighton, New YorkBroadcast areaRochester metro areaFrequency94.1 MHz (HD Radio)Branding94-1 The ZoneProgrammingFormatAlternative rockHD2: Indie rockOwnershipOwnerStephens Media Group(Stephens Media Group Rochester, LLC)Sister stationsWFKL, WRMM-FMHistoryFirst air dateApril 11, 1997 (1997-04-11)Former call signsWAQB (1997)Call sign meaningWe're in the ZoNETechnical informationFacility ID6859ClassAERP1,800 wattsHAAT124 metersTransmitter co...
陳家薰个人资料本名陳家薰罗马拼音Chen Chia-Hsun所属国家队 中華臺北出生 (1991-10-15) 1991年10月15日(32歲) 中華民國(臺灣)教育程度正修科技大學母校高雄市立海青高級工商職業學校正修科技大學活跃年代2008年-身高1.85米(6英尺1英寸)体重76公斤(168英磅)配偶莊志涵(2018年结婚)运动国家/地区 中華民國(臺灣)运动田徑项目短跑职业院校校队正修科技大�...

Politics of Sudan Member State of the Arab League Constitution 4 August 2019 Draft Constitutional Declaration Executive Presidency Transitional Sovereignty Council Chairman: Abdel Fattah al-Burhan Deputy Chairman: Malik Agar Prime Minister Osman Hussein (acting) Cabinet Legislature Transitional Legislative Council Judiciary Constitutional Court Supreme Court Chief Justice Nemat Abdullah Khair Court of Cassation Public Court District Courts Town and rural courts Administrative divisions State...

Type D An Avro Type D equipped as a floatplane. This particular aircraft made its first flight on 18 November 1911. Role Experimental aircraftType of aircraft Manufacturer Avro Designer Alliott Verdon Roe First flight 1 April 1911[1] Number built 7 The Avro Type D was an aircraft built in 1911 by the pioneer British aircraft designer A.V. Roe. Roe had previously built and flown several aircraft at Brooklands, most being tractor layout triplanes. The Type D was his first biplane. Desi...

Pskovavia maskapai penerbangan TempatNegaraRusia SejarahPembuatan1944 Lain-lainSitus webLaman resmi Pskovavia merupakan sebuah maskapai penerbangan kargo yang berbasis di Pskov, Rusia. Maskapai ini mengoperasikan penerbangan charter kargo internasional dan domestik. Basis utamanya terletak di Bandar Udara Pskov.[1] Data Kode Kode ICAO: PSW Panggilan: Pskovavia [2] Sejarah Maskapai penerbangan ini diresmikan dan memulai operasinya pada 1944. Sebelumnya maskapai tersebut bernama...