Lei de ação das massas
|
Read other articles:

Arkarua Periode Ediakara Akhir, sekitar 555 jtyl PreЄ Є O S D C P T J K Pg N ↓ Restorasi senimanTaksonomiKerajaanAnimaliaFilumEchinodermataKelasEdrioasteroideaGenusArkarua James G. Gehling, 1987 Tata namaDinamakan berdasarkanArkaroo (en) lbs Arkarua adami adalah hewan penyaring pasif (diperkirakan)[1] yang diketahui dari fosil-fosil dari akhir periode Ediakara. Fosil Arkarua berbentuk cakram dengan pusat yang meninggi. Terdapat ceruk-ceruk radial di sisi-sisinya, beserta...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Malin Kundang dapat mengacu pada beberapa hal berikut: Malin Kundang, cerita rakyat yang berasal dari provinsi Sumatera Barat, Indonesia Malin Kundang (lagu), lagu karya Orkes Gumarang, dengan iringan vokal oleh Juni Amir Malin Kundang (film), film ta...

Platybelodon Periode Miosen, 15–10 jtyl PreЄ Є O S D C P T J K Pg N ↓ Platybelodon grangeri (en) Sebuah gambar ilustrasi dari Platybelodon grangeri.TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoProboscideaFamiliAmebelodontidaeGenusPlatybelodon Borissiak, 1928 Spesies P. danovi Borissiak, 1928 (type) P. grangeri Osborn, 1929 P. loomisi (Barbour, 1929) P. barnumbrowni (Barbour, 1931) lbs Platybelodon (taring senjata datar) adalah genus mamalia herbivor besar yang berkera...

Administrative entry restrictions Visa requirements for New Zealand citizens are administrative entry restrictions by the authorities of other states placed on citizens of New Zealand. As of 2024, New Zealand citizens had visa-free or visa on arrival access to 190 countries and territories, ranking the New Zealand passport 5th in the world according to the Henley Passport Index.[1] Visa requirements map Visa requirements for New Zealand citizens holding ordinary passports ...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (January 2018) (Learn how and when to remove this template message) Seven Generations Education InstituteMottoCulturally enriched quality education for allTypeAboriginal-owned and controlled education institutionEstablished1985 as Rainy Lake Ojibway Education Author...
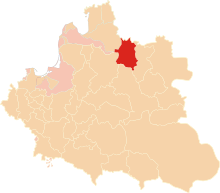
Voivodeship of the Grand Duchy of Lithuania Polotsk VoivodeshipWojewództwo połockiePalatinatus PolocensisVoivodeship of the Grand Duchy of Lithuania, later Polish–Lithuanian Commonwealth1504–1793 Coat of arms Połock Voivodeship in red. Voivodeship's borders did not change since the Union of Lublin.Połock Voivodeship in the Polish–Lithuanian CommonwealthCapitalPołockArea • 21,800 km2 (8,400 sq mi)History • Established 1504• Second Partit...

Conseil régional deBourgogne-Franche-Comté Mandature 2021-2028 Conseil régional de BourgogneConseil régional de Franche-Comté Logo de la région Bourgogne-Franche-ComtéPrésentation Type Conseil régional Création 1er janvier 2016 Lieu Besançon, square Castan Durée du mandat 6 ans Présidence Présidente Marie-Guite Dufay (PS) Élection 4 janvier 2016 Structure Membres 100 conseillers régionaux Composition actuelle.Données clés Groupes politiques Majorité (57) Notre Région...

1999 video game 1999 video gameTeam Fortress ClassicDeveloper(s)ValvePublisher(s)Sierra StudiosValve (digital)Designer(s)John CookRobin WalkerEngineGoldSrcPlatform(s)Microsoft Windows, OS X, LinuxRelease April 7, 1999 Windows April 7, 1999 OS X, Linux August 12, 2013 Genre(s)First-person shooterMode(s)Multiplayer Team Fortress Classic is a first-person shooter game developed by Valve and published by Sierra Studios. It was originally released in April 1999 for Windows, and is based on Team Fo...

Torneo Internacional de Ajedrez Ciudad de LinaresSport Scacchi Paese Spagna LuogoLinares Cadenzaannuale StoriaFondazione1978 Soppressione2010 Numero edizioni27 Ultimo vincitoreVeselin Topalov Record vittorieGarri Kasparov (9) Modifica dati su Wikidata · Manuale L'annuale torneo di scacchi di Linares derivava il nome dalla città spagnola di Linares in Andalusia, che lo ospitava. La sua importanza era tale che venne talvolta descritto come la Wimbledon degli scacchi. Indice 1 Storia...

2000 film by Tarsem Singh This article is about the 2000 film. For the 2016 film, see Cell (film). The CellTheatrical release posterDirected byTarsem SinghWritten byMark ProtosevichProduced by Julio Caro Eric McLeod Starring Jennifer Lopez Vince Vaughn Vincent D'Onofrio Marianne Jean-Baptiste Jake Weber Dylan Baker CinematographyPaul LauferEdited by Paul Rubell Robert Duffy[1] Music byHoward ShoreProductioncompanyRadicalMediaDistributed by New Line Cinema (United States) Kinowelt Film...

French politician Émile BollaertHigh Commissioner of IndochinaIn office5 March 1947 – 19 October 1948 Personal detailsBorn(1890-11-13)13 November 1890Dunkirk, FranceDied18 May 1978(1978-05-18) (aged 87)Paris, France Émile Bollaert (13 November 1890 – 18 May 1978)[1] was French High Commissioner of Indochina from 5 March 1947 to 19 October 1948.[2][1][3] He was one of the senators elected by the National Assembly who held office during the Fr...

2016年美國總統選舉 ← 2012 2016年11月8日 2020 → 538個選舉人團席位獲勝需270票民意調查投票率55.7%[1][2] ▲ 0.8 % 获提名人 唐納·川普 希拉莉·克林頓 政党 共和黨 民主党 家鄉州 紐約州 紐約州 竞选搭档 迈克·彭斯 蒂姆·凱恩 选举人票 304[3][4][註 1] 227[5] 胜出州/省 30 + 緬-2 20 + DC 民選得票 62,984,828[6] 65,853,514[6]...

Ini adalah nama Melayu; nama Saibi merupakan patronimik, bukan nama keluarga, dan tokoh ini dipanggil menggunakan nama depannya, Salina. Salina SaibiSaibi diwawancarai pada 2014.Lahir10 Januari 1982 (umur 42)Kuala Lumpur, MalaysiaPendidikanSijil Pelajaran Malaysia (SPM)PekerjaanPemeran, modelTahun aktif2001–kiniSuami/istriAzmir Osman (m. 2007)Anak2Orang tuaSaibi Kuntom Salina Saibi (lahir 10 Januari 1982) adalah seorang pemeran dan peraga busana Mala...

Mountain pass in the Hidaka Mountains, Hokkaidō, Japan Karikachi Pass狩勝峠Elevation644 m (2,113 ft)[1]Traversed byJapan National Route 38LocationJapanRangeHidaka MountainsCoordinates43°8′9.6″N 142°45′53.9″E / 43.136000°N 142.764972°E / 43.136000; 142.764972Topo mapGeographical Survey Institute25000:1 狩勝峠25000:1 落合50000:1 夕張岳 Karikachi Pass (狩勝峠, Karikachi-tōge) is a mountain pass at the north end of the Hidaka Mountains o...

2012 German Grand Prix Race 10 of 20 in the 2012 Formula One World Championship← Previous raceNext race → The HockenheimringRace detailsDate 22 July 2012Official name Formula 1 Grosser Preis Santander von Deutschland 2012[1]Location Hockenheimring, Hockenheim, GermanyCourse Permanent racing facilityCourse length 4.574 km (2.842 miles)Distance 67 laps, 306.458 km (190.424 miles)Weather Fine and Dry[2] Air Temp 22 °C (72 °F)[2] Track T...

The Honourable何俊賢Steven Ho Chun-yinBBS JP 議員何俊賢(攝於2023年) 香港立法會議員现任就任日期2012年10月1日前任黃容根选区漁農界 个人资料性别男出生 (1979-11-30) 1979年11月30日(44歲) 英屬香港国籍 中华人民共和国(香港)政党 民主建港協進聯盟职业香港立法會議員 何俊賢,BBS,JP(英語:Steven Ho Chun-yin,1979年11月30日—)[1],綽號高佬賢[2],香港漁民團體聯�...
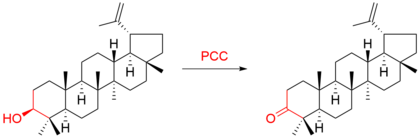
Pyridinium chlorochromate Ball-and-stick model of the pyridinium cation Ball-and-stick model of the chlorochromate anion Names IUPAC name Pyridinium chlorochromate Other names PCC; Corey-Suggs reagent Identifiers CAS Number 26299-14-9 Y 3D model (JSmol) Interactive image ChEBI CHEBI:176795 ChemSpider 10608386 Y ECHA InfoCard 100.043.253 EC Number 247-595-5 PubChem CID 129695875 UNII DTV5HU1N27 Y CompTox Dashboard (EPA) DTXSID40893953 InChI InChI=1S/C5H5N.ClH.Cr.3O/c1-2-4-6-5-3...

For other uses, see Basra (disambiguation). Basrah redirects here. For the village in eastern Yemen, see Basrah, Yemen. Not to be confused with Bosra, Busra al-Harir, or Bozrah. Metropolis in IraqBasra ٱلْبَصْرَةBasrahMetropolisNickname: Venice of the East[1]BasraLocation of Basra within IraqShow map of IraqBasraBasra (Near East)Show map of Near EastCoordinates: 30°30′54″N 47°48′36″E / 30.51500°N 47.81000°E / 30.51500; 47.81000Country...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cecilia Pantoja – news · newspapers · books · scholar · JSTOR (July 2023) (Learn how and when to remove thi...

This article is about the historical Croatian political party. For other uses, see Croatian Party of Rights (disambiguation). Political party in Croatia Party of Rights Stranka pravaLeaderAnte StarčevićFounderAnte StarčevićEugen KvaternikFounded26 June 1861 (1861-06-26)Dissolved6 January 1929 (1929-01-06)HeadquartersZagrebNewspaperHrvatsko pravoIdeologyCroatian nationalismCroatian irredentism[1]National conservatismMonarchism[2][3]...
![{\displaystyle K={\frac {[S]^{\sigma }[T]^{\tau }\dots }{[A]^{\alpha }[B]^{\beta }\dots }}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b78c2a85b73880c965b62ed22ef56d8b08fa5084)
![{\displaystyle r_{f}=k_{f}[A][B]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e942fd6e6cc804f55daa31f5632cd64ac39ebaa3)
