Lei de Vegard
A Lei de Vegard pode ser usada para microscopia eletrônica de varredura de elétrons, juntamente com técnicas de espectroscopia de energia dispersa de raios-X [1]., além de ser capaz de calcular os parâmetros de rede correspondentes a nanofios individuais contendo poços multiquânticos.[2]. Desde amostras caracterizadas por XRD usando de alta resolução, como as sondas de raios X baseadas em Síncrotron chegando à nanoescala, além de ser uma poderosa ferramenta para o estudo de nanoestruturas semicondutoras e nanodispositivos, sem destruir o material.[3]
As abordagens de Lars Vegard e obtenção da Lei
Tendo início no decorrer da primeira guerra mundial, as investigações dos cristalitos tiveram como base o cloreto de potássio (KCl) do qual é um tipo de sal o que acaba facilitando a energização das ligações, e o cloreto de bromo (KBr), do qual é um tipo de halogênio não-metal, ou seja, suas moléculas serão neutras, com intuito de ter ligações a base de Forças de Van der Walls[1], assim Vergard fez o uso inicial da metodologia de ionização de Bragg-Gray, que nada mais é do que a relação a uma dosagem de radiação num volume de cavidade de material à outra dosagem que existiria em um meio circundante na ausência do volume da cavidade, porém, apresentando dificuldades na obtenção de pontos máximos de reflexão nítidos e não montados dos cristalitos. [4]. Ainda seguindo os mesmos elementos, todavia mudando para metodologia de [Debye-Scherer][5], onde temos a observação do padrão de difração formado quando se faz incidir um feixe de raios X monocromáticos sobre uma amostra pulverizada, cujas orientações relativas são aleatórias. Satisfazendo a lei de Bragg, onde o efeito dessa aleatoriedade é que os feixes de raios X difratados[4].
Vergard então elabora através dessa metodologia, e com final da primeira grande guerra, uma lei empírica, cujo parâmetro de rede de uma solução sólida de constituintes (α_SS) é na verdade a aproximação da média ponderada[6] dos parâmetros de rede dos dois constituintes na mesma temperatura varia linearmente com a proporção da mistura, como vista a seguir:


Assim teremos:

Antes de se obter a mistura, os componentes A e B assumem sua forma, ou seja, sua estruturar cristalina se mantem pura. Assim, para se obter estimativas aproximadas de dados experimentais, ela se torna uma ferramenta interessante, quando alguns desde dados não estão bem detalhados no sistema a ser desejado na pesquisa de um determinado cristal. O, porém é que a lei não é totalmente precisa, pois desvios do comportamento linear ocorrem.[7]
Aplicações da Lei de Vegard
Suas aplicações de modo geral estão relacionadas as melhorias na resolução espacial de difratogramas e a absorção de raios-X perto de ordem de longo e curto alcance da estrutura do material analisado, das quais baseam-se no Síncrotron chegando à nanoescala e constituem, atualmente, uma poderosa ferramenta para o estudo de nanoestruturas semicondutoras e nanodispositivos que proporcionam alta sensibilidade sem destruir o material. Algumas técnicas contendo poços multiquânticos não polares, a análise ultrassensível, sem causar danos ao material utilizado nas nanoestruturas elementares, faz com que seja capaz de determinar a concentração de suas heterogeneidades.[2] Essas estruturas não homogêneas são baseadas em nanofios, como poços quânticos (QWs), são reconhecidas como suporte ideal para dispositivos optoeletrônicas altamente eficientes como diodos emissores de luz, diodos laser e fotodiodos.[3]
As medições de nano difratoras de raio X podem abordar a fase do cristal e os parâmetros de rede de diferentes regiões individuais. A curta distância que separa o CCD da amostra [Figura 1] permitiu que três picos de difração fossem medidos simultaneamente, cuja identificação desses picos é realizada com os programas Fit2D e PYMCA, apontou que eles correspondem a (104), (210) e (211) reflexões de Wurtzita GaN não tensionada. Uma dessas reflexões de Bragg é mostrada em escala logarítmica em Figura 1a. Nem reflexões adicionais nem assimetrias são observadas, apenas picos de difração correspondentes a reflexões GaN não tensionadas foram detectados estudando o sinal de DRX. Uma vez que a concentração de In foi medida por XRF, a lei de Vergard pode ser usada para calcular os parâmetros de rede correspondentes a 'InGaN QWs não tensionados e, a partir desses, as posições angulares dos reflexos de (210) e (211) Bragg de InGaN. Para uma concentração de 7,6% em In, os picos de XRD devem aparecer em 2θ 210= 24,262 ° e 2θ 211 = 24,757 °, que são representados como linhas tracejadas em Figura 4b.[2]
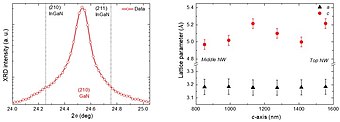
Figura 1 (adaptado[2]):(a) Pico de difração de XRD medido na região do meio de uma nanosonda individual e plotado em escala logarítmica. As linhas tracejadas indicam as posições dos picos de XRD correspondentes a GaN não tensionado (210) e InGaN (210) e (211) com uma concentração média de In de x = 0,076. (b) Evolução dos parâmetros da rede Wurtzita a e c ao longo do eixo z da nanosonda, partindo do meio da nanosonda em direção ao seu topo.[2]
Referências
- ↑ a b Vergard, L. (1921). "Die konstitution der mischkristalle und die raumfüllung der atome" (Tese). Zeitschrift für Physik. pp. 5: 17–26.
- ↑ a b c d e Secco E., Mengistu H.T., Ruíz J.S., Criado G.M., Cristóbal A.G., Cantarero A., Foltynski B, Behmenburg H., Giesen C., Heuken M. and Garro N., (2019). "Elemental Distribution and Structural Characterization of GaN/InGaN Core-Shell Single Nanowires by Hard X-ray Synchrotron Nanoprobes" (Tese). Paterna (València) e Madrid - Spain, Grenoble - France, Herzogenrath - Germany: Institut de Ciència dels Materials (ICMUV), Universitat de València, Paterna (València), Spain; ESRF—The European Synchrotron, Grenoble, France; Instituto de Ciencia de Materiales de Madrid (ICMM), Consejo Superior de Investigaciones Científicas (CSIC), Madrid, Spain; Institut de Ciència Maolecular (ICMOL), Universitat de València, Paterna (València), Spain; AIXTRON SE, Dornkaulstrasse, Herzogenrath,. 12 páginas.
- ↑ a b Ceponis T, Badokas K, Deveikis L, Pavlov J, Rumbauskas V, Kovalevskij V, Stanionyte S, Tamulaitis G and Gaubas E. (2019). “Evolution of Scintillation and Electrical Characteristics of AlGaN Double-Response Sensors During Proton Irradiation” (Tese). Sauletekio, Vilnius - Lithuania: Institute of Photonics and Nanotechnology, Vilnius University, Sauletekio and Centre for Physical Sciences and Technology. 11 páginas.
- ↑ a b Attix, F.H (1986). “Introduction to Radiological Physics and Radiation Dosimetry” (Tese). New York: John Wiley & Sons. pp. .
- ↑ Martins, D.S (2007). “Implementação de um método de análise de imagens para integração da intensidade de raios x espalhados em uma câmera de debye-scherrer” (Tese). Santa Maria - RS: Universidade Federal de Santa Maria, Curso de Física Santa Maria. pp. .
- ↑ Denton,Ashcroft, A.R,N.W (1991). "Vegard's law" (Tese). Phys. Rev. A. 6 páginas.
- ↑ King, H.W (1966). "Quantitative size-factors for metallic solid solutions" (Tese). Journal of Materials Science. pp. 79–90.