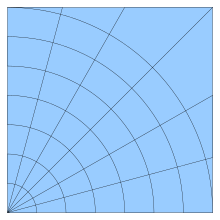
Grade cartesiana

Exemplo de uma grade cartesiana.
Exemplo de uma grade regular.
Exemplo de uma grade retilinear.
Exemplo de uma grade curvilinear.

Uma grade regular é uma tesselação de um Espaço euclidiano de n dimensões criado por paralelepípedos.[1] Grades desse tipo aparecem em papéis milimetrados e podem ser usados em Método dos elementos finitos, assim como em Método dos volumes finitos e em Método das diferenças finitas. Como as derivadas de campo são expressas convenientemente como diferenças finitas,[2] grades estruturadas aparecem muito em métodos de diferença finita. Grades desestruturadas oferecem mais flexibilidade que grades estruturadas e, por isso, são mais úteis em métodos de volume e elementos finitos.

Cada célula na grade pode ser endereçada pelo índice em duas (i,j) ou três (i,j,k) dimensões, e cada vértice tem coordenadas em 2D ou em 3D para algum número real dx, dy e dz representando o espaço da grade.

Grades relacionadas

Uma Grade cartesiana é um caso especial onde os elementos são quadrados unitários ou cubos unitários e os vértices são pontos inteiros.

Uma Grade retilinear é uma tesselação de retângulos ou paralelepípedos que não são, em geral, todos congruentes. As células ainda podem ser indexadas por inteiros, como na grade cartesiana, mas o mapeamento de índices para coordenadas de vértices é menos uniforme que uma grade regular.

Uma Grade curvilinear ou Grade estruturada é uma grade que possui a mesma estrutura de uma grade regular, onde as células são quadriláteras ou cúbicas, ao invés de relangulos e paralelepípedos retangulares.

Ver também

Notas

  • Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Regular Grid».

Referências

  1. ↑ Uznanski, Dan. «Grid.». From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Consultado em 25 de março de 2012 
  2. ↑ J.F. Thompson, B. K . Soni & N.P. Weatherill (1998). Handbook of Grid Generation. [S.l.]: CRC-Press. ISBN 978-0-8493-2687-5 

Read other articles:

Damblain

Peta infrastruktur dan tata guna lahan di Komune Damblain.  = Kawasan perkotaan  = Lahan subur  = Padang rumput  = Lahan pertanaman campuran  = Hutan  = Vegetasi perdu  = Lahan basah  = Anak sungaiDamblain merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE lbsKomune di departemen Vosges Les Ableuvenettes Ahéville Aingeville Ainvelle Allarmont Ambacourt Ameuv...

 

Cape Bon

Cape BonPeninsulaCape Bon from space (false color)Location in TunisiaKoordinat: 36°45′N 10°45′E / 36.750°N 10.750°E / 36.750; 10.750Koordinat: 36°45′N 10°45′E / 36.750°N 10.750°E / 36.750; 10.750LokasiNabeul Governorate, Tunisia Tanjung Bon (Tanjung Baik), juga dikenal sebagai Res et-Teib (Arab: الرأس الطيبcode: ar is deprecated ), [1] Semenanjung Shrīk, atau Watan el Kibli, [2] adalah sebuah semenanjun...

 

Gare de Marseille Saint-Charles

Tangga utama stasiun Saint-Charles. Le Grand Escalier dan boulevard d'Athènes di Marseille, dilihat dari stasiun Saint-Charles. Saint Charles merupakan stasiun kereta api utama Marseille. Stasiun ini merupakan ujung terminal dan dibuka pada 8 Januari 1848, setelah dibangun untuk PLM di atas tanah Pemakaman Saint Charles. Letaknya di puncak sebuah bukit kecil dan terhubung dengan kota oleh sebuah tangga. Stasiun ini pernah berperan dalam perjalanan menuju Afrika dan Timur Tengah sebelum muncu...

Farmakologi

Farmakologi adalah Istilah yang berasal dari bahasa Yunani yaitu Farmakos yang memiliki arti obat dan Logos yang artinya ilmu.[1] Jadi secara harfiah, farmakologi dapat ditafsirkan sebagai suatu ilmu yang mempelajari obat dan cara kerjanya pada sistem biologis. Terutama tentang obat yang berkaitan dengan respons bagian-bagian tubuh terhadap sifat obat, pengaruh sifat fisika-kimiawinya terhadap tubuh, kegunaan obat bagi kesembuhan dan nasib yang dialami obat dalam tubuh.[2] Ar...

 

Cogito, ergo sum

Philosophical statement made by René Descartes I think, therefore I am redirects here. For the R. Dean Taylor album, see I Think, Therefore I Am. For the Billie Eilish song referencing Descartes' principle, see Therefore I Am (song). Part of a series onRené Descartes Philosophy Cartesianism Rationalism Foundationalism Mechanism Doubt and certainty Dream argument Cogito, ergo sum Evil demon Trademark argument Causal adequacy principle Mind–body dichotomy Analytic geometry Coordinate system...

 

Daftar penumpang RMS Titanic

Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Daftar penumpang RMS Titanic. Contoh paragraf pembuka Daftar penumpang RMS Titanic adalah .... (Juni 2020) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Daftar penumpang Kelas satu Nama Allen, Miss Elizabeth Walton Allison, Mr. Hudson Joshua Creighton Mr. George Swane Miss Amelia Mary Mildred Brown Alliso...

Золотой век Грузии

История Грузииსაქართველოს ისტორია Доисторическая Грузия Шулавери-шомутепинская культураКуро-араксская культураТриалетская культураКолхидская культураКобанская культураДиаухиМушки Древняя история КолхидаАриан-КартлиИберийское царство ФарнавазидыГруз�...

 

Zapping (film)

1999 Spanish filmZappingFilm posterDirected byJuan Manuel Chumilla CarbajosaWritten byJuan Manuel Chumilla CarbajosaProduced byFrancisco RamosStarringAlberto San JuanNatalia DicentaPaz VegaEduard FernándezCinematographyTeo DelgadoEdited byÁngel Hernández ZoidoMusic byMiguel FrancoAlejandro IbáñezProductioncompanyAurum ProduccionesDistributed byAurumRelease dates June 1999 (1999-06) (Málaga) 6 August 1999 (1999-08-06) (Spain) CountrySpainLanguageSpanish ...

 

Fan

Disambiguazione – Se stai cercando altri significati, vedi Fan (disambigua). Questa voce o sezione sull'argomento musica non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: linguaggio poco enciclopedico per un termine d'uso pluridecennale, rischio di ricerche originali Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. I fan in un recital a Buenos...

Australian Alps National Parks and Reserves

This article is about the group of heritage listed protected areas. For the general mountain range and bioregion, see Australian Alps. Protected area in AustraliaAustralian Alps National Parks and ReservesAustraliaThe Australian Alps viewed from Snowy River Road, near Suggan Buggan, Victoria.Map of the region shaded as listed on the National Heritage List.Australian Alps National Parks and ReservesNearest town or cityCanberraCoordinates37°S 148°E / 37°S 148°E / -37...

 

Generale d'armata

Disambiguazione – Se stai cercando altri significati, vedi Generale d'armata (disambigua). Generale d'armata è un grado militare utilizzato in molte forze armate mondiali, cui è investito un ufficiale che nominalmente comanda un'armata. A causa della riduzione di organico delle forze armate mondiali, tale grado è oggi raramente usato. Nei paesi socialisti dell'Europa orientale il grado di generale d'armata era sinonimo di generale dell'Esercito. Dopo la fine del blocco sovietico gli...

 

Dick Radatz

American baseball player (1937-2005) Baseball player Dick RadatzRelief PitcherBorn: (1937-04-02)April 2, 1937Detroit, Michigan, U.S.Died: March 16, 2005(2005-03-16) (aged 67)Easton, Massachusetts, U.S.Batted: RightThrew: RightMLB debutApril 10, 1962, for the Boston Red SoxLast MLB appearanceAugust 15, 1969, for the Montreal ExposMLB statisticsWin–loss record52–43Earned run average3.13Strikeouts745Saves120 Teams Boston Red Sox (1962–1966) Cleveland Indi...

Calendar Girl (DC Comics)

Fictional supervillain Comics character Calendar GirlCalendar Girl, as she appeared in The New Batman AdventuresPublication informationPublisherDC ComicsFirst appearanceThe New Batman AdventuresCreated byPaul DiniIn-story informationFull namePaige Munroe Calendar Girl is a female supervillain who debuted in The New Batman Adventures episode Mean Seasons. Formerly a supermodel named Paige Munroe, the character developed severe self-esteem issues and body dysmorphic disorder after being fired b...

 

世界政區索引

此條目可能包含不适用或被曲解的引用资料，部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队（军事） 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

 

الهلبوت

تحتاج النصوص المترجمة في هذه المقالة إلى مراجعة لضمان معلوماتها وإسنادها وأسلوبها ومصطلحاتها ووضوحها للقارئ، لأنها تشمل ترجمة اقتراضية أو غير سليمة. فضلاً ساهم في تطوير هذه المقالة بمراجعة النصوص وإعادة صياغتها بما يتناسب مع دليل الأسلوب في ويكيبيديا. This article is about the flatfish...

Snowball (single-board computer)

SnowballSnowball-PCB with NovaThor A9500Common manufacturersST-EricssonDesign firmST-EricssonManufacturerCALAO SystemsTypeSingle-board computerProcessorDual Cortex-A9CoprocessorMali-400 MPDimensionsNano-ITX The Snowball is a Nano-ITX-form factor single-board computer using the NovaThor A9500.[1] The Linux-based mobile operating system Tizen was ported to Snowball in early 2012.[2] The Snowball had a public support site at igloocommunity.org,[3] but since support for th...

 

Arctic exploration

Physical exploration of the Arctic region Main article: Exploration The 10 °C (50 °F) mean isotherm in July line (in red) commonly defines the border of the Arctic region. Arctic exploration is the physical exploration of the Arctic region of the Earth. It refers to the historical period during which mankind has explored the region north of the Arctic Circle. Historical records suggest that humankind have explored the northern extremes since 325 BC, when the ancient Greek sailor Pytheas rea...

 

Campionati Internazionali di Sicilia 1996

Campionati Internazionali di Sicilia 1996Sport Tennis Data23 settembre – 29 settembre Edizione17a SuperficieTerra rossa CampioniSingolare Karim Alami Doppio Andrew Kratzmann / Marcos Ondruska 1995 1997 I Campionati Internazionali di Sicilia 1996 sono stati un torneo di tennis giocato sulla terra rossa. È stata la 17ª edizione dei Campionati Internazionali di Sicilia, che fanno parte della categoria World Series nell'ambito dell'ATP Tour 1996. Si sono giocati a Palermo in Italia, dal 23 al...

Втрати силових структур внаслідок російського вторгнення в Україну (липень — грудень 2021)

Докладніше: Втрати силових структур внаслідок російського вторгнення в Україну У статті наведено список втрат українських військовослужбовців у російсько-українській війні з липня по грудень 2021 року. Зміст 1 Всі списки 2 Список загиблих з 1 липня до 31 грудня 2021 року 2.1 �...

 

Quadripoint

Point where four distinct territories meet Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) A quadripoint is a point on Earth where four distinct political territories meet.[1][2] The territories can be of different types, such as national and provincial. In North America, several such places are commonly known as Four Corners. Several examples exist throughout the world that use ot...