Função quadrática
|
Read other articles:

Erlan QoşanovЕрлан ҚошановQoşanov pada tahun 2023 Ketua Mazhilis ke-10PetahanaMulai menjabat 1 Februari 2022WakilPavel KazantsevBalaim Kesebaeva PendahuluNurlan NigmatulinPenggantiPetahanaKepala Administrasi Kepresidenan KazakhstanMasa jabatan18 September 2019 – 1 Februari 2022PresidenNursultan NazarbayevWakil PertamaMäulen ÄşimbaevDauren Abaev PendahuluKrymbek KusherbayevPenggantiMurat NurtileuKepala Kantor Perdana MenteriMasa jabatan2 Februari 2012 –&#...

Buddha beralih ke halaman ini. Untuk agama, lihat Agama Buddha. Buddha beralih ke halaman ini. Untuk kegunaan lain, lihat Buddha (disambiguasi). Je Tsongkhapa Informasi pribadiDikenal sebagaiPendiri aliran Gelug, penulis banyak karya tentang pemikiran dan praktik Buddha Tibet Je Tsongkhapa Bagian dari seri tentangBuddhisme SejarahPenyebaran Sejarah Garis waktu Sidang Buddhis Jalur Sutra Benua Asia Tenggara Asia Timur Asia Tengah Timur Tengah Dunia Barat Australia Oseania Amerika Eropa Af...

Radio station in Lake Elsinore, CaliforniaKJNI-LPLake Elsinore, CaliforniaFrequency101.7 MHzProgrammingFormatChildren's radioOwnershipOwnerJennifer Smart FoundationHistoryFirst air dateNovember 12, 2014; 9 years ago (2014-11-12)Technical information[1]Licensing authorityFCCFacility ID193349ClassL1ERP100 wattsHAAT−14 meters (−46 ft)Transmitter coordinates33°39′29.20″N 117°15′25.80″W / 33.6581111°N 117.2571667°W / 33.6...

French rule in the Dominican Republic (1795–1809) Saint-Domingue1795–1809 Flag Imperial coat of arms of the First French Empire Map of the Spanish colony of Santo Domingo under French control (1795-1809). To the west of the island, on the other side of the border, is the Empire of Haiti (1804-1806). Although Haiti declared itself free from France, France did not recognize Haiti's independence until 1825 in exchange for 150 million gold francs.StatusColony of FranceCapitalSanto DomingoComm...

Circondario di Unstrut-Hainichcircondario(DE) Unstrut-Hainich-Kreis LocalizzazioneStato Germania Land Turingia DistrettoNon presente AmministrazioneCapoluogoMühlhausen/Thüringen TerritorioCoordinatedel capoluogo51°10′12″N 10°30′00″E / 51.17°N 10.5°E51.17; 10.5 (Circondario di Unstrut-Hainich)Coordinate: 51°10′12″N 10°30′00″E / 51.17°N 10.5°E51.17; 10.5 (Circondario di Unstrut-Hainich) Altitudine196 m s.l.m. Sup...

Security law of Bahrain This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (January 2011) (Learn how and when to remove this template message) This article relies excessively on references to primary s...

British economist (1904–1989) For other people named John Hicks, see John Hicks (disambiguation). Sir John HicksHicks in 1972BornJohn Richard Hicks(1904-04-08)8 April 1904Warwick, England, UKDied20 May 1989(1989-05-20) (aged 85)Blockley, England, UKAcademic careerInstitutionGonville and Caius College, CambridgeLondon School of EconomicsUniversity of ManchesterNuffield College, OxfordSchool ortraditionNeo-Keynesian economicsAlma materBalliol College, OxfordInfluencesLéon Walr...

Harry PotterRupert Grint sebagai Ron Weasley dalam film Harry Potter and the Order of the Phoenix.PemeranRupert GrintAsramaGryffindorInformasiNama lengkapRonald Bilius WeasleyKeluargaArthur Weasley (ayah) Molly Weasley (ibu) Bill Weasley (kakak 1) Charlie Weasley (kakak 2) Percy Weasley (kakak 3) Fred Weasley & George Weasley (kakak kembar) Ginny Weasley (adik)PasanganHermione Granger Ronald Ron Bilius Weasley (lahir pada 1 Maret 1980) merupakan tokoh fiksi Joanne Kathleen Rowling dalam s...

American politician This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this message) Julius GoldzierMember of the U.S. House of Representativesfrom Illinois's 4th districtIn officeMarch 4, 1893 – March 3, 1895Preceded byWalter C. NewberrySucceeded byCharles W. WoodmanChicago Alderman[1]In o...

Jeffrey Kaplan Jeffrey Kaplan, noto anche con lo pseudonimo di Tigole (New Jersey, 4 novembre 1972), è un autore di videogiochi statunitense. Inizia la sua carriera lavorando per Blizzard Entertainment nel Maggio del 2002 come tester nel videogioco Warcraft 3[1]. Successivamente contribuì come world designer (dungeon, raid, quest) nel videogioco World of Warcraft[2] e nelle sue due espansioni, lavorando a stretto contatto con Chris Metzen e Pat Nagle. Nel 2009 Kaplan annunci...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

لمعانٍ أخرى، طالع جو أندرسون (توضيح). جو اندرسون معلومات شخصية الميلاد 26 مارس 1982 (العمر 42 سنة)إنجلترا مواطنة المملكة المتحدة الأب مايلز اندرسون الحياة العملية المدرسة الأم أكاديمية ويبر دوغلاس للفنون الدرامية [لغات أخرى] المهنة ممثل اللغات الإنجل�...
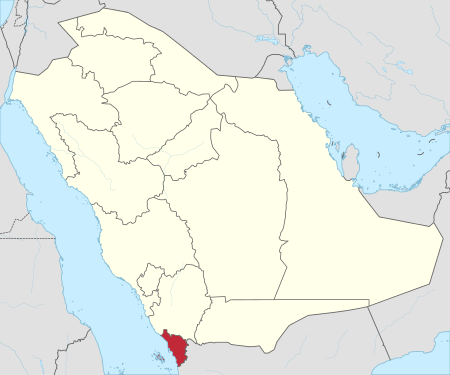
17°08′09.3″N 42°26′43.6″E / 17.135917°N 42.445444°E / 17.135917; 42.445444 مدينة عثر التاريخيةمعلومات عامةنوع المبنى مدينة تاريخيةالمكان محافظة صبيا، منطقة جازانالبلد السعوديةأبرز الأحداثالهدم القرن 11 معلومات أخرىالإحداثيات 19°N 44°E / 19°N 44°E / 19; 44 تعديل - تعديل مصدري - تعدي�...

Private law school in St. Paul, Minnesota William Mitchell College of LawMottoPractical WisdomEstablished1956–2015School typePrivateEndowment$21.5 million[1]DeanEric JanusLocationSt. Paul, Minnesota, United StatesEnrollment930[2]Faculty48 full-time; 300+ adjunctUSNWR ranking134[3]Bar pass rate94.2%[4]Websitehttp://mitchellhamline.edu/ William Mitchell College of Law was a private, independent law school located in St. Paul, Minnesota, United States, from 1956...
Article principal : Aviron aux Jeux olympiques d'été de 2016. Deux sans barreur masculin(M2-)aux Jeux olympiquesd'été de 2016 Généralités Sport Aviron Organisateur(s) CIO Éditions 27e Lieu(x) Rio de Janeiro Date du 6 août 2016 au 11 août 2016 Nations 13 Participants 26 Site(s) Lagoa Rodrigo de Freitas Palmarès Tenant du titre Murray / Bond Vainqueur Murray / Bond Deuxième Brittain / Keeling Troisième Di Costanzo / Abagnale Navigation Londres 2012 Tokyo 2020 modifier L'épreu...

Former Internet Relay Chat client BersircOriginal author(s)Jamie FraterDeveloper(s)Nicholas CopelandStable release2.2.14[1] / 12 August 2005 Written inCOperating systemWindowsTypeIRC clientLicenseLGPLWebsitebersirc.free2code.net Bersirc is a discontinued open-source Internet Relay Chat client for the Microsoft Windows operating system. Linux and Mac OS X versions were in development.[2] Bersirc uses the Claro toolkit, which aims to provide an interface to native windowin...

British music magazine This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: DIY magazine – news · newspapers · books · scholar · JSTOR (February 2014) (Learn how and when to remove this message) DIYEditorSarah JamiesonFormer editorsStephen AckroydCategoriesMusic magazineFrequencyMonthlyPublisherDIY Music Lim...

Questa voce sugli argomenti calciatori francesi e calciatori gabonesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Junior AssoumouNazionalità Gabon Altezza191 cm Peso90 kg Calcio RuoloDifensore Squadra Tours CarrieraSquadre di club1 2013-2014 Rennes 218 (0)2014-2016 Niort 223 (0)2016-2018 Romorantin31 (0)2018 Pau11 (0)2018-2019 Granville20 (1)2019-2020 V...

Bài viết này có nhiều vấn đề. Xin vui lòng giúp đỡ cải thiện nó hoặc thảo luận về những vấn đề này trên trang thảo luận. Bài này dường như được viết theo quan điểm của người hâm mộ. Vui lòng viết lại để bài viết được bách khoa, tập trung trình bày các sự việc đã xảy ra, văn phong khách quan và trung lập, không thiên vị, tâng bốc. (tháng 5 năm 2022) Bài viết này cần thêm chú th�...








































































