Estrutura estelar
|
Read other articles:

List of statements that appear to contradict themselves This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. This list includes well known paradoxes, grouped thematically. The grouping is approximate, as paradoxes may fit into more than one category. This list collects only scenarios that have been called a paradox by at least one source and have their own article in this encyclopedia. Althou...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

House of MouseMiki Tikus dan teman-temannya menjalankan bisnis mereka di House of MousePembuatTony CraigRob GannawayWalt Disney TelevisionPengisi suaraWayne AllwineTony AnselmoRussi TaylorBill FarmerCorey BurtonApril WinchellTress MacNeilleKath SoucieJodi BensonPat CarrollSamuel E. WrightGilbert GottfriedScott WeingerLinda LarkinNegara asal Amerika SerikatJmlh. episode52ProduksiDurasi20 menitRumah produksiThe Walt Disney CompanyRilis asliJaringanABCToon Disney (2002–2009)Disney Channe...

الدوري الهندي للمحترفين 2016–17 تفاصيل الموسم الدوري الهندي للمحترفين النسخة 10 البلد الهند التاريخ بداية:7 يناير 2017 نهاية:30 أبريل 2017 المنظم اتحاد الهند لكرة القدم البطل نادي أيزاول مباريات ملعوبة 90 عدد المشاركين 10 الدوري الهندي للمحترفين 2015–16...

Japanese light novel series Nanana's Buried TreasureFirst light novel volume cover featuring the character Nanana Ryūgajō龍ヶ嬢七々々の埋蔵金GenreSupernatural[1] Light novelWritten byKazuma ŌtorinoIllustrated byAkaringo (vol. 1-7)Non (vol. 8-12)Published byEnterbrainImprintFamitsu BunkoDemographicMaleOriginal runJanuary 30, 2012 – December 28, 2016Volumes12 MangaWritten byKazuma ŌtorinoIllustrated byHitoshi OkudaPublished byEnterbrainMagaz...

Polish automobile factory Fabryka Samochodów MałolitrażowychIndustryAutomotiveFounded1948 (WSM)1971 (FSM)Defunct1992FateAcquiredSuccessorFiat Auto PolandHeadquartersBielsko-Biala, PolandProductsAutomobiles The Fabryka Samochodów Małolitrażowych, commonly known as FSM, was a Polish automobile factory born from an agreement between the FSO and Fiat in the 1970s for the construction of a new model, the Polski Fiat 126p, Polish version of Fiat 126. For the project a new manufacturing plant ...

Cooking school in Hong Kong focusing on Chinese cuisine This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chinese Culinary Institute – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this template message) Chinese Culinary Institutethe entrance of Chinese Culinary Institut...

Member of the Verkhovna Rada (national parliament of Ukraine) People's Deputy of UkraineOccupationActivity sectorsGovernmentDescriptionCompetenciesLegislationRelated jobsGovernment official, President of Ukraine Politics of Ukraine Constitution Human rights Presidency President Volodymyr Zelenskyy Office of the President National Security and Defence Council Presidential representatives Presidential symbols Executive Prime Minister Denys Shmyhal Cabinet Shmyhal Government Legislature Verkhovn...

County in Kentucky, United States This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Oldham County, Kentucky – news · newspapers · books · scholar · JSTOR (September 2016) (Learn how and when to remove this message) County in KentuckyOldham CountyCountyOldham County courthouse in La Grange FlagSealLocation with...

Newfoundland lawyer, politician and judge William WarrenWarren, circa 19237th Prime Minister of NewfoundlandIn officeJuly 24, 1923 – May 7, 1924MonarchGeorge VGovernorWilliam AllardycePreceded byRichard SquiresSucceeded byAlbert Hickman Personal detailsBorn(1879-10-09)October 9, 1879DiedDecember 31, 1927(1927-12-31) (aged 48)NationalityNewfoundlanderPolitical partyLiberal Reform Party William Robertson Warren (October 9, 1879 – December 31, 1927) was a Newfoundland lawye...

Manusia[1] Periode 0,35–0 PreЄ Є O S D C P T J K Pg N Pleistosen Tengah – Kini Homo sapiens Laki-laki (kiri) dan perempuan (kanan) dari Suku Akha di utara ThailandRekaman TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoPrimatesFamiliHominidaeGenusHomoSpesiesHomo sapiens Linnaeus, 1758 Tata namaSinonim takson Sinonim spesies[1] aethiopicusBory de St. Vincent, 1825 americanusBory de St. Vincent, 1825 arabicusBory de St. Vincent, 1825 aurignacensisKlaatsch & Haus...

Carlos ReutemannReutemann di Monza pada 1981 Senator NasionalMasa jabatan10 Desember 2003 – 7 Juli 2021Daerah pemilihanSanta FeGubernur Santa FeMasa jabatan10 Desember 1999 – 10 Desember 2003PendahuluJorge ObeidPenggantiJorge ObeidMasa jabatan10 Desember 1991 – 10 Desember 1995PendahuluVíctor ReviglioPenggantiJorge Obeid Informasi pribadiLahir(1942-04-12)12 April 1942Santa Fe, ArgentinaMeninggal7 Juli 2021(2021-07-07) (umur 79)Santa Fe, Argentina Karier ...
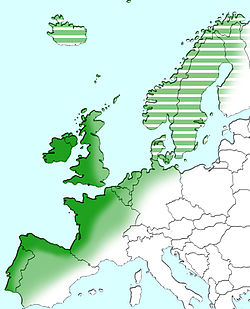
Geographical region of Europe Floristic regions in Europe Atlantic Europe is a geographical term for the western portion of Europe which borders the Atlantic Ocean. The term may refer to the idea of Atlantic Europe as a cultural unit and/or as a biogeographical region. It comprises the Atlantic Isles (Great Britain and Ireland), Iceland, Belgium, the Netherlands, the central and northern regions of Portugal, northwestern and northern Spain (including Galicia, Asturias, Cantabria, Southern Bas...

Japanese baseball player Not to be confused with Tetsuya Shiokawa. Baseball player Tatsuya ShiokawaTohoku Rakuten Golden Eagles – No. 86Infielder / CoachBorn: (1983-03-15) March 15, 1983 (age 41)Kobe, JapanBatted: SwitchThrew: RightNPB debutJune 1, 2006, for the Tohoku Rakuten Golden EaglesLast appearanceJune 6, 2011, for the Tohoku Rakuten Golden EaglesNPB statisticsBatting average.199Home runs1RBIs13Stolen Bases16 TeamsAs player Tohoku Rakuten Golden Eag...

Shopping mall in Colorado, United StatesColorado MillsThe west entrance to the mallLocationLakewood, Colorado, United StatesCoordinates39°44′04″N 105°09′38″W / 39.734447°N 105.160430°W / 39.734447; -105.160430Address14500 W. Colfax AvenueOpening dateNovember 2002DeveloperMills CorporationManagementSimon Property GroupOwnerSimon Property Group (37.5%)No. of stores and servicesover 180No. of anchor tenants12Total retail floor area1,411,627 sq ft (13...

Graph with all vertices of degree 3 Not to be confused with graphs of cubic functions, hypercube graph, cube graph, cubical graph. The Petersen graph is a cubic graph. The complete bipartite graph K 3 , 3 {\displaystyle K_{3,3}} is an example of a bicubic graph In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs. A bicubic graph is a cubic ...

Mountain range on the Iranian–Turkmen border Kopet DagکپهداغView of the Kopet Dag in early spring from Bereket, TurkmenistanHighest pointPeakKuh-e QuchanElevation3,191 m (10,469 ft)DimensionsLength650 km (400 mi)NamingNative nameKöpetdag; کپهداغGeographyMap of Iran showing the location of Kopet Dag. CountriesTurkmenistan and IranRange coordinates38°4′N 57°22.4′E / 38.067°N 57.3733°E / 38.067; 57.3733 Map of Iran wit...

Questa voce sull'argomento stagioni delle società calcistiche francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Voce principale: Athlétic Club arlésien. A.C. Arles-AvignonStagione 2012-2013Sport calcio Squadra Arles-Avignon Ligue 211º posto 2011-2012 2013-2014 Si invita a seguire il modello di voce Rosa N. Ruolo Calciatore 1 P Ludovic Butelle 16 P Florent Petit 30 P Naby Yattara 3 D Nicolás Larrondo 2 D Chaher Zarour 13 D Sébastien C...

Le président Lyndon B. Johnson signe le Poverty Bill (connu aussi sous le nom d'Economic Opportunity Act) entouré par la presse et des supporteurs, le 20 août 1964. La « guerre contre la pauvreté » est proclamée par le président des États-Unis Lyndon Johnson lors de son discours sur l'état de l'Union du 8 janvier 1964. Johnson reprend alors à son compte l’objectif défini dix ans auparavant par Ida Merriam, une chercheuse qui travaillait depuis 1963 au Bureau des recher...

Dutch footballer (born 1987) Eljero Elia Elia in 2012Personal informationFull name Eljero George Rinaldo Elia[1]Date of birth (1987-02-13) 13 February 1987 (age 37)Place of birth Leidschendam-Voorburg, NetherlandsHeight 1.76 m (5 ft 9 in)[2]Position(s) WingerYouth career SV Voorburg TONEGIDO1996–2000 ADO Den Haag2000–2002 Ajax2002–2004 ADO Den HaagSenior career*Years Team Apps (Gls)2004–2007 ADO Den Haag 59 (6)2007–2009 Twente 64 (11)2009–2011 H...











