Esforço interno
|
Read other articles:

Exercise by Nazi Germany to forge British bank notes A £5 note (White fiver) forged by Sachsenhausen concentration camp prisoners Operation Bernhard was an exercise by Nazi Germany to forge British bank notes. The initial plan was to drop the notes over Britain to bring about a collapse of the British economy during the Second World War. The first phase was run from early 1940 by the Sicherheitsdienst (SD) under the title Unternehmen Andreas (Operation Andreas). The unit successfully duplica...

La complexité caractérise le comportement d'un système dont les composants interagissent localement et de façon non linéaire, ce qui se traduit par un comportement difficilement prédictible[1]. La complexité peut donc caractériser un système « composé d'un grand nombre d'éléments interagissant sans coordination centrale, sans plan établi par un architecte, et menant spontanément à l'émergence de structures complexes » (Alain Barrat, directeur de recherche au Centre...

العلاقات البالاوية الغينية بالاو غينيا بالاو غينيا تعديل مصدري - تعديل العلاقات البالاوية الغينية هي العلاقات الثنائية التي تجمع بين بالاو وغينيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة بالاو غيني...

دولار ليبيري5 دولار ليبيريةمعلومات عامةالبلد ليبيريا المنطقة ليبيريا رمز العملة Lib$L$ رمز الأيزو 4217 LRD المصرف المركزي البنك المركزي الليبيري سعر الصرف 0٫005429 يورو (3 فبراير 2019) العملات المعدنية 5، 10، 25، 50، سنت، دولار واحد[1]تعديل - تعديل مصدري - تعديل ويكي بيانات الدولار الل�...

Synthetic estrogen brand Not to be confused with Quinestrol. QuinestradolClinical dataTrade namesColpovis, Colpovister, PentovisOther namesQuinestradiol; Quinestriol; Estriol 3-cyclopentyl ether; E3CPERoutes ofadministrationBy mouthDrug classEstrogen; Estrogen etherATC codeNoneIdentifiers IUPAC name (8R,9S,13S,14S,16R,17R)-3-cyclopentyloxy-13-methyl-6,7,8,9,11,12,14,15,16,17-decahydrocyclopenta[a]phenanthrene-16,17-diol CAS Number1169-79-5 YPubChem CID14431ChemSpider16735993UNII422L8173W...
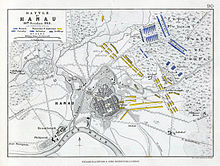
1813 battle during the War of the Sixth Coalition Battle of HanauPart of the German campaign of the Sixth CoalitionBattle of Hanau, Horace VernetDate30–31 October 1813LocationHanau, Duchy of Frankfurt50°07′59″N 8°55′01″E / 50.1331°N 8.9169°E / 50.1331; 8.9169Result French victoryBelligerents France Bavaria AustriaCommanders and leaders Napoleon Bonaparte Karl von WredeStrength 17,000-30,000 43,000Casualties and losses 4,500[1]-5,0...

Hair product brand This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pantene – news · newspapers · books · scholar · JSTOR (April 2023) (Learn how and when to remove this message) PanteneProduct typeHair careOwner Procter & GambleProduced by Richardson Vicks (1985) Procter & Gamble (1985–present...

Cet article est une ébauche concernant l’île de Pâques. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Ahu Vinapu Vue générale de l'édifice Présentation Type Ahu Caractéristiques Matériaux Pierres Géographie Coordonnées 27° 10′ 35″ sud, 109° 24′ 23″ ouest Pays Chili Géolocalisation sur la carte : île de Pâques Ahu Vinapu modifier Ahu Vinapu est ...

American big-wave surfer Laird HamiltonPersonal informationBornLaird John Zerfas (1964-03-02) March 2, 1964 (age 60)San Francisco, California, U.S.ResidenceKauai and MalibuHeight6 ft 3 in (191 cm)Weight215 lb (98 kg)Surfing careerYears active1970–presentSponsorsOxbow, AmwayMajor achievements Co-invented Tow-in surfing Heaviest wave ever ridden successfully: Teahupo'o, August 17, 2000 Surfing specificationsStanceRegular (natural foot)QuiverLong boardsFavorit...

这是马来族人名,“莫哈末”是父名,不是姓氏,提及此人时应以其自身的名“马哈迪”为主。阿拉伯语“本”(bin)或“伊本”(ibn)、“宾蒂”(binti),意为后者是前者“某某之子”或“某某之女”。 尊敬的 敦马哈迪·莫哈末Mahathir bin Mohamad博士DK SMN SPMJ SSAP DGSM SPNS DUPN SPDK2018年的马哈迪馬來西亞第4、7任首相任期2018年5月10日—2020年3月1日辭職看守:2020年2月24日-2020�...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Railway station in Kumamoto, Japan Musashizuka Station武蔵塚駅Musashizuka Station in 2014General informationLocationJapanCoordinates32°51′00″N 130°46′12″E / 32.85000°N 130.77000°E / 32.85000; 130.77000Operated by JR KyushuLine(s)■ Hōhi Main LineDistance12.9 km from KumamotoPlatforms2 side platformsTracks2ConstructionStructure typeAt gradeBicycle facilitiesBike shedOther informationStatusStaffed ticket window (Midori no Madoguchi)(outsourced)WebsiteOf...

Presiden Venezuela (bahasa Spanyol: Presidente de Venezuela) adalah sebutan politis untuk kepala negara dan kepala pemerintahan Venezuela. Masa jabatan presiden yang berlaku sekarang adalah enam tahun dengan kemungkinan untuk satu kali lagi langsung dipilih kembali, dan dengan jaminan konstitusional untuk menyelenggarakan referendum setiap saat pada masa tiga tahun terakhir dari masa jabatan presiden itu. Sebutan Presiden mencakup hanya orang-orang yang diambil sumpahnya untuk menduduki jabat...

جوليان ستيفان (بالفرنسية: Julien Stéphan) معلومات شخصية الميلاد 18 سبتمبر 1980 (العمر 43 سنة)[1]رين الطول 1.75 م (5 قدم 9 بوصة) مركز اللعب وسط الجنسية فرنسا الأب غاي ستيفان المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1998–2001 أكاديمية باريس سان جيرمان 6 (0) 2001–2002 تولوز ...

Building in Manhattan, New York Not to be confused with 689 Fifth Avenue, once known as the Aeolian Building. Aeolian BuildingGeneral informationLocationManhattan, New York CityCoordinates40°45′16″N 73°58′56″W / 40.7544°N 73.9822°W / 40.7544; -73.9822Opened1912Height260 feet (79 m)Technical detailsFloor count18Design and constructionArchitect(s)Warren and Wetmore The Aeolian Building is a skyscraper in Midtown Manhattan in New York City, at 29–33 West 42n...

Pour les articles homonymes, voir Mondes possibles (homonymie). Cet article est une ébauche concernant la philosophie et la logique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Le triangle de Penrose, un objet impossible… dans notre monde. Exemple de construction du triangle de Penrose dans la réalité (cassure). Les théories des mondes possibles sont des théories élaborant la possibilité qu'existent...

Voce principale: XVII Giochi del Mediterraneo. Le gare di canoa/kayak ai XVII Giochi del Mediterraneo si sono svolte il 27 e il 29 giugno 2013 alla boathouse nella Çukurova Üniversitesi. Si è gareggiato in sei categorie diverse, di cui quattro maschili e due femminili, tutte kayak. Indice 1 Calendario 2 Risultati 2.1 Uomini 2.2 Donne 3 Medagliere 4 Collegamenti esterni Calendario Le gare hanno seguito il seguente calendario: ● Competizioni ● Finali Giugno 18 19...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (ديسمبر 2021) محمد تانكو معلومات شخصية الميلاد 15 نوفمبر 1988 (العمر 35 سنة)غانا الطول 6 قدم 0 بوصة (1.83 م) مركز اللعب مهاجم الجنسية غانا معلومات النادي النادي الح�...

American academic and political activist (born 1944) For other people named Angela Davis, see Angela Davis (disambiguation). Angela Davis1974 portrait of Davis by Bernard GotfrydBornAngela Yvonne Davis (1944-01-26) January 26, 1944 (age 80)Birmingham, Alabama, U.S.EducationBrandeis University (BA)University of FrankfurtUniversity of California, San Diego (MA)OccupationsActivistscholarPolitical partyCCDS (since 1991)Other politicalaffiliationsCommunist Party USA (1969–1991)Black Panther...









![{\displaystyle [T]_{xyz}={\begin{bmatrix}\sigma _{x}&\tau _{y}&\tau _{z}\\\tau _{y}&0&0\\\tau _{z}&0&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc30a70c396f407e7a356d14086849d70b54eadd)











![{\displaystyle {\begin{cases}m_{x}=-D\left[{\cfrac {\partial ^{2}w}{\partial x^{2}}}+\nu {\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]&m_{xy}=-D(1-\nu )\left[{\cfrac {\partial ^{2}w}{\partial y\partial x}}\right]\\m_{y}=-D\left[\nu {\cfrac {\partial ^{2}w}{\partial x^{2}}}+{\cfrac {\partial ^{2}w}{\partial y^{2}}}\right]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a416bd98bcd3be344d4c29fbaa0e44a29891b52f)




