Contraexemplo
|
Read other articles:

Ahmad Rizal Ramdhani Kepala Staf Komando Gabungan Wilayah Pertahanan II ke-5Masa jabatan29 Juli 2022 – 29 Maret 2023 PendahuluMuhammad Saleh MustafaPenggantiAchmad WibisonoAsisten Deputi Koordinasi Pengelolaan Pemilu dan Penguatan Partai PolitikMasa jabatan2021 – 29 Juli 2022 PendahuluYusran YunusPenggantiHaryadiKomandan Korem 162/Wira BhaktiMasa jabatan2018–2021 PendahuluFarid MakrufPenggantiLalu Rudy Irham Srigede Informasi pribadiLahir19 November 1970 (umur ...

Beberapa busana yang digunakan untuk Balet Triadik Balet Triadik (bahasa Jerman: Triadisches Ballett) adalah balet yang dikembangkan oleh Oskar Schlemmer. Pertunjukan perdananya digelar di Stuttgart pada 30-31 September 1922, diiringi karya musik Paul Hindemith, setelah sejumlah penampilan sejak 1916. Balet ini menjadi tarian garda depan yang paling banyak dipertunjukkan. Ketika Schlemmer berkegiatan di Bauhaus pada 1921-1929, bersamaan dengan tur pertunjukannya, balet ini juga menyebarluaska...

Head of the Catholic Church from c. 99 to c. 107 Aristus redirects here. For other people with this name, see Aristus (disambiguation). Pope SaintEvaristusBishop of RomePope Evaristus, 15th centuryChurchEarly ChurchPapacy beganc. 99Papacy endedc. 107PredecessorClement ISuccessorAlexander IPersonal detailsBornBethlehem, JudeaDiedc. 107Rome, Roman EmpireSainthoodFeast day26 October Pope Evaristus (Greek: Ευάριστος) was the bishop of Rome from c. 99 to his death c. 107.[1][2...

Экономика Нигерии Лагос - экономическая столица Нигерии Валюта Найра Международныеорганизации ОПЕК, АС, ВТО, СССГ, Содружество Статистика ВВП $398,19 млрд (номинал, 2018)[1] $1168,75 млрд (ППС, 2018)[1] Рост ВВП ▲ 4 % (2015)[2] ВВП на душу населения $2033 (номинал, 2018)[1] $5967 (ППС...

2007 video game For the games at a carnival, see Carnival game. 2007 video gameCarnival GamesNorth American Wii box artDeveloper(s)Cat Daddy GamesPublisher(s)Global Star Software (Wii)2K (DS, iPhone)Platform(s)Wii, Nintendo DS, iOS (iPhone)ReleaseWiiNA: August 27, 2007AU: October 19, 2007EU: October 26, 2007DSNA: July 8, 2008EU: August 22, 2008AU: September 4, 2008iPhoneAugust 5, 2010Genre(s)PartyMode(s)Single-player, multiplayer Carnival Games (known in Europe and Australia as Carnival Funfa...

العلاقات الإماراتية الليختنشتانية الإمارات العربية المتحدة ليختنشتاين الإمارات العربية المتحدة ليختنشتاين تعديل مصدري - تعديل العلاقات الإماراتية الليختنشتانية هي العلاقات الثنائية التي تجمع بين الإمارات العربية المتحدة وليختنشتاين.[1][2][3&#...

Hamletposter teatrikalSutradaraLaurence OlivierProduserLaurence OlivierSkenarioLaurence Olivier(tidak disebutkan)BerdasarkanHamlet (permainan panggung)oleh William ShakespearePemeranLaurence OlivierPenata musikWilliam WaltonSinematograferDesmond DickinsonPenyuntingHelga CranstonPerusahaanproduksiTwo CitiesDistributorRank Film Distributors Ltd. (UK)Universal-International (US)Tanggal rilis 4 Mei 1948 (1948-05-04) Durasi155 menitNegaraBritania RayaBahasaInggrisAnggaran£527,530&...

Stasiun Funagata舟形駅Stasiun Funagata pada Mei 2005Lokasi391-2, Funagata, Funagata-machi, Mogami-gun, Yamagata-ken 999-4601JepangKoordinat38°41′30″N 140°18′58″E / 38.691708°N 140.316106°E / 38.691708; 140.316106Koordinat: 38°41′30″N 140°18′58″E / 38.691708°N 140.316106°E / 38.691708; 140.316106Operator JR EastJalur■ Jalur Utama ŌuLetak140.3 kilometer dari FukushimaJumlah peron2 peron sisiInformasi lainStatusMemilik...

Warwickshire shown within England Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) There are over 9,000 Grade I listed buildings in England. This page is a list of these buildings in the county of Warwickshire, by district. North Warwickshire Name Location Type Completed [note 1]Date designated Grid ref.[note 2]Geo-coordinates Entry number [note 3]Image Church of St Mary th...

Person temporarily living abroad Expat redirects here. For the XML parser, see Expat (software). For the free software license, see Expat License. For other uses, see Expatriate (disambiguation). Expatriate French voters queue in Lausanne, Switzerland, for the first round of the presidential election of 2007. An expatriate (often shortened to expat) is a person who temporarily resides outside their country of citizenship.[1] The term often refers to a professional, skilled worker, or ...

Medical school of the University of Florida College of MedicineTypePublic medical schoolEstablished1956Parent institutionUniversity of FloridaEndowment$1.73 billion (2018)[1]DeanColleen G. KochStudents1,642 [2]LocationGainesville, Florida, United StatesWebsitemed.ufl.edu Entrance to the College of Medicine Teaching Hospital University of Florida Cancer Hospital Medical Plaza The University of Florida College of Medicine is the medical school of the University of Florida. It is...
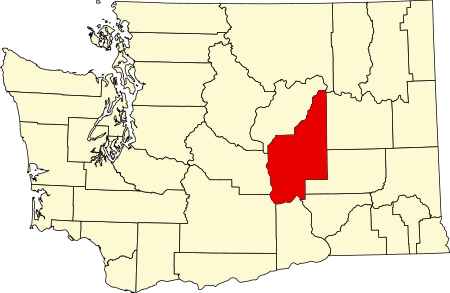
Эта статья об округе в штате Вашингтон; другие значения: Грант (округ). ОкругГрантангл. Grant County 47°13′ с. ш. 119°28′ з. д.HGЯO Страна США Входит в штат Вашингтон Адм. центр Эфрейта[англ.] История и география Дата образования 24 февраля 1909 Площадь 7229 км² (6944 км² — с�...

Italian businessperson (born 1962) Marco BizzarriBizzarri in 2018Born9 August 1962 (1962-08-09) (age 61)Reggio Emilia, ItalyYears active1986–presentTitlePresident and CEO, GucciBoard member ofKering Marco Bizzarri (born 19 August 1962) is an Italian business executive, president and CEO of Gucci since January 2015 till December 2023.[1] He previously was president and CEO of Stella McCartney (2005–2009) and Bottega Veneta (2009–2014), and joined Kering's exec...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

اضغط هنا للاطلاع على كيفية قراءة التصنيف ضفدع مونتي زوما النمري حالة الحفظ أنواع غير مهددة أو خطر انقراض ضعيف جدا [1] المرتبة التصنيفية نوع التصنيف العلمي النطاق: حقيقيات النوى المملكة: حيوانات الشعبة: حبليات الشعيبة: فقاريات الطائفة: برمائيات الرتبة: بتراوا...

British peer and Conservative Party politician His GraceThe Duke of PortlandKGPortrait by Philip de László, 1914Born(1893-03-16)16 March 1893Mayfair, London, EnglandDied21 March 1977(1977-03-21) (aged 84)Welbeck Abbey, Nottinghamshire, EnglandSpouse(s) Ivy Gordon-Lennox (m. 1915)IssueLady Anne Cavendish-BentinckLady Victoria BentinckParentsWilliam Cavendish-Bentinck, 6th Duke of PortlandWinifred Anna Dallas-Yorke William Arthur Henry Cavendish-Bentinck, 7...

Oud Eik en Duinen pada bulan April 2004 Oud Eik en Duinen adalah sebuah pemakaman di Den Haag, Belanda, yang sebelumnya bernama Eik en Duinen dan juga dijuluki Père-Lachaise di Belanda. Pemakaman ini dibangun di sekitar sebuah kapel yang didirikan sekitar tahun 1247 oleh Willem II dari Belanda untuk mengenang ayahnya, Florens IV, Pangeran Belanda. Sebagian kapel ini dibongkar pada tahun 1581, dan pada abad ke-17 daerah ini digunakan sekali lagi sebagai pemakaman. Ketika Eik dan Duinen penuh,...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Meridian High School Idaho – news · newspapers · books · scholar · JSTOR (April 2009) (Learn how and when to remove this message) Public school in Meridian, Idaho, United StatesMeridian High SchoolAddress1900 West Pine AvenueMeridian, Idaho 83642United Sta...

English novelist and writer (1867–1940) E. F. BensonOBEBornEdward Frederic Benson(1867-07-24)24 July 1867Wellington College, Berkshire, EnglandDied29 February 1940(1940-02-29) (aged 72)University College Hospital, London, EnglandOccupationWriterNotable worksMapp and Lucia seriesDodo seriesSupernatural horror storiesNotable awardsOBERelativesEdward White Benson (father)Mary Benson (mother)Robert Hugh Benson (brother)A. C. Benson (brother)Margaret Benson (sister) Edward Frederic Benson O...

Du khách tới Pakistan phải xin thị thực từ một trong những phái bộ ngoại giao của Pakistan.[1] Phái bộ ngoại giao của Pakistani tại nước ngoài cung cấp nhiều loại thị thực, và một số du khách có thể xin thị thực tại cửa khẩu nếu họ đi theo tour hoặc đi công tác. Pakistan không cung cấp thị thực tại cửa khẩu cho khách du lịch đi lẻ, mặc dù công dân một số quốc gia được miễn th�...


