Configuração de grafos

Esta página ou se(c)ção precisa ser formatada para o padrão wiki. Por favor ajude a formatar esta página de acordo com as diretrizes estabelecidas. (Julho de 2012)

Configuração de grafos é uma ferramenta teórica usada na teoria da complexidade computacional para provar a relação entre o problema de alcance dos grafos e a complexidade de classes.

Definição

Um modelo teórico computacional, como uma máquina de Turing ou autômato finito, explica como executar um processo de computação. Os modelos explicam o que significa uma configuração inicial da máquina e quais passos podem ser dados para continuar a computação, até que eventualmente pare. Uma configuração, também chamada de descrição instantânea (ID) é uma representação finita da máquina em um determinado tempo. Por exemplo, para um autômato finito, dado uma entrada, a configuração será o estado atual e o numero de letras lidas, para uma máquina de Turing será o estado, o conteúdo da fita e a posição da cabeça da leitora. Um grafo de configuração é um grafo dirigido rotulado onde o rótulo dos vértices são as configurações possíveis dos modelos e onde existe uma aresta de uma configuração para outra se corresponder a um passo computacional do modelo.

A configuração de aceitação e inicial da máquina são vértices especiais do grafo de configuração. A computação aceita se e somente se existe um caminho de um vértice inicial para um vértice de aceitação.

Propriedades úteis

Se a computação é determinística, então para qualquer computação, existe no máximo, um passo possível, de modo que o grafo é de grau um, e existe um estado inicial. Uma vez que adicionamos um vértice inicial falso com uma aresta conectando para todos os outros vértices iniciais e um vértice de aceitação falso com uma aresta conectando para todos os outros vértices de aceitação, checando se existe uma computação de aceitação só será necessário verificar se existe um caminho do vértice inicial para o vértice de aceitação, o qual é um problema de alcance. Um ciclo no grafo significa que existe um possível loop infinito na computação. O grafo computacional pode ser de tamanho infinito se não existem restrições de configurações possíveis; na verdade, é fácil ver que existem máquinas de Turing que podem chegar a grandes configurações arbitrariamente. Também é possível ter grafos infinitos: em autômatos finitos, a configuração é composta pela posição da cabeça de leitura e o estado atual, de modo que o grafo de configuração é do tamanho $O(n)$ . ^[1]

Uso da ferramenta

Esta noção é útil, pois reduz os problemas computacionais para problemas de alcance de grafos. Por exemplo, desde que o problema do alcance esteja em NL, podemos representar configurações em espaço logarítmico no tamanho da entrada, e desde que a configuração da máquina de Turing em NL é de fato do tamanho logarítmico, então o alcance dos grafos esta completa para NL. ^[2] Na outra direção, o que ajuda a verificar a complexidade do modelo de computação; a decisão do problema para um modelo (determinístico) cuja configuração é do espaço logarítmico de acordo com a entrada está em (L) NL. Este é por exemplo o caso do o autômato finito e do autômato finito com um contador.

Referências

↑ Arora, Sanjeev. (2009). Computational complexity : a modern approach. Cambridge: Cambridge University Press. OCLC 286431654
↑ Papadimitriou, Christos H. (1994). Computational Complexity, Reading, Massachusetts: Addison-Wesley. ISBN 0-201-53082-1.

Read other articles:

Choi Yoo-jung (penyanyi)

Untuk orang lain dengan nama yang sama, lihat Choi Yoo-jung. Dalam nama Korean ini, nama keluarganya adalah Choi. Choi Yoo-jungChoi di bulan February 2019Nama asal최유정LahirChoi Yoo-jung12 November 1999 (umur 24)[1]Guri, Provinsi Gyeonggi, Korea SelatanPendidikanSchool of Performing Arts SeoulPekerjaanPenyanyipenariaktrisTahun aktif2016–sekarangNama KoreaHangul최유정 Hanja磪有情 Alih AksaraChoe Yu-jeongMcCune–ReischauerCh'oe Yujŏng Choi Yoo-jung (최유�...

Repubblica Popolare Socialista d'Albania

Albania (dettagli) (dettagli) Motto: (SQ) Proletarë të të gjitha vendeve, bashkohuni!(IT) Proletari di tutto il mondo, unitevi! Albania - Localizzazione Dati amministrativiNome completoRepubblica Popolare d'Albania (1946-1976) Repubblica Popolare Socialista d'Albania (1976-1991) Nome ufficialeRepublika Popullore e Shqipërisë (1946-1976) Republika Popullore Socialiste e Shqipërisë (1976-1991) Lingue ufficialialbanese Lingue parlatealbanese InnoHymni i Flamurit CapitaleTirana PoliticaFor...

The Shrike (film)

1955 film by José Ferrer The ShrikeTheatrical release posterDirected byJosé FerrerScreenplay byKetti FringsBased onThe Shrikeby Joseph KrammProduced byAaron RosenbergStarringJosé FerrerJune AllysonCinematographyWilliam Daniels, A.S.C.Edited byFrank Gross, A.C.E.Music byFrank SkinnerProductioncompanyUniversal International PicturesDistributed byUniversal PicturesRelease date June 16, 1955 (1955-06-16) Running time88 minutesCountryUnited StatesLanguageEnglish The Shrike is a 1...

Act of Valor

Act of ValorPoster rilis teatrikalSutradaraMike McCoyScott WaughProduserMike McCoyScott WaughDitulis olehKurt JohnstadPemeranRoselyn SánchezNestor SerranoEmilio RiveraRorke DenverPenata musikNathan FurstSinematograferShane HurlbutPenyuntingSiobhan PriorMichael TronickScott WaughPerusahaanproduksiBandito BrothersDistributorRelativity MediaTanggal rilis 24 Februari 2012 (2012-02-24) Durasi110 menitNegaraAmerika SerikatBahasaInggrisAnggaran$12 juta[1]Pendapatankotor$81,272,76...

Nilai-nilai Jepang

Nilai-nilai Jepang (日本的価値観code: ja is deprecated ) adalah tujuan budaya, keyakinan, dan perilaku yang dianggap penting dalam budaya Jepang. Perspektif global Negara menurut perbedaan dalam indeks nilai emansipatif dengan Jepang.[1] +1.5 to +0.2 +0.1 to +1.5 +0.5 to +0.1 0 to +0.5 0 0 to −0.05 −0.05 to −0.1 −0.1 to −0.15 −0.15 to −0.2 −0.2 ...

Доисторическая Польша

История ПольшиДоисторический периодСредние века Гнезненское государство Королевство Польское Польские княжества 1320—1386 Новое время Речь Посполитая Саксонский период 1764—1795 Великое Герцогство Варшавское Царство Польское Вольный город Краков Вольный город Гданьс�...

Chevrolet Venture

Cet article est une ébauche concernant l’automobile. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Chevrolet Venture Appelé aussi Chevrolet Trans SportOpel SintraBuick GL8Oldsmobile SilhouettePontiac Trans SportPontiac MontanaVauxhall Sintra Marque Chevrolet Opel Buick Oldsmobile Pontiac Vauxhall Années de production 1997 - 2005 Classe Mon...

Andrew H. Burke

American politician (1850–1918) Andrew Horace BurkeFrom the 1897 atlas North Dakota and Richland County Chart2nd Governor of North DakotaIn officeJanuary 7, 1891 – January 3, 1893LieutenantRoger AllinPreceded byJohn MillerSucceeded byEli C. D. Shortridge Personal detailsBorn(1850-05-15)May 15, 1850New York City, U.S.DiedNovember 17, 1918(1918-11-17) (aged 68)Roswell, New Mexico, U.S.Political partyRepublicanSpouseCaroline ClevelandAlma materDePauw UniversityProfessionPol...

RAB27A

Protein-coding gene in the species Homo sapiens RAB27AIdentifiersAliasesRAB27A, GS2, HsT18676, RAB27, RAM, member RAS oncogene familyExternal IDsOMIM: 603868 MGI: 1861441 HomoloGene: 3069 GeneCards: RAB27A Gene location (Human)Chr.Chromosome 15 (human)[1]Band15q21.3Start55,202,966 bp[1]End55,319,113 bp[1]Gene location (Mouse)Chr.Chromosome 9 (mouse)[2]Band9 D|9 40.08 cMStart72,952,136 bp[2]End73,004,911 bp[2]RNA expression patternBgeeHumanM...

Joseph Marie de Barral

Pour les articles homonymes, voir Famille de Barral et Barral. Joseph Marie de Barral Fonctions Maire de Grenoble 28 février 1790 – 1er août 1790 (5 mois et 4 jours) décembre 1792 – mai 1794 (1 an et 5 mois) 1800 – 1800 (moins d'un an) Député de l'Isère 27 décembre 1803 – 4 juin 1814 (10 ans, 5 mois et 8 jours) Législature Corps législatif (Consulat et Premier Empire) Biographie Date de naissance 21 mars 1742 Lieu de naissance Grenoble, Dau...

IRAK2

Protein-coding gene in humans IRAK2Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes3MOPIdentifiersAliasesIRAK2, IRAK-2, interleukin 1 receptor associated kinase 2External IDsOMIM: 603304 MGI: 2429603 HomoloGene: 1207 GeneCards: IRAK2 Gene location (Human)Chr.Chromosome 3 (human)[1]Band3p25.3Start10,164,919 bp[1]End10,243,745 bp[1]Gene location (Mouse)Chr.Chromosome 6 (mouse)[2]Band6 E3|6 52.82 cMStart113,615,428 bp[2]End113,67...

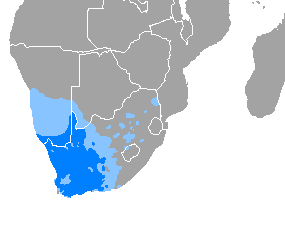
Bahasa Afrikaans

Bahasa AfrikaansPengucapan[afriˈkɑːns]Dituturkan diAfrika Selatan, Namibia, Botswana, Zambia, ZimbabweEtnis Afrikaners Boers Basters Cape Coloureds Melayu Cape Griqua Goffal Penutur7,2 juta (2023)[1]18,8 juta penutur L2 diseluruh Afrika Selatan (2002)[2] Rumpun bahasaIndo-Eropa JermanikJermanik BaratWeser-RhineFranka HilirBelandaBelanda IntiHollandikBahasa Afrikaans Bentuk awalFranka Belanda KunoBelanda PertengahanBelanda ModernBahasa Afrikaans Sistem penulisanAlf...

لعبة الحب (فيلم)

لعبة الحبمعلومات عامةالصنف الفني فيلم كوميدي[1] — فيلم رومانسي[1] تاريخ الصدور 23 أكتوبر 2006مدة العرض 80 دقيقة[1] اللغة الأصلية العربيةالبلد مصرالطاقمالمخرج محمد علي الكاتب أحمد الناصرسامي حسامالبطولة هند صبريخالد أبو النجابسمةبشرىصناعة سينمائيةالمنتج الشر�...

List of popcorn brands

An uncooked bag of microwave popcorn This is a list of notable popcorn brands. Popcorn, also known as popping corn, is a type of corn (maize, Zea mays var. everta) that expands from the kernel and puffs up when heated. Popcorn is able to pop because its kernels have a hard moisture-sealed hull and a dense starchy interior. Pressure builds inside the kernel, and a small explosion (or pop) is the end result. Some strains of corn are now cultivated specifically as popping corns. Microwave popco...

عصر (جيولوجيا)

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. لمعانٍ أخرى، طالع عصر (توضيح). العصر[1] الجيولوجي هو أحد الأقسام الفرعية للزمن الجيولوجي لتحديد زمن تشكل الصخور والأحداث الجيولوجية من مكان إلى آخر.[2][3] تشك�...

MXM (musical duo)

2017–2018 South Korean musical duo MXMBackground informationOriginSeoul, South KoreaGenresK-pophip hopR&B[1]tropical houseYears active2017 (2017)–2018LabelsBrand NewMembers Lim Young-min Kim Dong-hyun Websitebrandnewmusic.co.kr MXM was a South Korean duo under Brand New Music that consisted of members Lim Young-min and Kim Dong-hyun.[2][3][4] History Pre-debut Lim Young-min and Kim Dong-hyun met as trainees under Brand New Music. They represented t...

加勒比人

Carib family (by John Gabriel Stedman) 加勒比人，又譯卡利勃人，是小安的列斯群島（Lesser Antilles）的居民，也是「加勒比海」名字的來源。他們是美洲原住民的一支，起源於西印度地區到南美洲的北海岸一帶。雖然加勒比男人通常使用任一種加勒比語（Cariban languages）或混合語（pidgin），但加勒比族過去經常對外侵略，擁有許多阿拉瓦女性（Arawak）俘虜，所以Kalhíphona（一種Maipurean...

World Trade Centre Residence

Artikel ini membahas mengenai bangunan, struktur, infrastruktur, atau kawasan terencana yang sedang dibangun atau akan segera selesai. Informasi di halaman ini bisa berubah setiap saat (tidak jarang perubahan yang besar) seiring dengan penyelesaiannya. World Trade Centre ResidenceWorld Trade Centre Residence tanggal 2 November 2007Informasi umumStatusSelesai dibangunLokasiDubai, Uni Emirat ArabPembukaan2008TinggiMenara antena158 m (518 kaki)Data teknisJumlah lantai38Desain dan konst...

Henri Cartier-Bresson

French photographer (1908–2004) Henri Cartier-BressonHenri in 1972Born(1908-08-22)22 August 1908Chanteloup-en-Brie, FranceDied3 August 2004(2004-08-03) (aged 95)Céreste, FranceBurial placeMontjustin, FranceAlma materLycée Condorcet, ParisOccupationsPhotographerpainterSpouses Ratna Mohini (m. 1937; div. 1967) Martine Franck (m. 1970) Children1Awards Grand Prix National de la Photographie (1981) Has...

Kuzu no Honkai

Kuzu no HonkaiGambar sampul manga volume pertama menampilkan Hanabi Yasuraokaクズの本懐(Kuzu no Honkai)GenrePsikologis[1]Drama roman[2] MangaPengarangMengo YokoyariPenerbitSquare EnixPenerbit bahasa InggrisNA Yen PressMajalahBig GanganDemografiSeinenTerbit25 September 2012 – 25 Maret 2017Volume8 Seri animeSutradaraMasaomi AndōProduserNaoyasu FujiyamaGō WakabayashiShota KomatsuSkenarioMakoto UezuMusikMasaru YokoyamaStudioLerchePelisensiAmazon Video (streaming)AUS Madma...