Cipriano José Veloso

Filho de José Joaquim Vellozo, era natural da província da Bahia, onde nasceu em 1797. Na grafia original, seu nome se escreve Cypriano José Vellozo. Matriculou-se, em 1819, na Faculdade de Leis da Universidade de Coimbra, onde recebeu o grau de Bacharel em carta de 22 de junho de 1824.Regressando ao Brasil, foi nomeado, por D. Pedro I, Ouvidor da comarca do Rio Grande do Norte, em decreto de 19 de outubro de 1824; obteve a nomeação de Provedor da Fazenda dos Defuntos e Ausentes, Resíduos e Capelas, em alvará de 8 de março de 1827.

Foi nomeado Desembargador da Relação do Maranhão, em decreto de 12 de outubro de 1827; continuou pertencendo à mesma Relação, conforme determinou a portaria de 14 de março de 1833. Havendo sido criado, em Decreto nº 1.597, de 1º de maio de 1855, um Tribunal de Comércio na província do Maranhão, D. Pedro II, em decreto de 22 de junho desse ano, resolveu nomear Cypriano Vellozo para Presidente do mesmo tribunal.

Foi nomeado Ministro do Supremo Tribunal de Justiça (STJ), em decreto de 25 de setembro de 1857, preenchendo a vaga ocorrida com o falecimento de Francisco José Alves Carneiro; tomou posse a 19 de dezembro do mesmo ano. Foi agraciado com o foro de Fidalgo Cavaleiro, em decreto de 9 de junho de 1857, e comenda da Ordem de Cristo, em decreto de 29 de setembro de 1859. Faleceu no Rio de Janeiro, a 16 de agosto de 1861, sendo sepultado no Cemitério de São João Batista.[1]

  1. ↑ STJ - Biografia dos Ministros - consulta em 21/08/2024 https://portal.stf.jus.br/ostf/ministros/verMinistro.asp?periodo=STJ&id=294

Read other articles:

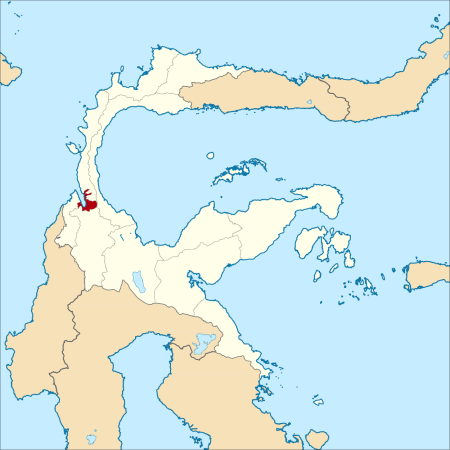
Daftar kecamatan dan kelurahan di Kota Palu

Peta Kota Palu di Sulawesi Tengah Berikut adalah daftar kecamatan dan kelurahan di Kota Palu, Provinsi Sulawesi Tengah, Indonesia. Kota Palu terdiri dari 8 Kecamatan dan 46 Kelurahan dengan luas wilayah 395,06 km² dan jumlah penduduk sebesar 363.867 jiwa dengan sebaran penduduk 921 jiwa/km².[1][2] Sebelumnya, Kota Palu terbagi atas 4 Kecamatan sesuai arah mata angin yaitu Kecamatan Palu Barat, Kecamatan Palu Timur, Kecamatan Palu Utara dan Kecamatan Palu Selatan. Empat kecam...

 

Bernardo O'Higgins

Pour les articles homonymes, voir O'Higgins et Riquelme. Bernardo O'Higgins Bernardo O'Higgins, huile de Gil de Castro. Fonctions Directeur suprême du Chili(chef de l'État) 16 février 1817 – 28 janvier 1823(5 ans, 11 mois et 11 jours) Prédécesseur José Miguel Carrera Successeur Ramón Freire Commandant en chef de l'Armée chilienne 27 avril 1819 – 28 janvier 1823(3 ans, 9 mois et 1 jour) Prédécesseur José Miguel Carrera Successeur Ramón Freire Biog...

 

Telecommunications in Zimbabwe

Communications in Zimbabwe refers to the communication services available in Zimbabwe. Background Postal and Telecommunications Regulatory Authority of Zimbabwe (POTRAZ) was established by the Postal and Telecommunications Act in 2000 and started its operations in March 2001. This legislation brought about a new institutional framework for telecommunications in Zimbabwe. Telephone system See also: Telephone numbers in Zimbabwe The phone system was once one of the best in Africa, but now suff...

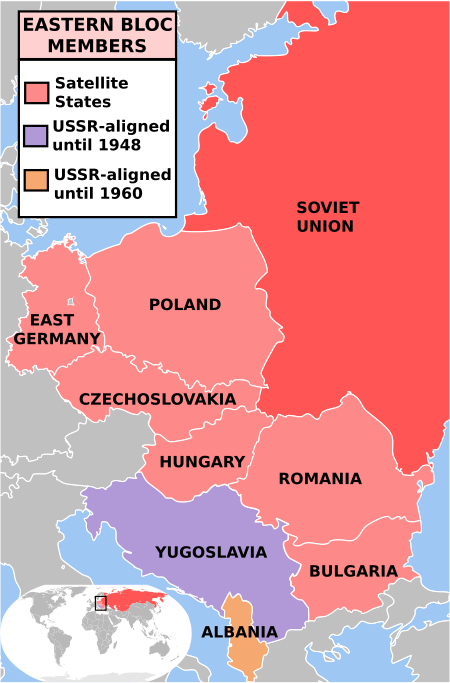
Pendudukan militer oleh Uni Soviet

Artikel ini adalah daftar dari pendudukan militer oleh Uni Soviet dari sebelum sampai sesudah Perang Dunia II[1][2][3] dan kemudian Perang Dingin. Perang Dunia II Selama periode pakta Molotov-Ribbentrop Polandia (1939–1956) Polandia adalah negara pertama yang diduduki oleh Uni Soviet selama era Perang Dunia II. Negara-negara Baltik (1940–1991) Artikel utama: Pendudukan negara-negara Baltik Teritorial Finisia (1940) Artikel utama: Republik Demokratik Finisia dan Per...

 

Сибирский горный козёл

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

 

Banijay Group

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Banijay Group – berita · surat kabar · buku · cendekiawan · JSTOR Banijay Group SASSebelumnyaBanijay Entertainment (2008–2011)JenisPerusahaan swastaIndustriHiburanPendahuluZodiak MediaEndemol Shine Gro...

Don Fanucci

Fictional character from The Godfather series Fictional character Don FanucciGastone Moschin as Don FanucciFirst appearanceThe GodfatherLast appearanceThe Godfather Part IICreated byMario PuzoPortrayed byGastone MoschinIn-universe informationNicknameDon FanucciGenderMaleOccupationExtortioner, mobsterFamilyBlack Hand Don Fanucci is a fictional character appearing in Mario Puzo's 1969 novel The Godfather and the 1974 film The Godfather Part II, a sequel to the 1972 film version of Puzo's novel....

 

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

 

The Brink (TV series)

2015 American comedy television series The BrinkPromotional posterGenrePolitical satireCreated byRoberto BenabibKim BenabibStarringJack BlackTim RobbinsPablo SchreiberAasif MandviMaribeth MonroeEric LadinGeoff PiersonEsai MoralesComposerDavid RobbinsCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes10 (list of episodes)ProductionExecutive producersRoberto BenabibJerry WeintraubJay RoachProducersDave HolsteinJack BlackTim RobbinsCamera setupSingle-cameraRunnin...

فيليب الثاني أغسطس

فيليب الثاني أغسطس (بالفرنسية: Philippe II Auguste)‏  معلومات شخصية الميلاد 21 أغسطس 1165(1165-08-21)مولن، باريس الوفاة 14 يوليو 1223 (57 سنة)مانت لا جولي  مكان الدفن كاتدرائية سان دوني  مواطنة فرنسا  الديانة مسيحية مشكلة صحية رؤية وحيدة العين  [لغات أخرى]‏  الزوجة إيزابيلا �...

 

Claisen condensation

Chemical reaction Not to be confused with Claisen rearrangement or Claisen–Schmidt condensation. Claisen condensation Named after Rainer Ludwig Claisen Reaction type Condensation reaction Reaction R-COO-R′ + R-COO-R′ or Carbonyl + (Base: Na-OR') ↓ β-keto ester + R'-OH Conditions Typical solvents R'-OH Identifiers Organic Chemistry Portal claisen-condensation RSC ontology ID RXNO:0000043 The Claisen condensation is a carbon–carbon bond forming reaction that occurs between two esters...

 

India and the Non-Aligned Movement

Member and observer states of the Non-Aligned Movement (as of April 2022 ) For India, the concept of non-alignment began as a policy of non-participation in the military affairs of a bipolar world and in the context of colonialism aimed towards optimum involvement through multi-polar participation towards peace and security. It meant a country should be able to preserve a certain amount of freedom of action internationally. There was no set definition of non-alignment, which meant the term w...

Stato della materia

Questa voce o sezione sull'argomento fisica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sugli argomenti fisica e chimica è ritenuta da controllare. Motivo: Considerare i condensati di Bose-Einstein come uno stato principale, mentre molti altri analoghi non sono considerati ...

 

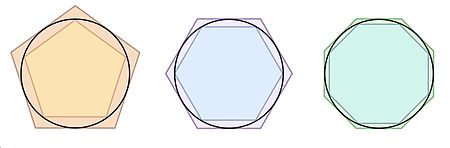
طريقة استنفاد

طريقة الاستنفاد (بالإنجليزية: Method of exhaustion)‏ هي طريقة لحساب مساحة شكل ما، عن طريق تأطير قيمة المساحة بمساحة مضلعات محيطة أو محاطة بالشكل.[1][2][3] عمليا، كلما كبر عدد الأضلاع، صار بالإمكان الاقتراب من المساحة الحقيقية أكثر. وبذلك يُحصل على تقريب لمساحة الشكل عندما...

 

Do You Remember

Do You RememberSingel oleh Jay Sean kolaborasi Sean Paul dan Lil Jondari album All or NothingDirilis3 November 2009Formatunduhan musik, CDDirekamSeptember 2009GenrePop, R&B, dance-popDurasi3:31LabelJayded, 2Point9 Records, Cash Money Records, Universal RepublicPenciptaJay Sean, Sean Paul, J remy (Jeremy Skaller & Robert Larow), Bobby Bass, Jared Cotter, Frankie Storm, & J PerkinsKronologi singel Down(2009) Do You Remember I Made It (Cash Money Heroes)(2010) Hold My Hand(2009) Do Y...

العلاقات الوسط إفريقية الدومينيكانية

العلاقات الوسط أفريقية الدومينيكانية جمهورية أفريقيا الوسطى جمهورية الدومينيكان   جمهورية أفريقيا الوسطى   جمهورية الدومينيكان تعديل مصدري - تعديل   العلاقات الوسط أفريقية الدومينيكانية هي العلاقات الثنائية التي تجمع بين جمهورية أفريقيا الوسطى وجمهورية ال...

 

Military of Champa

Military of the Kingdom of Champaꨣꨯꨢꩊ ꨌꩌꨛꨩ ꩌꨁꨤꨪꨓꨣꨳʾFounded192Disbanded1832Service branchesArmy Navy Provincial Armies and MilitiasLeadershipCommander-in-ChiefKing of ChampaRelated articlesHistoryMilitary History of Champa Champa Civil Wars Sino-Cham Wars Khmer-Cham wars Cham-Vietnamese Wars The military of Champa was the primary military force of Champa. The army and navy fought numerous wars and for defending their kingdom against the Chinese, Khmer and Vietna...

 

Lingaa

2014 film by K. S. Ravikumar For the representation of Shiva, see Lingam. For other uses of Linga, see Linga (disambiguation). LingaaTheatrical release posterDirected byK.S. RavikumarScreenplay byK.S. RavikumarStory byPon KumaranProduced byRockline VenkateshStarringRajinikanthK. ViswanathAnushka ShettySonakshi SinhaJagapathi BabuCinematographyR. RathnaveluEdited bySamjith MohammedMusic byA. R. RahmanProductioncompanyRockline Entertainments[1]Distributed byEros InternationalRelease dat...

Pyramide

Cet article concerne les pyramides en tant que polyèdres géométriques. Pour les autres significations, voir Pyramide (homonymie). Ensemble des pyramides Faces n {\displaystyle n} triangles,1 n-gone Arêtes 2 n {\displaystyle n} Sommets n {\displaystyle n} + 1 Groupe des isométries D2n Polyèdre dual Auto-duales Propriétés convexe En géométrie, une pyramide (du grec ancien πυραμίς / puramís) à n {\displaystyle n} côtés est un polyèdre à n {\displaystyle n} + 1 fa...

 

Fundamental group

Mathematical group of the homotopy classes of loops in a topological space For the fundamental group of a factor, see von Neumann algebra. In the mathematical field of algebraic topology, the fundamental group of a topological space is the group of the equivalence classes under homotopy of the loops contained in the space. It records information about the basic shape, or holes, of the topological space. The fundamental group is the first and simplest homotopy group. The fundamental group is a...