Banco de dados de gerenciamento de configuração
|
Read other articles:

Hominoïdes • Grands singes Hominoidea Un Humain (Hominidae) tenant un Gibbon à mains blanches (Hylobatidae), deux exemples d'hominoïdes.Classification MSW Règne Animalia Embranchement Chordata Classe Mammalia Ordre Primates Sous-ordre Haplorrhini Infra-ordre Simiiformes Micro-ordre Catarrhini Super-familleHominoideaGray, 1825 Familles de rang inférieur Hylobatidae (gibbons) Hominidae (orang-outans, gorilles, chimpanzés, bonobos et hommes) Les Hominoidea (Hominoïdes, ou grand...

Cinta Fitri Season 2Genre Drama Roman Keluarga PembuatMD EntertainmentDitulis olehHilman HariwijayaSkenarioHilman HariwijayaSutradaraEncep MasdukiPemeran Shireen Sungkar Teuku Wisnu Dinda Kanya Dewi Verlita Evelyn Iqbal Pakula Boy Tirayoh Irene Librawati Donita Adly Fairuz Fanny Ghassani Nuri Maulida Penggubah lagu temaRossaLagu pembukaAtas Nama Cinta oleh RossaLagu penutupAtas Nama Cinta oleh RossaPenata musikIwang ModulusNegara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim7Jmlh...

Giuseppe Verdi Fotografía de Giuseppe Verdi (ca. 1870), por Ferdinand Mulnier (1817-1891)Información personalNacimiento 10 de octubre de 1813 Le Roncole (Taro, Primer Imperio francés) Fallecimiento 27 de enero de 1901 Milán (Reino de Italia) Causa de muerte Accidente cerebrovascular Sepultura Casa Verdi FamiliaPadres Carlo Giuseppe y Luigia UttiniCónyuge Margherita Barezzi (1836-1840)Giuseppina Strepponi (1859-1897) Hijos Virginia Maria e Icilio RomanoEducaciónAlumno de Ferdin...

Election in Vermont Main article: 1900 United States presidential election 1900 United States presidential election in Vermont ← 1896 November 6, 1900 1904 → Nominee William McKinley William Jennings Bryan Party Republican Democratic Home state Ohio Nebraska Running mate Theodore Roosevelt Adlai E. Stevenson Electoral vote 4 0 Popular vote 42,569 12,849 Percentage 75.73% 22.86% County Results McKinley 60-70% 70-80% &#...

2007 family of multiprocessors by IBM This article's use of external links may not follow Wikipedia's policies or guidelines. Please improve this article by removing excessive or inappropriate external links, and converting useful links where appropriate into footnote references. (September 2017) (Learn how and when to remove this template message) POWER6Power6 CPUGeneral informationLaunched2007Designed byIBMPerformanceMax. CPU clock rate3.6 GHz to 5.0 GHzCacheL1 cache64+64 KB/coreL...

Pour un article plus général, voir Île de Pâques. L’histoire de l’île de Pâques comporte trois périodes : la période pré-anthropique : c’est l’histoire naturelle de l’île, depuis sa surrection en tant qu’ensemble volcanique il y a 750 000 ans aux marges de la plaque de Nazca, à la croisée de la dorsale est-Pacifique et de celle du Chili[1] et jusqu’à l’arrivée des premiers humains, en passant par la mise en place progressive de la flore (grai...

Italian mathematician Guido FubiniBorn(1879-01-19)19 January 1879VeniceDied6 June 1943(1943-06-06) (aged 64)New YorkAlma materScuola Normale Superiore di PisaKnown forFubini's theoremFubini's theorem on differentiationFubini–Study metricFubini numbersScientific careerFieldsMathematicsDoctoral advisorUlisse DiniLuigi Bianchi Guido Fubini[1] (19 January 1879 – 6 June 1943) was an Italian mathematician, known for Fubini's theorem and the Fubini–Study metric. Life Bor...

مزارع دينا الملعب ستاد السكة الحديد القاهرة البلد مصر الدوري تم تجميد النشاط الطقم الرسمي الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل نادي مزارع دينا نادي مصري لكرة القدم، كان اسمه في السابق نادي اتحاد عثمان لعب لعدة سنوات في الممتاز قبل الهبوط.[1][2][...

Long Island Rail Road branch Montauk BranchThe Cannonball runs express through Bay Shore to the Hamptons along the Montauk Branch.OverviewStatusOperationalOwnerLong Island Rail RoadLocaleLong Island, New York, USATerminiLong Island City (physical line); Babylon (service pattern)MontaukStations33 (physical line); 16 (service pattern)ServiceTypeCommuter rail, freight railSystemLong Island Rail RoadServices West Hempstead Branch Babylon Branch Montauk BranchOpe...

Pour les articles homonymes, voir D'Astros. Paul d'Astros Biographie Naissance 15 octobre 1772Tourves (France) Ordination sacerdotale 23 septembre 1797 par François d'Estienne Décès 29 septembre 1851 (à 78 ans)Toulouse (France) Cardinal de l'Église catholique Créécardinal 30 septembre 1850 par le pape Pie IX Titre cardinalice Cardinal-prêtre Évêque de l'Église catholique Ordination épiscopale 9 juillet 1820 par Hyacinthe-Louis de Quélen Archevêque métropolitainde Tou...

Kurau UtaraDesaKantor Desa Kurau Utara, Tanah LautPeta lokasi Desa Kurau UtaraNegara IndonesiaProvinsiKalimantan SelatanKabupatenTanah LautKecamatanBumi MakmurKode Kemendagri63.01.11.2002 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Kurau Utara adalah salah satu desa di Kecamatan Bumi Makmur, Tanah Laut, Kalimantan Selatan, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Adminis...

Province del Nepal Le province del Nepal (in nepalese: नेपालका प्रदेशहरू; Nepalka Pradeshaharu) sono state formate il 20 settembre 2015 in conformità all'allegato numero 4 della Costituzione del Nepal del 2015. Esse sono sette e sono state formate raggruppando i distretti già esistenti. Il sistema composto dalle sette province ha sostituito un sistema precedente secondo il quale il Nepal era diviso in 14 zone amministrative, che erano raggruppati in 5 regioni...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Ne doit pas être confondu avec Crespin. Crispin dans Recueil des modes de la cour de France par Nicolas Bonnart , circa 1678-1693 Crispin est un des plus célèbres personnages de théâtre des XVIIe et XVIIIe siècles. Personnage de l’ancienne comédie italienne apparu pour la première fois dans la pièce de Paul Scarron L’Écolier de Salamanque, Crispin, qui n’a rien de commun avec le poète ridicule de la satire latine, est de la famille de Scaramouche et il a dans le...

American author and lawyer Richard Henry Dana Jr.Dana, c. 1868United States Attorney for the District of MassachusettsIn office1861–1866PresidentAbraham LincolnPreceded byCharles L. WoodburySucceeded byGeorge Stillman Hillard Personal detailsBorn(1815-08-01)August 1, 1815Cambridge, Massachusetts, U.S.DiedJanuary 6, 1882(1882-01-06) (aged 66)Rome, Kingdom of ItalyPolitical partyFree SoilRepublicanOther politicalaffiliationsIndependent Republican (1868)Signature Richard Henry Dana ...

1991 video gameDeath Knights of KrynnCover art is based on the painting Lord Soth's Charge by Keith Parkinson.[1]Developer(s)Strategic SimulationsPublisher(s)Strategic SimulationsDirector(s)Victor PenmanDesigner(s)Ken HumphriesDave ShelleyArtist(s)Tom WahlWriter(s)Dave GovettComposer(s)George Alistair SangerDavid GovettSeriesGold BoxPlatform(s)Amiga, C64, MS-DOS, NEC PC-9801Release1991Genre(s)Role-playing video game, tactical RPGMode(s)Single-player Death Knights of Krynn is the secon...
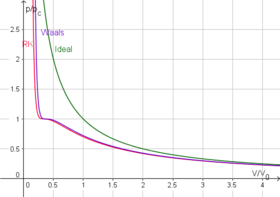
Non-hypothetical gases whose molecules occupy space and have interactions ThermodynamicsThe classical Carnot heat engine Branches Classical Statistical Chemical Quantum thermodynamics Equilibrium / Non-equilibrium Laws Zeroth First Second Third Systems Closed system Open system Isolated system State Equation of state Ideal gas Real gas State of matter Phase (matter) Equilibrium Control volume Instruments Processes Isobaric Isochoric Isothermal Adiabatic Isentropic Isenthalpic Quasist...

城市故事City Japes类型處境喜劇主演溫兆倫、曾近榮、丁 茵、何美婷、梁思浩、郭晉安、羅嘉良、劉淑華、唐麗球、何偉龍、彭健新、吳茜薇集数455主题曲Plucky Fella [1]作曲David Snell制作拍摄/制作年份1986年-1988年制作统筹黃 令、郭靜霞监制梁材遠编审岑國榮、韋家輝、余詠珊、鄧特希拍攝地點 英屬香港制作公司香港電視廣播有限公司無綫電視翡翠台首播 播出日�...

X-Men Ficha técnicaDirección Bryan SingerProducción Lauren Shuler DonnerRalph Winter Richard Donner (Productor ejecutivo)Guion David HayterHistoria Bryan SingerTom DeSantoBasada en X-Men porJack Kirby y Stan LeeMúsica Michael KamenFotografía Newton Thomas SigelMontaje Steven RosenblumJohn WrightKevin StittVestuario Louise MingenbachNarrador Patrick StewartProtagonistas Patrick Stewart Hugh Jackman Ian McKellenHalle BerryFamke JanssenJames Marsden Bruce DavisonRebecca RomijnRay ParkTyler ...