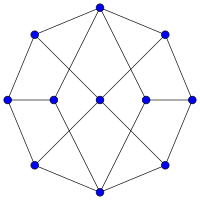
Ścieżka Hamiltona
|
Read other articles:

Untuk kegunaan lain, lihat Api Suci (disambiguasi). Mukjizat Api Suci, karya William Holman Hunt Api Suci (Bahasa Yunani Ἃγιον Φῶς, Sinar Suci) dideskripsikan oleh umat Kristen Ortodoks sebagai sebuah mukjizat yang terjadi setiap tahun di Gereja Makam Kudus, Yerusalem, pada Sabtu Agung, atau Sabtu Suci, sehari sebelum Paskah Kristen Ortodoks. Deskripsi dalam iman Ortodoks Tradisi Ortodoks menyatakan bahwa Api Suci terjadi setiap tahun pada sehari sebelum Paskah Ortodoks, di mana sin...

This is a list of notable quarries and areas of quarrying in the United States. A number of these are historic quarries listed on the National Register of Historic Places (NRHP), ranging from relatively ancient archeological sites to places having pre-World War II activity. This includes major areas of continuing, modern quarrying. According to Marble.com, in 2016 there were 276 quarries producing natural stone in 34 states, and states producing the most granite were Texas, Massachusetts, In...

Daging ham Ham adalah bagian daging babi yang berasal dari bagian kaki belakang. Ham dibuat di seluruh dunia, termasuk beberapa makanan khas daerah, meskipun istilah ini memiliki penggunaan yang lebih luas dan dapat digunakan untuk merujuk pada daging babi yang telah dibentuk kembali. Selain itu, ada banyak memiliki produk perlindungan ham secara geografis, seperti Prosciutto di Parma di Eropa, dan Smithfield ham di Amerika Serikat. Merek yang dilindungi Belgia Jambon d'Ardenne - Wallonia, Be...
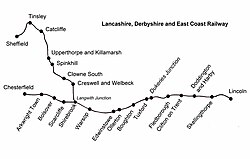
This article is about the Boughton station in Nottinghamshire. For the Northamptonshire station, see Boughton railway station. Former railway station in Nottinghamshire, England Boughton (Notts)The site of the former stationGeneral informationLocationBoughton, Newark and Sherwood, NottinghamshireEnglandGrid referenceSK 688 678Platforms2Other informationStatusDisusedHistoryOriginal companyLD&ECRPre-groupingGreat Central RailwayPost-groupingLNERBritish RailwaysKey dates8 March 1897Opened19 ...

العلاقات الأندورية الزامبية أندورا زامبيا أندورا زامبيا تعديل مصدري - تعديل العلاقات الأندورية الزامبية هي العلاقات الثنائية التي تجمع بين أندورا وزامبيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة أ�...

دولار ليبيري5 دولار ليبيريةمعلومات عامةالبلد ليبيريا المنطقة ليبيريا رمز العملة Lib$L$ رمز الأيزو 4217 LRD المصرف المركزي البنك المركزي الليبيري سعر الصرف 0٫005429 يورو (3 فبراير 2019) العملات المعدنية 5، 10، 25، 50، سنت، دولار واحد[1]تعديل - تعديل مصدري - تعديل ويكي بيانات الدولار الل�...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

Fundamental law of Estonia Politics of Estonia State Constitution Declaration of Independence Human rights Presidency President Alar Karis Executive Prime Minister Kaja Kallas Government of Estonia Incumbent cabinet Legislature Riigikogu Speaker: Lauri Hussar Judiciary Supreme Court Chancellor of Justice Elections Political parties Recent elections Riigikogu:201520192023 Presidential:201120162021 Municipal: 200920132017 European: 201420192024 Administrative divisions Counties Municipalities F...

L'énergie des vagues, ou énergie houlomotrice, est une énergie marine utilisant l'énergie contenue dans le mouvement de la houle, soit les oscillations de la surface de l'eau. Cette énergie ne doit pas être confondue avec l'énergie marémotrice, laquelle utilise l'énergie des marées[1]. La faisabilité de son exploitation a été étudiée, en particulier au Portugal, au Royaume-Uni et en Australie. Histoire La première utilisation de l'énergie des vagues fut probablement un systè...

Multi-sport event in Sarajevo, Yugoslavia XIV Olympic Winter GamesLogo of the 1984 Winter Olympics[a]Host citySarajevo, Yugoslavia (now in Bosnia and Herzegovina)Nations49Athletes1,272 (998 men, 274 women)Events39 in 6 sports (10 disciplines)Opening8 February 1984Closing19 February 1984Opened byPresident of the Presidency Mika ŠpiljakCauldronSanda DubravčićStadiumKoševo StadiumWinter← Lake Placid 1980Calgary 1988 → Summer← Moscow 1980Los Angeles 19...

Place in Alexandria, EgyptSan Stefano San Stefano سان ستفانوSan StefanoLocation in EgyptCoordinates: 31°14′48″N 29°58′12″E / 31.246709°N 29.969916°E / 31.246709; 29.969916Country EgyptGovernorateAlexandriaCityAlexandriaTime zoneUTC+2 (EST) San Stefano (Egyptian Arabic: سان ستفانو) is a neighborhood in Alexandria, Egypt. The area was known for a landmark hotel-casino that was demolished in the late 1990s. That hotel was replaced by the...

Coppa Europa di sci alpino 1991 Uomini Donne Vincitori Generale Tobias Barnerssoi Markus Eberle Alexandra Meissnitzer Discesa libera Christophe Plé Gabriele Papp Supergigante Jérôme Noviant Alexandra Meissnitzer Slalom gigante Tobias Barnerssoi Alexandra Meissnitzer Slalom speciale Dietmar Thöni Annelise Coberger 1990 1992 La Coppa Europa di sci alpino 1991 fu la 20ª edizione della manifestazione organizzata dalla Federazione Internazionale Sci. In campo maschile il tedesco Tobias Barne...

「伊斯兰国家」重定向至此。關於一种政权形式,請見「伊斯兰国 (政权形式)」。 此條目需要补充更多来源。 (2019年2月22日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:穆斯林世界 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的...

Pour les articles homonymes, voir Bellen. Alexander Van der Bellen Alexander Van der Bellen en 2021. Fonctions Président fédéral d'Autriche En fonction depuis le 26 janvier 2017(7 ans, 3 mois et 16 jours) Élection 4 décembre 2016 Réélection 9 octobre 2022 Chancelier Christian KernSebastian KurzHartwig Löger (intérim)Brigitte BierleinSebastian KurzAlexander SchallenbergKarl Nehammer Prédécesseur Intérim collégialHeinz Fischer Porte-parole fédéral des Verts 13 dé...

El Salvador en los Juegos Paralímpicos Bandera de El SalvadorCódigo CPI ESACPN Comité Paralímpico de El SalvadorJuegos Paralímpicos de Londres 2012Deportistas 1Medallas 0 0 0 0 Historia paralímpicaJuegos de verano 2000 • 2004 • 2008 • 2012 • 2016 • 2020 •[editar datos en Wikidata] El Salvador estuvo representado en los Juegos Paralímpicos de Londres 2012 por un deportista masculino.[1] El equipo paralím...

Member of the British royal family KatharineDuchess of Kent (more)Katharine (holding a koala) in 1988BornKatharine Lucy Mary Worsley (1933-02-22) 22 February 1933 (age 91)Hovingham Hall, Yorkshire, EnglandSpouse Prince Edward, Duke of Kent (m. 1961)Issue George Windsor, Earl of St Andrews Lady Helen Taylor Lord Nicholas Windsor HouseWorsleyFatherSir William Worsley, 4th BaronetMotherJoyce BrunnerReligionRoman Catholicprev. AnglicanSignatureEducation...

Audio recording using magnetic tape spooled on open reels Reel to reel redirects here. For other uses, see Reel to reel (disambiguation). A reel-to-reel tape recorder (Sony TC-630), typical of a 1970s audiophile device. Reel-to-reel audio tape recording, also called open-reel recording, is magnetic tape audio recording in which the recording tape is spooled between reels. To prepare for use, the supply reel (or feed reel) containing the tape is placed on a spindle or hub. The end of the tape ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أغسطس 2019) النسخة الخامسة من الأفروآسيوية بين النادي الإفريقي التونسي والهلال السعودي وفاز النادي الإفريقي. الكأس ا...

Internationale de l'éducationHistoireFondation 26 janvier 1993Prédécesseurs Secrétariat professionnel international de l'enseignement (en), Confédération mondiale des organisations de la profession enseignante (en), Confédération syndicale mondiale de l'enseignement (en)CadreType Fédération syndicale internationaleDomaine d'activité ÉducationOrganisationSite web www.ei-ie.org/frmodifier - modifier le code - modifier Wikidata L'Internationale de l’éducation (IE) est une organisa...