Widmowa gęstość mocy
|
Read other articles:

Dr. Drs. Ir. H.Achmad TarmiziS.E., S.H., S.T., M.T., M.Si., M.H., M.Pd., Ph.D.(H.C.) Sekretaris Daerah Ogan Komering UluPetahanaMulai menjabat 27 Desember 2017PresidenJoko Widodo PendahuluUmirtomMarwan SobriePenggantiPetahanaPresidenSusilo Bambang Yudhoyono Joko WidodoGubernurAlex Noerdin Herman Deru Informasi pribadiLahir09 Juni 1966 (umur 57) Palembang, Sumatera SelatanKebangsaan IndonesiaSuami/istriHj. Susmadiana, S.Pd., S.Mn., M.Si., M.Pd.HubunganAl Farrel Atharizz Calief Ad...

Perdana Menteri Jang Bahadur Rana Maharaja Jung Bahadur Rana (bahasa Nepali: जंग बहादुर राणा) (atau Jang Bahadur Kunwar (bahasa Nepali: जंग बहादुर कुँवर), GCB, GCSI, 18 Juni 1816 – 25 Februari 1877) adalah perdana menteri, penguasa Nepal dan pendiri dinasti Rana di Nepal. Nama aslinya adalah Bir Narsingh Kunwar namun dia menjadi terkenal dengan nama Jang Bahadur, yang diberikan kepadanya oleh Mathebar Thapa, paman d...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Boston Braves AHL – news · newspapers · books · scholar · JSTOR (September 2012) This articl...

Racism debate in American football Main article: Native American mascot controversy Part of a series onDiscrimination Forms Institutional Structural Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti...

Bambang HermantoS.E. Anggota Dewan Perwakilan Rakyat Republik IndonesiaPetahanaMulai menjabat 7 Desember 2020PresidenJoko WidodoPendahuluDaniel Mutaqien SyafiuddinPenggantiPetahanaDaerah pemilihanJawa Barat VIII Informasi pribadiLahir14 September 1976 (umur 47)Indramayu, Jawa BaratPartai politikGolkarSuami/istriNurkomalaAnak4Alma materUniversitas Padjadjaran Universitas JayabayaSunting kotak info • L • B Bambang Hermanto, S.E. (lahir 14 September 1976) adalah politikus ...
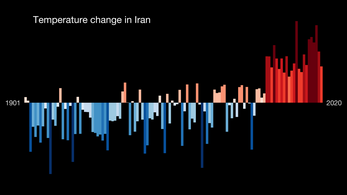
Emissions, impacts and responses in Iran related to climate changeLake Urmia has shrunk due to reduced inflow in recent decades. This is attributable to climate change, and contributes to water scarcity in Iran.[1] Iran is among the most vulnerable countries to climate change in the Middle East and North Africa (MENA). Iran contributes to about 1.8% of global greenhouse gas emissions (GHG), and is ranked 8th in greenhouse gas emissions (GHG) world wide and is ranked first in the MENA ...

American racing driver (born 1994) NASCAR driver Chase BriscoeBriscoe at Las Vegas Motor Speedway in 2024BornChase David Wayne Briscoe (1994-12-15) December 15, 1994 (age 29)Mitchell, Indiana, U.S.Height6 ft 1 in (1.85 m)Achievements2016 ARCA Racing Series Champion2020 Carolina Midget Showdown WinnerAwards2016 Bill France Four Crown2017 NASCAR Camping World Truck Series Rookie of the Year2017 NASCAR Camping World Truck Series Most Popular Driver2019 NASCAR Xfinity Series R...

American politician This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Ronald N...

2019 American filmInvader Zim: Enter the FlorpusPromotional release posterDirected by Hae Young Jung Young Kyun Park Jhonen Vasquez Written byJhonen VasquezBased onInvader Zimby Jhonen VasquezProduced byJoann EstoestaStarring Richard Steven Horvitz Rosearik Rikki Simons Andy Berman Melissa Fahn Rodger Bumpass Edited byJonathan SimsMusic byKevin MantheiProductioncompanyNickelodeon Animation StudioDistributed byNetflixRelease date August 16, 2019 (2019-08-16) Running time71 minu...

Contact sport on roller skates For the skate brand of the same name, see Roller Derby (brand). Roller derbyA roller derby scrimmage in Utah (2012)Highest governing bodyWFTDA, MRDA, JRDA, FIRSNicknamesDerbyFirst played1935, Chicago, IllinoisClubs4,700+CharacteristicsContactFullTeam members15 on roster, up to 5 on track during each jam.[1]TypeIndoor, roller sportEquipmentRoller skates, helmet, knee pads, elbow pads, wrist guards, mouthguardVenueRoller rink, pitchPresenceOlympicNo R...

Final Piala FA 1952TurnamenPiala FA 1951–1952 Newcastle United Arsenal 1 0 Tanggal3 Mei 1952StadionStadion Wembley, LondonWasitArthur EllisPenonton100.000← 1951 1953 → Final Piala FA 1952 adalah pertandingan sepak bola antara Newcastle United dan Arsenal yang diselenggarakan pada 3 Mei 1952 di Stadion Wembley, London. Pertandingan ini merupakan pertandingan final ke-71 Piala FA sebagai pertandingan penentu pemenang musim 1951–1952. Pertandingan ini dimenangkan oleh Newcastle U...

Disambiguazione – Corneille rimanda qui. Se stai cercando altri significati, vedi Corneille (disambigua). Pierre Corneille Pierre Corneille (Rouen, 6 giugno 1606 – Parigi, 1º ottobre 1684) è stato un drammaturgo e scrittore francese, uno dei tre maggiori del XVII secolo, insieme a Molière e Racine. Indice 1 Biografia 1.1 Gli esordi (la commedia) 1.2 Le tragedie 1.2.1 Il Cid 1.3 Gli ultimi anni: declino e morte 1.4 Temi del teatro di Corneille 2 Opere principali 3 Note 4 Biblio...

British actress and singer Klariza ClaytonBorn (1989-03-09) 9 March 1989 (age 35)British Hong KongOccupationActressYears active2007–present Klariza L. Clayton (born 9 March 1989) is a British actress and singer. She is best known for her roles in the CBBC comedy Dani's House (2008–2012), the E4 drama Skins (2009–2010), the Nickelodeon series House of Anubis (2011–2013),[1][2] and the Netflix sitcom Lovesick (2016–2018). Early life Clayton was born in Hong K...

تبجيل في نوتو القديس كونراد من بياتشنزا (سان كورادو) تبجيل (لغة لاتينية veneratio، لغة يونانية δουλεία، douleia)، أو تبجيل القديسين، هو عمل خاص لتكريم القديس، وهوالشخص الذي يتميز بامتلاكه قدرًا كبيرًا من القدسية أو القداسة.[1] وتحظى الملائكة بتبجيلٍ مماثل في العديد من الديانات....

Ocean boundary current that flows along the coast of Somalia and Oman in the Western Indian Ocean The Somali Current off the Somali coast in the context of the Indian Ocean Gyre during (northern) summer. The circular current east of the Horn of Africa is known as the Great Whirl The Somali Current is a warm ocean boundary current that runs along the coast of Somalia and Oman in the Western Indian Ocean and is analogous to the Gulf Stream in the Atlantic Ocean.[1] This current is heavi...

Flag of the Brazilian state of Pará State of ParáUseCivil and state flag Proportion7:10[1]Adopted3 June 1890[2]DesignIn the field of sips (red) a silver band (white), carried in the center of a blau star (blue). The flag of the state of Pará is, along with the coat of arms and the anthem, one of the symbols of the state of Pará, Brazil as described in article 12 of the state constitution.[3] History One day after joining the nation of Brazil on November 16, 1889, a...

Bharatnatyam dancer from Delhi, India Geeta ChandranBornDelhi, IndiaKnown forDancer - BharatanatyamSpouseRajiv Chandran (married 1985-present)AwardsPadma Shri Geeta Chandran is an Indian Bharatanatyam dancer and vocalist.[1][2] Trained in Carnatic music, she is a visionary and celebrated artist in Indian classical Bharatanatyam, recognized for her work in theatre, dance, education, videos and films.[3] Career In order to expand her frontiers in the classical arts,...

金丸駅 駅舎(2020年7月) かねまる Kanemaru ◄千路 (3.7 km) (3.6 km) 能登部► 所在地 石川県鹿島郡中能登町金丸又れ49北緯36度56分36.55秒 東経136度50分10.70秒 / 北緯36.9434861度 東経136.8363056度 / 36.9434861; 136.8363056座標: 北緯36度56分36.55秒 東経136度50分10.70秒 / 北緯36.9434861度 東経136.8363056度 / 36.9434861; 136.8363056所属事業者 西日本旅客鉄...

American art historian Allan MarquandBorn(1853-12-10)December 10, 1853New York City, New York, U.S.DiedSeptember 24, 1924(1924-09-24) (aged 70)New York City, New York, U.S.Alma materSt. Paul's School (New Hampshire)Princeton UniversityJohns Hopkins UniversityOccupationArt historianKnown forCurator of the Princeton University Art MuseumSpouse Eleanor Cross (m. 1896)ChildrenEleanor Marquand DelanoyMary Marquand HochschildSarnia MarquandAllan Marquan...

Part of a series onSpacetime Special relativity General relativity Spacetime concepts Spacetime manifold Equivalence principle Lorentz transformations Minkowski space General relativity Introduction to general relativity Mathematics of general relativity Einstein field equations Classical gravity Introduction to gravitation Newton's law of universal gravitation Relevant mathematics Four-vector Derivations of relativity Spacetime diagrams Differential geometry Curved space Curved spacetime Mat...






















![{\displaystyle E\left[{\frac {|{\mathcal {F}}(f_{T}(t))|^{2}}{T}}\right]\to S(f).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47dd0c925ca7897e357a39caa826aef10ba2de1c)

















