Skręcanie
|
Read other articles:

Sporting event delegationGermany at the2016 Summer ParalympicsIPC codeGERNPCNational Paralympic Committee GermanyWebsitewww.dbs-npc.de (in German)in Rio de JaneiroCompetitors155[1] in 14 sportsMedalsRanked 6th Gold 18 Silver 25 Bronze 14 Total 57 Summer Paralympics appearances (overview)19601964196819721976198019841988199219962000200420082012201620202024Other related appearances East Germany (1984) Germany competed at the 2016 Summer Paralympics in Rio de Janeiro, Brazil, fr...

Ronald George Wreyford NorrishYayasan Nobel, 1967Lahir(1897-11-09)9 November 1897Cambridge, United KingdomMeninggal7 Juni 1978(1978-06-07) (umur 80)Cambridge, United KingdomKebangsaanUnited KingdomAlmamaterCambridge UniversityDikenal atasReaksi NorrishPenghargaanPenghargaan Nobel Kimia (1967)Royal Society[1] Medali Davy (1958)Karier ilmiahBidangKimiaInstitusiCambridge UniversityPembimbing doktoralEric Keightley Rideal Ronald George Wreyford Norrish (9 November 1897 – 7 Juni 19...
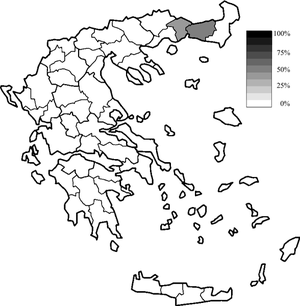
Peta prefektur-prefetur Yunani menurut sensus tahun 1991 yang menunjukkan persentase minoritas Muslim di Trakia Barat. Minoritas Muslim di Yunani adalah satu-satunya kelompok minoritas yang diakui secara resmi di Yunani. Kelompok ini berjumlah 97.605 jiwa (0,91% populasi) menurut sensus tahun 1991,[1] dan 140.000 people atau 1,24% populasi menurut Departemen Dalam Negeri Amerika Serikat.[2] Seperti wilayah Balkan selatan lainnya yang dikuasai oleh Kesultanan Utsmaniyah selama ...

Sommières-du-ClaincomuneSommières-du-Clain – Veduta LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Vienne ArrondissementMontmorillon CantoneCivray TerritorioCoordinate46°17′N 0°21′E / 46.283333°N 0.35°E46.283333; 0.35 (Sommières-du-Clain)Coordinate: 46°17′N 0°21′E / 46.283333°N 0.35°E46.283333; 0.35 (Sommières-du-Clain) Superficie26,46 km² Abitanti819[1] (2009) Densità30,95 ab./km² Altre ...

Untuk PTRI yang mewakili kepentingan Indonesia pada organisasi PBB di Jenewa, lihat Perutusan Tetap Indonesia untuk Perserikatan Bangsa-Bangsa, Organisasi Perdagangan Dunia, dan Organisasi Internasional Lainnya di Jenewa. Perutusan Tetap Republik Indonesia untuk Perserikatan Bangsa-Bangsa di New YorkPermanent Mission of the Republic of Indonesia to the United Nations, New YorkLokasi Kota New York, Amerika SerikatAlamat325 East 38th Street, New York, NY, 10016, USADuta BesarArrmanatha Chris...

Kenyan marathon runner Barno had a time of 2:11:58 in his 2018 win of the Twin Cities Marathon.[1] Elisha Kiprop Barno (born 1985) is a Kenyan marathon runner. Barno is the most prolific runner in Grandma's Marathon history, winning the race five times 2015 to 2018 and again in 2023.[2] He has won several marathons during his career, including the Los Angeles Marathon,[3] the Jacksonville Marathon, and the California International Marathon. His best time is 2:09:14, in...

格奥尔基·马林科夫Гео́ргий Маленко́в苏联共产党中央书记处书记(排名第一)任期1953年3月5日—1953年3月13日前任约瑟夫·斯大林继任尼基塔·赫鲁晓夫(第一书记)苏联部长会议主席任期1953年3月5日—1955年2月8日前任约瑟夫·斯大林继任尼古拉·布尔加宁 个人资料出生1902年1月8日[儒略曆1901年12月26日] 俄罗斯帝国奥伦堡逝世1988年1月14日(1988歲—01—14)(86歲)&#...

Cet article est une ébauche concernant l’histoire, une personnalité suédoise et la monarchie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Estelle de Suède La princesse Estelle en 2023. Biographie Titulature Princesse de SuèdeDuchesse d'Östergötland Dynastie Maison Bernadotte Distinctions Ordre des Séraphins Nom de naissance Estelle Silvia Ewa Mary Bernadotte Naissance 23 février 2012 (12 ans)...

عبد الرؤوف بن غيت معلومات شخصية الميلاد 5 أبريل 1996 (العمر 28 سنة)الأغواط الطول 1.70 م (5 قدم 7 بوصة) مركز اللعب ظهير [لغات أخرى] الجنسية الجزائر معلومات النادي النادي الحالي الرجاء الرياضي مسيرة الشباب سنوات فريق 2008–2013 بارادو المسيرة الاحترافية1 سنوا�...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Marginalisation redirects here. For the concept in probability, see Marginal distribution. Form of social disadvantage and relegation to the fringe of society This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (July 2016) (Learn how and when to remove this message) Part of a series onCommunit...

Branch of chemistry Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems.[1] It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of molecules, groups of molecules, and solids.[2] The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion (dihydrogen cation)...

Practice of trading financial instruments using a firm's own money This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Proprietary trading – news · newspapers · books · scholar · JSTOR (December 2020) (Learn how and when to remove this message) Proprietary trading (also known as prop trading) occurs when a trade...

Concept in philosophy and psychology This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (August 2022) (Learn how and when to remove this message) The founder of phenomenology, Edmund Husserl, identified the Other as one of the conceptual bases of intersubjectivity, of the relations among people. Other is a term used to define another person or people as separate from oneself...

ميّز عن قسطنطين السادس من القسطنطينية. قسطنطين السادس Constantine VI Constantine VI (right to the cross) presiding over the مجمع نيقية الثاني. Miniature from early 11th century. قائمة الأباطرة البيزنطيين الذين حكموا الإمبراطورية البيزنطية فترة الحكم8 سبتمبر 780– أغسطس 797 معلومات شخصية الميلاد 771القسطنطينية ا�...

Bader Al-Mutawa Informasi pribadiTanggal lahir 5 Januari 1985 (umur 39)Tempat lahir Kuwait City, KuwaitTinggi 1,75 m (5 ft 9 in)Posisi bermain ForwardInformasi klubKlub saat ini QadsiaNomor 17Karier senior*Tahun Tim Tampil (Gol)2002– Qadsia 254 (202)2007 → Qatar SC (loan) 1 (0)2011 → Al Nassr (loan) 9 (13)Tim nasional‡2003– Kuwait 156 (51) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik dan akurat per 20 January 2016‡ Penampilan dan ...

Time that it takes to complete one rotation relative to the background stars Rotation period redirects here. For the general concept, see Rotation period (physics). Earth's rotation imaged by Deep Space Climate Observatory, with axis tilt In astronomy, the rotation period or spin period[1] of a celestial object (e.g., star, planet, moon, asteroid) has two definitions. The first one corresponds to the sidereal rotation period (or sidereal day), i.e., the time that the object takes to c...

Questa voce o sezione sull'argomento mitologia romana non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. La Lupa senese in piazza Duomo I gemelli Senio (o Seno) e Ascanio (o Aschio) erano, secondo la leggenda altomedievale senese, i figli di Remo, gemello di Romolo. La leggenda vuole che i due fratelli siano...

Возможно, эта статья содержит оригинальное исследование. Проверьте соответствие информации приведённым источникам и удалите или исправьте информацию, являющуюся оригинальным исследованием. В случае необходимости подтвердите информацию авторитетными источниками. В �...

كارلوس دييغو فيريرا معلومات شخصية الميلاد 18 يناير 1985 (39 سنة)[1][2] مواطنة البرازيل الحياة العملية المهنة مُقاتل فنون قتالية مختلطة[3] اللغات البرتغالية الرياضة فنون القتال المختلطة[3] المواقع IMDB صفحته على IMDB تعديل مصدري - تعديل كارلوس د...
![{\displaystyle q=[0;q_{vy};q_{vz}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13751fa7f4c00424eff553597ea5e470bbb73f3e)











![{\displaystyle {\vec {u}}=[u;v;w]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29833c12e2926a9a6e97f32e30db6e939af3b3a7)



























