Vinkelens tredeling
|
Read other articles:

Science fiction subgenre in a futuristic dystopian setting For other uses, see Cyberpunk (disambiguation). Artificial landscapes and city lights at night were some of the first metaphors used by the genre for cyberspace (in Neuromancer, by William Gibson). From top to bottom: Shibuya, Tokyo (Japan), Times Square, New York (United States), Monterrey, Nuevo León (Mexico) and São Paulo (Brazil). Cyberpunk is a subgenre of science fiction in a dystopian futuristic setting that tends to focus on...
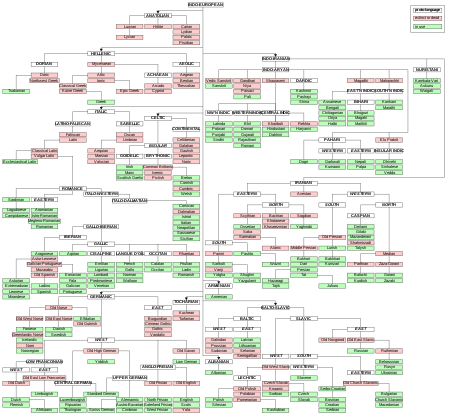
Ancestor of the Indo-European languages PIE and Proto-Indo-European redirect here. For the people, see Proto-Indo-Europeans. For other uses, see PIE (disambiguation). Not to be confused with Pre-Indo-European languages or Paleo-European languages. Proto-Indo-EuropeanPIEReconstruction ofIndo-European languagesRegionPontic–Caspian steppe (Proto-Indo-European homeland)Erac. 4500 – c. 2500 BCLower-order reconstructions Proto-Albanian Proto-Anatolian Proto-Armenian Proto-...

منتخب السعودية تحت 20 سنة لكرة القدم معلومات عامة بلد الرياضة السعودية الفئة كرة قدم تحت 20 سنة للرجال [لغات أخرى] رمز الفيفا KSA الاتحاد اتحاد السعودية لكرة القدم كونفدرالية الاتحاد الآسيوي لكرة القدم الملعب الرئيسي ملعب الملك فهد الدولي الطاقم واللاعبون...

Belgian cyclist (born 1945) For the bicycle brand, see Eddy Merckx Cycles. For the billiards player, see Eddy Merckx (billiards player). Eddy MerckxMerckx in 1971Personal informationFull nameÉdouard Louis Joseph MerckxNicknameLe Cannibale De Kannibaal (The Cannibal)[1]Born (1945-06-17) 17 June 1945 (age 78)Meensel-Kiezegem, BelgiumHeight1.82 m (5 ft 11+1⁄2 in)[2]Weight74 kg (163 lb; 11 st 9 lb)[2]Team informationCurre...

Nomenclatura della volta a botte: (1) chiave di volta; (2) cuneo; (3) estradosso; (4) piedritto; (5) intradosso; (6) freccia; (7) corda; (8) rifinanziamento o rinfianco. La volta a botte è una semi circonferenza ed è tra i sistemi più semplici di copertura non piana, utilizzata per coprire spazi di forma genericamente rettangolare. Due volte a botte, che si intersecano perpendicolarmente, formano la volta a crociera. Indice 1 Aspetti costruttivi 2 Aspetti geometrici 3 Tipologie 4 Esempi di...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

35°12′N 3°55′W / 35.200°N 3.917°W / 35.200; -3.917 الريف الريف 1921م – 1926 جمهورية الريفعلم جمهورية الريفشعار ملف:Territorio de la República del Rif (1921-1926).png عاصمة أجدير نظام الحكم جمهورية اللغة الرسمية الريفية اللغة العربية لهجة جبلية والأمازيغية لهجة تاريفيت الرئيس محمد عبد الكريم ا...

Trend Building, Universitas Nottingham Ningbo Tiongkok Universitas Nottingham Ningbo Tiongkok (Hanzi: 宁波诺丁汉大学 Pinyin: ningbo nuodinghan daxue) adalah sebuah kampus dari Universitas Nottingham (Britania Raya) yang terletak di kota Ningbo, Zhejiang, dekat kota Shanghai. Universitas ini merupakan universitas pertama kerja sama negara Tiongkok dan negara lain. Universitas Nottingham Ningbo Tiongkok terletak di Taman Pendidikan Tinggi Ningbo. Universitas yang merupakan buah hasil ker...

For related races, see 2000 United States gubernatorial elections. 2000 Vermont gubernatorial election ← 1998 November 7, 2000 2002 → Nominee Howard Dean Ruth Dwyer Anthony Pollina Party Democratic Republican Progressive Popular vote 148,059 111,359 28,116 Percentage 50.5% 38.0% 9.6% County results Municipality resultsDean: 30-40% 40-50% 50-60% &...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (ديسمبر 2018) مقاطعة مونو الإحداثيات 37°55′00″N 118°52′00″W / 37.916666666667°N 118.86666666667...

Neolithic archaeological site in Turkey Karahan TepeKarahan TepeShown within TurkeyShow map of TurkeyKarahan Tepe (Near East)Show map of Near EastKarahan Tepe (Eastern Mediterranean)Show map of Eastern MediterraneanLocationKarahan Tepe, Şanlıurfa Province, TurkeyCoordinates37°05′33″N 39°18′13″E / 37.09250°N 39.30361°E / 37.09250; 39.30361HistoryPeriodsPre-Pottery Neolithic A to B Karahan Tepe (Kurdish: Girê Keçel)[1][2] is an archaeologi...

「人民民主阵线」重定向至此。关于中非共和国的同名政党,请见「人民民主阵线 (中非共和国)」。 人民民主黨人民民主黨标志英語名称People's Democratic Party召集人賴宗育[1]创始人鄭村棋成立2011年10月2日总部 中華民國新北市三重區光明路32巷33號党员無黨員制度意識形態社會主義[2]政治立場左翼[3]国际组织無立法委員0 / 113直轄市長0 / 6直轄市議...

Hinduism by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Morocco Western Sahara Mozambique Namibia Niger Nigeria Rwanda São Tomé and Príncipe Senegal Seychelles Sierra Leone Som...

Upper house of Algerian Parliament Council of the Nation مجلس الأمةTypeTypeUpper house of the Parliament of Algeria HistoryFounded1997LeadershipPresidentSalah Goudjil, RND since 9 April 2019 Vice presidentDjamel Ould Abbes, FLN since 28 February 2019 StructureSeats174 membersPolitical groupsGovernment (147) FLN (54) RND (22) FM (7) Binaa (7) TAJ (7) Appointed Members (58) Opposition (9) FFS (4) PVP (2) El Fadjr El...

2013 Bangladeshi presidential election ← 2009 22 April 2013 2018 → Nominee Abdul Hamid Party AL Electoral vote Unopposed President before election Abdul Hamid (acting) AL Elected President Abdul Hamid AL This article is part of a series on thePolitics of Bangladesh Constitution Amendments Law of Bangladesh Bangladesh Code Penal Code Human rights Article 70 Judicial review Government President: Mohammed Shahabuddin Prime Minister: Sheikh Hasina Cabinet: Hasina...

Motorcycle This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Royal Enfield Bullet – news · newspapers · books · scholar · JSTOR (August 2010) (Learn how and when to remove this message) Type of motorcycle Royal Enfield BulletManufacturerRoyal Enfield, UK (1931–1966)Royal Enfield, India (1955–present)Produc...

Palma de Mallorca Palma Municipio y ciudad de EspañaBanderaEscudo De izquierda a derecha y de arriba abajo: una panorámica de la ciudad, el castillo de Bellver, el Palacio Real de La Almudaina, la playa de Can Pere Antoni, la Plaza Mayor y la Catedral de Santa María de Palma de Mallorca. Palma de MallorcaUbicación de Palma de Mallorca en España Palma de MallorcaUbicación de Palma de Mallorca en las Islas Baleares Mapa interactivoPaís España• Com. autónoma ...

Taça de PortugalSport Calcio TipoClub Paese Portogallo OrganizzatoreFederazione calcistica del Portogallo CadenzaAnnuale Aperturaagosto Chiusuramaggio Partecipanti172 FormulaEliminazione diretta Sito InternetSito ufficiale StoriaFondazione1938 Detentore Porto Record vittorie Benfica (26) Ultima edizioneTaça de Portugal 2023-2024 Trofeo o riconoscimento Modifica dati su Wikidata · Manuale La Taça de Portugal, nota in italiano come Coppa di Portogallo, è una competizion...

An equestrian seal is a type of seal used in the European Middle Ages, characterized by the depiction of the owner as a mounted warrior in full armour. Originating in the high medieval period (late 11th to early 12th century), the type was frequently used throughout the 13th to 14th centuries. Continued use into the 15th and 16th centuries was mostly limited to high nobility, especially royalty, while lower nobility switched to the use of simple heraldic seals. Early examples (before 1170) Fu...

2016 Formula One motor race 2016 Monaco Grand Prix Race 6 of 21 in the 2016 Formula One World Championship← Previous raceNext race → Layout of the Circuit de Monte Carlo, MonacoRace detailsDate 29 May 2016Official name Formula 1 Grand Prix de Monaco 2016[1][2][3]Location Circuit de MonacoLa Condamine and Monte Carlo, MonacoCourse Street circuitCourse length 3.337 km (2.074 miles)Distance 78 laps, 260.286 km (161.734 miles)Weather Rainy at start,...





