Projectieve ruimte
|
Read other articles:

Javier Mascherano Informasi pribadiNama lengkap Javier Alejandro MascheranoTanggal lahir 8 Juni 1984 (umur 39)Tempat lahir San Lorenzo, Santa Fe, ArgentinaTinggi 1,74 m (5 ft 8+1⁄2 in)[1]Posisi bermain Gelandang BertahanBekKarier senior*Tahun Tim Tampil (Gol)2003–2005 River Plate 46 (1)2005–2006 Corinthians 26 (0)2006–2007 West Ham United 5 (0)2007–2010 Liverpool 94 (2)2010–2018 Barcelona 203 (1)2018–2019 Hebei China Fortune 53 (0)2019–2020 Est...

Jeler totol Acantopsis dialuzona Status konservasiRisiko rendahIUCN181193 TaksonomiKerajaanAnimaliaFilumChordataKelasActinopteriOrdoCypriniformesFamiliCobitidaeGenusAcantopsisSpesiesAcantopsis dialuzona van Hasselt, 1823 Tata namaSinonim takson Acantopsis choirorhynchos (Bleeker, 1854) Cobitis choirorhynchos Bleeker, 1854 lbs Acantopsis dialuzona atau jeler totol adalah ikan jeler yang berasal dari aliran sungai yang deras dan jernih di daratan dan kepulauan Asia Tenggara, dari India hingga I...

The Minute Maid CompanyLogo Minute Maid (2017-sekarang)IndustriMinumanDidirikan1945; 79 tahun lalu (1945) (sebagai Florida Foods, Inc.)KantorpusatSugar Land Town SquareFirst Colony, Sugar Land, Texas, Amerika SerikatTokohkunciJ. Alexander M. Douglas, Jr. (President of North America Group of Coca-Cola)ProdukSari buah, minuman ringanKaryawan1,900[1]IndukThe Coca-Cola CompanySitus webminutemaid.com Minute Maid merupakan lini produk minuman, biasanya berhubungan dengan limun atau jus...

The BreadwinnerTeaser posterSutradaraNora TwomeyProduser Angelina Jolie Jordan Peele Anthony Leo Tomm Moore Andrew Rosen Paul Young Mimi Polk Gitlin Ditulis oleh Anita Doron Deborah Ellis BerdasarkanThe Breadwinneroleh Deborah EllisPemeran Saara Chaudry Soma Bhatia Noorin Gulamgaus Laara Sadiq Ali Badshah Shaista Latif Kawa Ada Ali Kazmi Perusahaanproduksi Cartoon Saloon Aircraft Pictures[1] Guru Studio[2] Jolie Pas[3] Irish Film Board[4] Melusine Productions T...

Beograd Beograd / БеоградIbu kota SerbiaKota Beograd Stari GradBalai Kota, Gereja Santo Sava, Akademi Sains dan Seni Serbia , Benteng Kalemegdan Gedung Majelis Nasional Serbia BenderaLambang kebesaranLetak kota Beograd di Eropa dan SerbiaKoordinat: 44°49′N 20°28′E / 44.817°N 20.467°E / 44.817; 20.467Koordinat: 44°49′N 20°28′E / 44.817°N 20.467°E / 44.817; 20.467Negara SerbiaRegionBeogradMunisipalitas17PendirianSebelum...

British Army officer (1866–1939) Sir George Forestier-WalkerBirth nameGeorge Townshend Forestier WalkerBorn(1866-08-02)2 August 1866Camberley, Surrey, England[1]Died23 January 1939(1939-01-23) (aged 72)Child Okeford, Dorsetshire, EnglandAllegiance United KingdomService/branch British ArmyYears of service1884–1920RankMajor-GeneralUnitRoyal ArtilleryCommands held21st Division27th DivisionBattles/warsSecond Boer WarWorld War IAwardsKnight Grand Cross of the Order ...

Final Piala Champions Eropa 1965Suárez, Facchetti, Peiró dan Bedin dari Inter Milan dengan trofiTurnamenPiala Champions Eropa 1964–1965 Inter Milan Benfica 1 0 Tanggal27 Mei 1965StadionSan Siro, MilanWasitGottfried Dienst (Switzerland)Penonton89,000[1]← 1964 1966 → Final Piala Champions Eropa 1965 adalah pertandingan final Piala Champions Eropa 1964–1965, musim kesepuluh turnamen klub sepak bola utama Eropa yang diselenggarakan oleh UEFA. Itu diperebutkan oleh tim It...
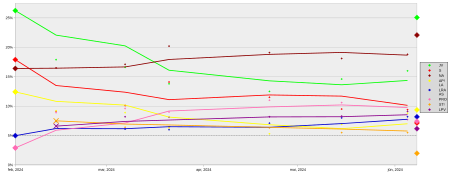
Latvia component of the 2024 European Parliament election 2024 European Parliament election in Latvia ← 2019 8 June 2024 2029 → ← outgoing members9 Latvian seats to the European Parliament Candidate Valdis Dombrovskis Nils Ušakovs Roberts Zīle Party JV Harmony NA Alliance EPP S&D ECR Last election 26.4%, 2 seats 17.6%, 2 seats 16.5%, 2 seats Current seats 3 2 1 Leader Ivars Ijabs Party For Latvia's Development Alliance ALDE Last&#...

Pfastattcomune Pfastatt – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementMulhouse CantoneKingersheim TerritorioCoordinate47°47′N 7°18′E / 47.783333°N 7.3°E47.783333; 7.3 (Pfastatt)Coordinate: 47°47′N 7°18′E / 47.783333°N 7.3°E47.783333; 7.3 (Pfastatt) Superficie5,24 km² Abitanti8 744[1] (2009) Densità1 668,7 ab./km² Altre informazioniCod. postale68120 Fuso orario...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Tirad Pass: The Last Stand of Gen. Gregorio del PilarSutradaraCarlo J. CaparasProduserDonna VillaPemeranRomnick SarmentaPerusahaanproduksiUni-Films Production Inc.DistributorGolden Lion FilmsTanggal rilis 4 Juli 1996 (1996-07-04) NegaraFilipinaBa...

Zailiism在理教 ZàilǐjiàoTypeChinese salvationist religionFounderYang ZaiOrigin17th century TianjinMembers1948: 15 million[1]Other name(s)Liism, Gate of the Principle (理门 Lǐmén), White-Clad Way (白衣道), Octagon Way (八方道)Official websitehttp://www.liism.org/ Part of a series onChinese folk religion Concepts Tian—Shangdi Qi Shen Ling Xian ling Yinyang Hundun Mingyun Yuanfen Baoying Wu Theory Chinese theology Chinese gods and immortals Chinese mythology Chinese cre...

Eparki DohukKatolik Roma (Kaldea) LokasiProvinsi gerejawiBabiloniaMetropolitPatriarkat Babilonia (Kaldea)StatistikPopulasi- Total(per 2013)3.500InformasiDenominasiKatolik Roma (Kaldea)RitusRitus Siria TimurPendirian10 Juni 2013 (2013-06-10) (Penggabungan Keuskupan Amadiyah dan Keuskupan Zaku)KatedralKatedral Mar Aeth Alaha, DuhokKepemimpinan kiniPausFransiskusUskupRabban al Qas Eparki Dohuk adalah sebuah keuskupan Gereja Kaldea pada paruh kedua abad ke-19 dan sebagian besar aba...

Les Essarts-lès-SézannecomuneLes Essarts-lès-Sézanne – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementÉpernay CantoneSézanne-Brie et Champagne TerritorioCoordinate48°45′N 3°39′E / 48.75°N 3.65°E48.75; 3.65 (Les Essarts-lès-Sézanne)Coordinate: 48°45′N 3°39′E / 48.75°N 3.65°E48.75; 3.65 (Les Essarts-lès-Sézanne) Superficie17,38 km² Abitanti280[1] (2009) Densità16,11 ab....

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Quadruple reed – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Bassoon double reeds: note the elliptical (oval) opening (bottom left) Shehnai Cambodian sralai instruments. At left the srali thom (thom me...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

13th quadrennial U.S. presidential election 1836 United States presidential election ← 1832 November 3 – December 7, 1836 1840 → 294 members of the Electoral College148 electoral votes needed to winTurnout56.5%[1] 0.5 pp Nominee Martin Van Buren William Henry Harrison Hugh L. White Party Democratic Whig Whig Alliance Anti-Masonic Home state New York Ohio Tennessee Running mate Richard M. Johnson Francis Granger John Tyler Electoral vote 17...

Эта страница требует существенной переработки. Возможно, её необходимо правильно оформить, дополнить или переписать.Пояснение причин и обсуждение — на странице Википедия:К улучшению/22 июля 2022.Toyota TF103 Категория Формула-1 Разработчик Густав Брюннер Конструктор Panasonic Toyota R...
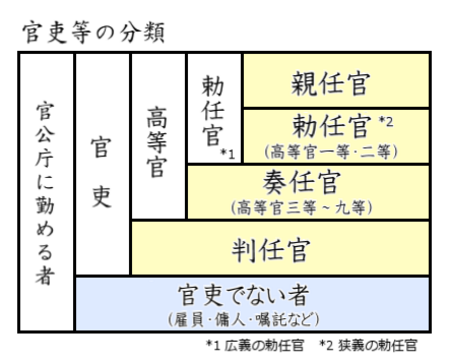
親任官の位置づけ 親任官(しんにんかん)は、1886年(明治19年)に設けられた官吏の分類の一つで[1]、1890年(明治23年)から明治憲法の下で用いられ1948年(昭和23年)に廃止した[2]。官僚制度における最高の位置付けにあり高等官の中の勅任官に含まれた。天皇の親任式を経て任命され、官記には天皇が親署する。親任官と勅任官に対しては、敬称に閣下を...

Concejo Municipal de Aserrí Datos generalesÁmbito Cantón de AserríTipo UnicameralLiderazgoPresidente Sonia Aguilar Zamora (PUSC)desde el 1 de mayo de 2024 Vicepresidente Alexander Antonio Calero López (PLN)desde el 1 de mayo de 2024 ComposiciónMiembros 7 (regidores propietarios) Concejo Municipal de Aserrí (2024-2028).svgGrupos representados 2 PLN 2 ADN 2 PUSC 1 PN...

Beluk Ketupa Status Konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Strigiformes Famili: Strigidae Genus: Ketupa Species: K. ketupu Nama binomial Ketupa ketupu(Horsfield, 1821) Beluk ketupa (Ketupa ketupu), atau juga dikenal sebagai burung hantu ikan Melayu adalah burung hantu ikan dalam keluarga Strigidae. Asli dari Asia Tenggara dan termasuk juga beberapa daerah di Indonesia, mereka terutama hidup di hutan tr...




















![{\displaystyle [x:y:z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/824605c6ea4c4537ff9daf4ce86c26ef6a30f529)

![{\displaystyle [x/z:y/z:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a5352d5eb5e7d4ddf76941b810e2a175f5f002e)
![{\displaystyle [x:y:z]\equiv [x/z:y/z:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/847a95a9e79480ba14e2797f27cabcf1fbdc76c6)
![{\displaystyle [x:y:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f368976b6d23da507c1475db79bbf79887eaa9fc)
![{\displaystyle [x/y:1:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/479b58bbf753659eede9a47f56b30bf55db32bca)
![{\displaystyle [x:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cead9b2f48ec9a9f0c5fd82160ff18222e7c546)


![{\displaystyle [1:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb57ffba69005b439cb1dc8ba40df9c147bae5d2)







