| Bikupolai
|
 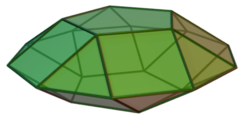
(Pavyzdys: Penkiakampiai bikupolai
orto- ir giro- formos)
|
| Sienos |
2 n-kampiai
2n kvadratų
2n trikampių
|
| Briaunos |
8n
|
| Viršūnės |
4n
|
| Simetrijos grupė |
Orto: Dnh, [2,n], *n22,, eilė 4n
Giro: Dnd, [2+,2n], 2*n, eilė 4n
|
| Sukimo grupė |
Dn, [2,n]+, n22, eilė 2n
|
| Savybės |
iškilas
|
| Kupolai
|

(Pavyzdys: Penkiakampis kupolas)
|
| Tipas |
Kupolai
|
| Schläfli simbolis |
{n} || t{n}
|
| Sienos |
n trikampių,
n kvadratų,
1 n-kampis,
1 2n-kampis
|
| Briaunos |
5n
|
| Viršūnės |
3n
|
| Simetrijos grupė |
Cnv, [1,n], (*nn), eilė 2n
|
| Sukimo grupė |
Cn, [1,n]+, (nn), eilė n
|
| Savybės |
iškilas
|
Geometrijoje kupolas – toks kūnas, kuris susidaro jungiant į briaunainį du daugiakampius, kurių vienas (pagrindas) turi dvigubai daugiau sienų negu kitas, o šiuos daugiakampius sieja lygiašonių trikampių ir stačiakampių juosta. Jei trikampiai yra lygiakraščiai, o stačiakampiai yra kvadratai, o pagrindas ir viršutinis daugiakampis yra taisyklingieji daugiakampiai, tuomet trikampiai, kvadratiniai ir penkiakampiai kupolai yra Džonsono kūnai ir gali būti sudaryti atitinkamai nupjaunant kuboktaedrą, rombinį kuboktaedrą ir rombinį ikosidodekaedrą.
Kupolą galima laikyti prizme, kurios vienas pagrindo daugiakampis buvo sumažintas per pusę, suliejant po dvi gretimas viršūnes.
Kupolą galima žymėti išplėstiniu Schläfli simboliu {n} || t{n}, kuris reiškia taisyklingą daugiakampį {n} sujungtą su lygiagrečiai esančia jo paties nupjautine forma t{n} arba {2n}.
Kupolai yra prizmatoidų poklasis.
Bikupolai
Bikupolas yra geometrinis kūnas, briaunainis, sudarytas iš dviejų kupolų, suglaudus jų pagrindus (didžiuosius daugiakampius).
Bikupolai būna dviejų formų, pagal tai, kaip priglaudžiamas antras kupolas: jei glaudžiasi vienodi pakraščio daugiakampiai (trikampiai prie trikampių ir stačiakampiai prie stačiakampių), tuomet bikupolas yra ortobikupolas (gr. ortho – vietoje); o jei glaudžiasi skirtingi pakraščio daugiakampiai (trikampiai prie stačiakampių), tuomet bikupolas yra girobikupolas (gr. gyro – pasuktas).
Kupolaų ir bikupolų yra be galo daug, kaip ir piramidžių, bipiramidžių, prizmių ir trapecoedrų.
Šešių bikupolų sienos yra taisyklingi daugiakampiai: trikampis (kai viršutinis daugiakampis yra lygiakraštis trikampis), kvadratinis ir penkiakampis (kai viršutinis daugiakampis yra lygiakraštis penkiakampis) – kiekvienas egzistuoja abiejų formų, kaip ortobikupolas ir kaip girobikupolas. Trikampis girobikupolas yra Archimedo kūnas, vadinamas kuboktaedru, o kiti penki yra Džonsono kūnai (J27–J31).
Bikupolai, kurių viršutinis daugiakampis turi daugiau negu 5 lygias kraštines, gali būti sudaromi tik iš lygiašonių trikampių ir stačiakampių, tad jie nebegali būti Džonsono kūnai.
Būdinga bikupolų ypatybė yra ta, kad kiekvienoje jų viršūnėje visada sueina keturi daugiakampiai. Tai reiškia, kad jiems dualūs briaunainiai visada turės keturkampes sienas. Geriausiai žinomas pavyzdys yra rombinis dodekaedras, kurį sudaro 12 rombinių sienų. Ortoformos (trikampio ortobikupolo) dualas taip pat yra dodekaedras, panašus į rombinį dodekaedrą, tik jis turi 6 trapecines sienas, kurių ilgoji ir trumpoji kraštinės keičia viena kitą einant pagal perimetrą.
Šaltiniai
- Norman W. Johnson, „Convex Solids with Regular Faces“, Canadian Journal of Mathematics, 18, 1966, pages 169–200. Čia yra originalus 92 Džonsono kūnų aprašymas.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. Pirmas įrodymas, kad egzistuoja tik 92 Džonsono kūnai.