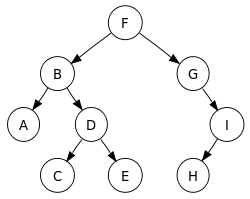
트리 순회
|
Read other articles:

HaggisHaggis yang dijual di pasarBahan utamaJeroan domba (hati, jantung, dan paru-paru) dan lambung sebagai pembungkusnya; bawang merah, oat, suet, rempah-rempahSunting kotak info • L • BBantuan penggunaan templat ini Buku resep: Haggis Media: Haggis Haggis adalah adonan yang terbuat dari jeroan domba yang dicincang bersama dengan bawang merah, oat, suet, rempah-rempah, dan garam, yang dicampur dengan sedikit kaldu, dibungkus dengan lambung domba, lalu direbus dengan t...
Ikon Rusia tentang Pesta Pemuliaan Salib (ikon dari Yaroslavl; karya Gury Nikitin, 1980, Tretyakov Gallery di Moskow). Dalam kalender liturgi Kekristenan, ada beberapa Pesta Pemuliaan Salib Suci yang berbeda, yang mana semuanya memperingati Salib yang digunakan untuk menyalibkan Yesus. Jumat Agung ditujukan untuk mengenang Sengsara dan Penyaliban Kristus, sedangkan Pesta Salib Suci dikhususkan untuk merayakan kayu salib itu sendiri sebagai instrumen keselamatan. 14 September Pesta atau hari r...

Frederick Hamilton-Temple-Blackwood, 1:e markis av Dufferin och Ava Född21 juni 1826[1][2][3]FlorensDöd12 februari 1902[1][2][3] (75 år)Clandeboye House, StorbritannienBegravdBangorMedborgare iFörenade kungariket Storbritannien och IrlandUtbildad vidChrist Church CollegeEton College SysselsättningPolitiker[4], diplomat, författare[5]BefattningLedamot av Brittiska överhusetLedamot av Irlands kronrådLedamot av KronrådetKansler för hertigdömet Lancaster (1868–1872)Kan...

Batalyon Artileri Pertahanan Udara 15/Dahana Bhaladika YudhaLambang Yonarhanud 15/Dahana Bhaladika YudhaDibentuk1 April 1966NegaraIndonesiaCabangArhanudTipe unitSatuan Bantuan TempurPeranPasukan Artileri UdaraBagian dariKodam IV/DiponegoroMarkasSemarang, Jawa TengahJulukanYonarhanud 15/DBYMotoDahana Bhaladika YudhaBaretCoklatMaskotBurung GelatikUlang tahun1 AprilAlutsistameriam S-60 kal 57mm, Dshk 12,7mm dan Rudal RBS-70. Markas Yon Arhanudse 15/Dahana Bhaladika Yudha Batalyon Artileri Pertah...

Questa voce o sezione sull'argomento meteorologia non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Due sole note, i collegamenti esterni sono tutti di servizi/stazioni e inutilizzabili come fonti Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Cumulonembo calvus, nube convettiva in atmosfera La meteorologia[1] (dal greco μετεωρο...

У этого термина существуют и другие значения, см. Съёмка. Съёмка эпизода художественного фильма на натуре Съёмка — процесс создания кинематографического изображения на киноплёнке или цифровом носителе. Киносъёмка является важнейшим этапом кинопроизводства, которы�...

1989 single by Lil LouisFrench KissSingle by Lil Louisfrom the album From the Mind of Lil Louis ReleasedJuly 17, 1989Recorded1989Genre House acid house[1] techno[2][3][4] Length9:52Label FFRR/PolyGram Epic/CBS Songwriter(s) Marvin Burns Karlana Johnson Producer(s)Lil LouisLil Louis singles chronology French Kiss (1989) New York (1989) Alternative coverUS release, B-side French Kiss is a song by American DJ and record producer Lil Louis that became a European a...

1939 film by Walter Lang, William A. Seiter The Little PrincessTheatrical release posterDirected byWalter LangScreenplay byEthel HillWalter FerrisBased onA Little Princess1905 novelby Frances Hodgson BurnettProduced byDarryl F. ZanuckGene MarkeyStarringShirley TempleRichard GreeneAnita LouiseIan HunterArthur TreacherCesar RomeroCinematographyArthur C. MillerWilliam SkallEdited byLouis LoefflerMusic byCharles MaxwellCyril J. MockridgeHerbert W. SpencerSamuel PokrassDistributed byTwentieth Cent...

Disambiguazione – Ostfriesland rimanda qui. Se stai cercando l'omonima nave da guerra, vedi SMS Ostfriesland. Bandiera della Frisia Orientale Mattina in Frisia Mappa della Frisia orientale La Frisia Orientale (in tedesco: Ostfriesland) è una regione costiera del nord ovest dello Stato federato tedesco di Bassa Sassonia. Confina con la Frisia Occidentale (nei Paesi Bassi) e il circondario della Frisia Settentrionale nello stato tedesco dello Schleswig-Holstein; insieme, formano la ...

Dudu Nazionalità Brasile Altezza 166[1] cm Peso 80[1] kg Calcio Ruolo Attaccante Squadra Palmeiras Carriera Giovanili 2005-2010 Cruzeiro Squadre di club1 2009-2010 Cruzeiro6 (0)[2]2010→ Coritiba21 (0)2010-2011 Cruzeiro6 (0)[3]2011-2014 Dinamo Kiev30 (3)2014-2015→ Grêmio35 (3)[4]2015-2020 Palmeiras154 (41)[5]2020-2021→ Al-Duhail22 (14)2021- Palmeiras46 (8) Nazionale 2009-2010 Br...

Disambiguazione – Se stai cercando altri significati, vedi Rio de Janeiro (disambigua). Rio de JaneirocomuneMunicípio do Rio de Janeiro Rio de Janeiro – Veduta LocalizzazioneStato Brasile Stato federato Rio de Janeiro MesoregioneRio de Janeiro MicroregioneRio de Janeiro AmministrazioneSindacoEduardo Paes (PSD) dal 1º gennaio 2021 Data di istituzione1º marzo 1565 TerritorioCoordinate22°54′25″S 43°11′17″W / 22.906944°S 43.188056°W-22.9069...

Vincent Kompany Kompany bermain untuk Belgia pada Piala Dunia FIFA 2018Informasi pribadiNama lengkap Vincent Jean Mpoy Kompany[1]Tanggal lahir 10 April 1986 (umur 38)Tempat lahir Uccle, Brussels, BelgiaTinggi 193 cm (6 ft 4 in)[2]Posisi bermain Bek tengahInformasi klubKlub saat ini Burnley (manajer)Karier junior2000–2003 AnderlechtKarier senior*Tahun Tim Tampil (Gol)2003–2006 Anderlecht 73 (6)2006–2008 Hamburger SV 29 (1)2008–2019 Manchester City 2...

Hairstyling product This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hair wax – news · newspapers · books · scholar · JSTOR (November 2023) (Learn how and when to remove this message) A small tin of hair wax Hair wax is a thick hairstyling product containing wax, used to assist with holding the hair. In contrast with hair gel,...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Campionato olandese di pallanuoto(femminile)Sport Pallanuoto TipoClub Paese Paesi Bassi TitoloCampione dei Paesi Bassi Partecipanti12 (Hkl) StoriaFondazione1901 Detentore Nereus Zaandam Modifica dati su Wikidata · Manuale Il campionato olandese femminile di pallanuoto è l'insieme dei tornei pallanuotistici femminili nazionali per club organizzati dalla Koninklijke Nederlandse Zwembond, la federnuoto dei Paesi Bassi. Quello olandese è il campionato femminile più longevo d'Eu...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...
2020年夏季奥林匹克运动会马来西亚代表團马来西亚国旗IOC編碼MASNOC马来西亚奥林匹克理事会網站olympic.org.my(英文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員30參賽項目10个大项旗手开幕式:李梓嘉和吳柳螢(羽毛球)[1][2]閉幕式:潘德莉拉(跳水)[3]獎牌榜排名第74 金牌 銀牌 銅�...

American college basketball season This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2014–15 Cornell Big Red men's basketball team – news · newspapers · books · scholar · JSTOR (April 2019) (Learn how and when to remove this message) 2014–15 Cornell Big Red men's basketballConferenceIvy LeagueRecord13–17 (5–9 Ivy)Head&#...

بطولة العالم لكرة اليد للرجال 2017تفاصيل المسابقةالبلد المضيف فرنساالتواريخ11–29 يناير 2017الفرق24الأماكن8 (في 8 مدن مضيفة)المراكز النهائيةالبطل فرنساالوصيف النرويجالمركز الثالث سلوفينياالمركز الرابع كرواتياإحصائيات المسابقةالمباريات الملعوبة84الأهداف �...

المسح الجيولوجي الأمريكي (بالإنجليزية: United States Geological Survey) يو اس جي اس—USGS (بالإنجليزية) هيئة المسح الجيولوجي الأمريكية هيئة المسح الجيولوجي الأمريكية تفاصيل الوكالة الحكومية البلد الولايات المتحدة[1] الاسم الكامل الماسح الجيولوجي الأمريكي تأسست 3 مارس ...