오일러의 곱셈 공식
|
Read other articles:

Ada usul agar Brunei Darussalam diganti judulnya dan dipindahkan ke Brunei (Diskusikan). Untuk kegunaan lain, lihat Brunei (disambiguasi). Brunei DarussalamNegara Brunei Darussalam (Melayu)نڬارا بروني دارالسلام (Jawi) Bendera Lambang Semboyan: الدائمون المحسنون بالهدى Sentiasa membuat kebajikan dengan petunjuk Allah (Indonesia: Selalu berbuat baik dengan bimbingan Allah)Lagu kebangsaan: Allah Peliharakan Sultan (Indonesia: Allah Memberka...

System on a chip (SoC) designed by Apple Inc. Apple A8Apple A8 processorGeneral informationLaunchedSeptember 9, 2014DiscontinuedOctober 18, 2022Designed byApple Inc.Common manufacturer(s)TSMC[1][note 1]Product codeAPL1011[2]PerformanceMax. CPU clock rate1.1 GHz (iPod Touch (6th generation)) to 1.4 GHz (iPhone 6, iPhone 6 Plus) and 1.5 GHz (iPad mini 4 & Apple TV (4th Gen))[3] CacheL1 cachePer core: 64 KB instruction + 64 ...

Questa voce o sezione sull'argomento storia del Regno Unito non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Elenco dei re di Bernicia, Deira e Northumbria dopo la migrazione anglosassone prima e vichinga poi. Indice 1 Re anglosassoni di Bernicia 2 Re anglosassoni di Deira 3 Re anglosassoni di Northumbria 4 Re della Northumbria vichinga 5 Sovrani di North...

Russian politician In this name that follows Eastern Slavic naming customs, the patronymic is Zakievich and the family name is Farrakhov. You can help expand this article with text translated from the corresponding article in Russian. (February 2024) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is ac...

此條目可参照英語維基百科相應條目来扩充。 (2022年5月31日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 2022年印第安納州聯邦眾議員選舉 ← 2020 2022年11月8日 2024 → 印第安納州聯邦眾議員全部9個議席...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

This article is about the District. For its eponymous headquarters, see Jamnagar. District of Gujarat in IndiaJamnagar DistrictDistrict of GujaratTop: Lakhota Lake and museum, JamnagarBottom: Mangroves in Pirotan Marine ReserveInteractive Map Outlining Jamnagar DistrictLocation of district in GujaratCoordinates: 22°15′0″N 70°0′0″E / 22.25000°N 70.00000°E / 22.25000; 70.00000Country IndiaStateGujaratRegionSaurashtraHeadquartersJamnagarGovernment �...

Part of the variable chains in immunoglobulins and T cell receptors The upper part (Fab region) of an antibody. The complementarity-determining regions of the heavy chain are shown in red (PDB: 1IGT). Complementarity-determining regions (CDRs) are polypeptide segments of the variable chains in immunoglobulins (antibodies) and T cell receptors, generated by B-cells and T-cells respectively. CDRs are where these molecules bind to their specific antigen and their structure/sequence determ...

Community in the United Kingdom Ethnic group British Cypriots(Cypriots in the United Kingdom)Total populationUK residents born in Cyprus (2011 Census)England: 78,795Wales: 1,215Scotland: 1,941Northern Ireland: 344Regions with significant populationsLondon, Liverpool, Birmingham, Manchester, Glasgow, BristolLanguagesEnglish, Greek, TurkishReligionChristianity, Islam The British Cypriot community in the United Kingdom consists of British people born on, or with ancestors from, the Eastern Medit...

Voce principale: Associazione Calcio ChievoVerona. Associazione Calcio ChievoStagione 1987-1988Sport calcio Squadra Chievo Allenatore Pierluigi Busatta Presidente Bruno Garonzi Serie C2, Gir. B4º Coppa Italia Serie CFase a gironi 1986-1987 1988-1989 Si invita a seguire il modello di voce Questa pagina raccoglie i dati riguardanti l'Associazione Calcio Chievo nelle competizioni ufficiali della stagione 1987-1988. Indice 1 Stagione 2 Rosa 3 Risultati 3.1 Serie C2 3.1.1 Girone di andata 3...

Constituency of Bangladesh's Jatiya Sangsad Barguna-2Constituencyfor the Jatiya SangsadDistrictBarguna DistrictDivisionBarisal DivisionElectorate268,366 (2018)[1]Current constituencyCreated1984PartyAwami LeagueMember(s)Sultana Nadira Barguna-2 is a constituency represented in the Jatiya Sangsad (National Parliament) of Bangladesh since 2024 by Sultana Nadira of the Awami League. Boundaries The constituency encompasses Bamna, Betagi, and Patharghata upazilas.[2][3] Hist...

Assedio di Stepanakertparte della prima guerra del Nagorno KarabakhIl carro armato T-72 restaurato di Gagik Avsharyan per commemorare la cattura di Shusha e la fine dell'assedio di StepankertDatanovembre 1991[1] - 9 maggio 1992[2][3] LuogoStepanakert, Azerbaigian (de jure) Nagorno Karabakh (de facto) EsitoVittoria armena Assedio rimosso dalle forze armene dopo la battaglia di Shushi Schieramenti Nagorno Karabakh (Artsakh)[N 1] Armenia[N 2] Aze...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Naftalena – berita · surat kabar · buku · cendekiawan · JSTOR Naftalena (Bisiklo [4.4.0] deca-1-pentena,3,5,7,9 atau bisiklo [4.4.0] deca-2,4,6,8,10-pentena) merupakan senyawa organik dengan rumus moleku...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Mexico men's national handball team – news · newspapers · books · scholar · JSTOR (March 2024) National handball team MexicoInformationAssociationMexican Handball FederationCoachJulio CamarilloColours 1st 2nd ResultsPan American ChampionshipAppearance...

Restrictions limiting international trade Part of a series onWorld trade Policy Import Export Balance of trade Trade law Trade pact Trade bloc Trade creation Trade diversion Export orientation Import substitution Trade finance Trade facilitation Trade route Domestic trade Tax Restrictions Trade barriers Tariffs Non-tariff barriers Import quotas Tariff-rate quotas Import licenses Customs duties Export subsidies Technical barriers Bribery Exchange rate controls Embargo Safeguards Countervailing...

American textile professional fraternity This article is about the professional fraternity with emphasis on textile arts. For the national social fraternity with a similar nickname, see Phi Kappa Psi. Phi PsiΦΨFoundedMarch 18, 1903; 121 years ago (1903-03-18)Philadelphia College of Textiles & Science, Philadelphia, Pennsylvania, U.S.TypeProfessionalAffiliationIndependentStatusActiveEmphasisTextilesScopeNationalMottoSemper ad perfectumColors Black and GoldF...

日本 > 九州地方 > 福岡県 > 福岡市 > 西区 > 玄界島 玄界島 玄界島の航空写真(2014年)国土交通省 国土地理院 地図・空中写真閲覧サービスの空中写真を基に作成所在地 日本(福岡県福岡市)所在海域 玄界灘座標 北緯33度41分24秒 東経130度14分0秒 / 北緯33.69000度 東経130.23333度 / 33.69000; 130.23333面積 1.16 km²海岸線長 4.4 km最高...

Part of a series on theHistory of the Church of EnglandWestminster Abbey (1749) by Canaletto Middle Ages (597–1500)Anglo-Saxon ChristianityReligion in Medieval EnglandConvocations of Canterbury and YorkDevelopment of dioceses Reformation (1509–1559)Reformation ParliamentDissolution of the MonasteriesThomas CranmerBook of Common Prayer (1549)Edwardine OrdinalsBook of Common Prayer (1552)Forty-two ArticlesMartyrsMarian exiles Elizabethan Church (1558–1603)Book of Common Prayer (1559)Thir...

Questa voce sull'argomento contee del Wisconsin è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di WashburnconteaLocalizzazioneStato Stati Uniti Stato federato Wisconsin AmministrazioneCapoluogoShell Lake Data di istituzione1883 TerritorioCoordinatedel capoluogo45°44′22″N 91°55′32″W45°44′22″N, 91°55′32″W (Contea di Washburn) Superficie2 209 km² Abitanti16 036 (2000) Densità7,26 ab./km² Altre info...
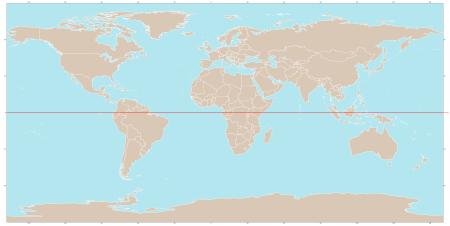
Geographic notion This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Circle of latitude – news · newspapers · books · scholar · JSTOR (April 2012) (Learn how and when to remove this message) Map of Earth Longitude (λ) Lines of longitude appear vertical with varying curvature in this projection, but are actual...






































![{\displaystyle D(n)=\prod _{k=1}^{\infty }\left\{1-\left[1-\prod _{j=1}^{n}\left(1-{{1} \over {p_{k}^{j}}}\right)\right]^{2}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c3cb47c0546b87638881775ea19134ebcc26b2)


