ž†ēžĚė
Ž≥ÄŪėē ž†Ąžóź ž§Ďžč¨ž∂ēžóź žßĀÍįĀžĚīžėÄŽćė ŪŹČŽ©īŪö°Žč®Ž©īžĚÄ Ž≥ÄŪėē ŪõĄžóźŽŹĄ ŪŹČŽ©īžĚĄ žú†žßÄŪēėŽ©į žßĀÍįĀžĚīŽč§.
Ūö°Ūēėž§ĎžĚī žěĎžö©ŪēėŽäĒ Ž≥īŽäĒ ž∂ēŽį©ŪĖ• ÍłłžĚī(x)žóź ŽĒįŽĚľ ž≤ėžßź(w)Í≥ľ ŪöĆž†ĄÍįĀ(őł)žĚī ŽįúžÉĚŪēúŽč§ (Í∑łŽ¶ľ1)
![]() Í∑łŽ¶ľ 1
Í∑łŽ¶ľ 1
Í∑łŽ¶ľ1
Ž≥ÄŪėēžĚī Žß§žöį žěĎžĚÄ(ŽĮłžÜĆŽ≥ÄŪėē)žĚė Í≤Ĺžöį, xŽßĆŪĀľ ŽĖ®žĖīžßĄ ž†źžĚė ŪöĆž†ĄÍįĀžĚÄ tan(őł)žôÄ Í∑ľžā¨ŪēėŽ©į tan(őł)ŽäĒ ž≤ėžßź (ŌČ)žĚė ÍłįžöłÍłį (dŌČ/dx)žôÄ ÍįôŽč§
Ž≤†Ž•īŽąĄžĚī Ž≥ī ÍįÄž†ēžóź ŽĒįŽĚľ, Ž≥ÄŪėēŪõĄ Žč®Ž©ī(ŽĻ®ÍįĄžÉČ žßĀžĄ†)žĚÄ Ž≥ÄŪėē ž†Ą Žč®Ž©ī(ŪĆĆŽěÄžÉČ žßĀžĄ†)žúľŽ°úŽ∂ÄŪĄį dŌČ/dxŽßĆŪĀľ ŪöĆž†ĄŪēúŽč§. (Í∑łŽ¶ľ2žįłÍ≥†) ž∂ēŪēėž§Ď žóÜžĚī Ūö°Ūēėž§Ďžóź žĚėŪēú Ūú®Ž™®Ž©ėŪ䳎ßĆ žěĎžö©ŪēėŽĮÄŽ°ú, ž§Ďžč¨ž∂ēžóźžĄú Ž≥ÄŪėēŽ•†žĚī 0žĚī
ŽźúŽč§.
ž§Ďžč¨ž∂ēžúľŽ°úŽ∂ÄŪĄį yŽßĆŪĀľ ŽĖ®žĖīžßĄ Žč®Ž©ī žúĄžĻėžĚė ž∂ēŽį©ŪĖ• žĄ†Ž≥ÄžúĄŽäĒ tan(őł)žóź yŽ•ľ Í≥ĪŪēėžó¨ ÍĶ¨Ūē†žąė žěąžúľŽ©į, žĚīŽäĒ ŽĮłžÜĆŽ≥ÄŪėēžĚė ÍįÄž†ēžóź žĚėŪēī y*dŌČ/dxžôÄ Í∑ľžā¨ŪēėŽč§.
ž§Ďžč¨ž∂ēžúľŽ°úŽ∂ÄŪĄį yŽßĆŪĀľ ŽĖ®žĖīžßĄ Žč®Ž©ī žúĄžĻėžĚė ž∂ēŽį©ŪĖ• žĄ†Ž≥ÄžúĄŽ•ľ ŽĮłžÜĆÍłłžĚī dxŽ°ú ŽāėŽąĄŽ©ī, ž∂ēŽį©ŪĖ• Ž≥ÄŪėēŽ•†žĚĄ ÍĶ¨Ūē† žąė žěąŽč§. őĶ(y)=d/dx(y*dŌČ/dx)=y(d¬≤ŌČ/dx¬≤)=yőļ őļ=Í≥°Ž•†žĚĄ žĚėŽĮłŪēúŽč§.

Ž©īžĚė ž∂ēŽį©ŪĖ• žĄ†Ž≥ĎŪėēŽ•†žĚÄ yžóź ŽĒįŽĚľ Í≥°Ž•†žóź ŽĻĄŽ°ÄŪēú žßĀžĄ†Ž∂ĄŪŹ¨Ž•ľ ÍįĞߥŽč§
ŪÉĄžĄĪÍĪįŽŹôžĚĄ ŪēėŽäĒ Í≤Ĺžöį Ž≥ÄŪėēŽ•†žóź ŪÉĄžĄĪÍ≥ĄžąėŽ•ľ Í≥ĪŪēėŽ©ī, Žč®Ž©īžĚė Ž≤ēžĄ†žĚĎŽ†•žĚĄ ÍĶ¨Ūē† žąė žěąŽč§.
ŪŹ≠ bžôÄ ŽÜížĚī hŽ•ľ ÍįĖŽäĒ žßĀžā¨ÍįĀŪėē Žč®Ž©īžóź žĚīŽü¨Ūēú Ž≤ēžĄ†žĚĎŽ†•žĚī žěĎžö©ŪēúŽč§Ž©ī, žĚī Ž≤ēžĄ†žĚĎŽ†•žĚī ŽßƎ吏ĖīŽāīŽäĒ Ž™®Ž©ėŪ䳎äĒ Žč®Ž©īŽ™®Ž©ėŪäł MÍ≥ľ ÍįôžēĄžēľ ŪēúŽč§.
ž§Ďžč¨ž∂ēžúľŽ°úŽ∂ÄŪĄį yŽßĆŪĀľ ŽĖ®žĖīžßĄ žßĀžā¨ÍįĀŪėē ŽĮłžÜƎ讎©īžóź žěĎžö©ŪēėŽäĒ Ž≤ēžĄ†žĚĎŽ†•žĚī ŽßĆŽďúŽäĒ ŪěėÍ≥ľ ŪĆĒÍłłžĚī yŽ•ľ Í≥ĪŪēėŽ©ī ŽĮłžÜƎ讎©īžĚė Ž≤ēžĄ†žĚĎŽ†•žĚī ŽßĆŽďúŽäĒ Ūú®Ž™®Ž©ėŪ䳎•ľ Í≥ĄžāįŪē† žąė žěąžúľŽ©į, žĚīŽ•ľ ž†Ąž≤ī ŽÜížĚīžóź ŽĆÄŪēī ž†ĀŽ∂ĄŪēėŽ©ī ž†Ąž≤ī Žč®Ž©īžóź žěĎžö©ŪēėŽäĒ Ž≤ēžĄ†žĚĎŽ†•žĚī ŽßĆŽďúŽäĒ žīĚŪú®Ž™®Ž©ėŪ䳎•ľ žēĄŽěė žčĚÍ≥ľ ÍįôžĚī Í≥ĄžāįŪē† žąė žěąŽč§.
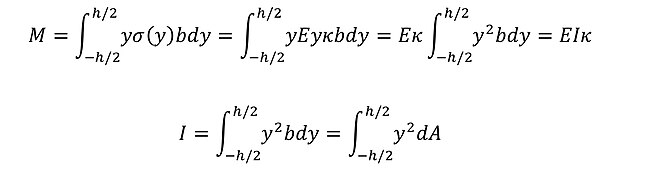
ŪčįŽ™®žĄľžĹĒ Ž≥ī žĚīŽ°† : Ž≥ÄŪėē ž†Ąžóź ž§Ďžč¨ž∂ēžóź žßĀÍįĀžĚīžėÄŽćė ŪŹČŽ©īŪö°Žč®Ž©īžĚÄ Ž≥ÄŪėē ŪõĄžóźŽäĒ ŪŹČŽ©īžĚĄ žú†žßÄŪēėŽ©į ŽćĒ žĚīžÉĀ ž§Ďžč¨ž∂ēžóź žßĀÍįĀžĚīžßÄ žēäŽč§. ž§Ďžč¨ž∂ēÍ≥ľ žā¨žĚīžóź ŽįúžÉĚŪēú ÍįĀ žį®žĚīŽäĒ ž†ĄŽč®Ž≥ĎŪėēŪö®Í≥ľžóź žĚėŪēú Í≤ÉžĚīŽĮÄŽ°ú, ÍĻäžĚÄ Ž≥īžóź ž†Āžö© ŪēúŽč§. Ž≤†Ž•īŽąĄžĚī Ž≥ī žĚīŽ°†Í≥ľŽäĒ ŽįėŽĆÄŽźėŽäĒ žĚīŽ°†žĚīŽč§. Ž≤†Ž•īŽąĄžĚī Ž≥īŽäĒ žĖážĚÄ Ž≥īžóź ž†Āžö©ŪēėŽäĒ žĚīŽ°†žĚīŽč§.