ņäĀĒśĢ ļ│┤Ļ░äļ▓Ģ(ńĘÜÕ×ŗĶŻ£ķ¢ōµ│Ģ, linear interpolation)ņØĆ ļüØņĀÉņØś Ļ░ÆņØ┤ ņŻ╝ņ¢┤ņĪīņØä ļĢī ĻĘĖ ņé¼ņØ┤ņŚÉ ņ£äņ╣śĒĢ£ Ļ░ÆņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņ¦üņäĀ Ļ▒░ļ”¼ņŚÉ ļö░ļØ╝ ņäĀĒśĢņĀüņ£╝ļĪ£ Ļ│äņé░ĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż.
![]() ļæÉ ļ╣©Ļ░äņāē ņĀÉ ņé¼ņØ┤ņŚÉ ņ׳ļŖö Ēīīļ×æņāē ņĀÉņØś ņ£äņ╣śļź╝ ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØä ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż.
ļæÉ ļ╣©Ļ░äņāē ņĀÉ ņé¼ņØ┤ņŚÉ ņ׳ļŖö Ēīīļ×æņāē ņĀÉņØś ņ£äņ╣śļź╝ ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØä ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż.
ņśłņŗ£
ņśłļź╝ ļōżņ¢┤, ņśżļźĖņ¬Į ĻĘĖļ”╝Ļ│╝ Ļ░ÖņØ┤, ļæÉ ļüØņĀÉ  ņÖĆ
ņÖĆ  Ļ░Ć ņŻ╝ņ¢┤ņĀĖ ņ׳ņØä ļĢī, ĻĘĖ ņé¼ņØ┤ņŚÉ ņ£äņ╣śĒĢ£
Ļ░Ć ņŻ╝ņ¢┤ņĀĖ ņ׳ņØä ļĢī, ĻĘĖ ņé¼ņØ┤ņŚÉ ņ£äņ╣śĒĢ£  ņØś Ļ░ÆņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ ļæÉ ņĀÉ ņé¼ņØ┤ņŚÉ ņ¦üņäĀņØä ĻĖŗĻ│Ā ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ╣äļĪĆņŗØņØä ĻĄ¼ņä▒ĒĢĀ ņłś ņ׳ļŗż.
ņØś Ļ░ÆņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ ļæÉ ņĀÉ ņé¼ņØ┤ņŚÉ ņ¦üņäĀņØä ĻĖŗĻ│Ā ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ╣äļĪĆņŗØņØä ĻĄ¼ņä▒ĒĢĀ ņłś ņ׳ļŗż.

ņØ┤ ņłśņŗØņØä ĒÆĆļ®┤, ņ¢┤ļ¢ż ņŻ╝ņ¢┤ņ¦ä Ļ░Æ  ņŚÉ ļīĆĒĢ£
ņŚÉ ļīĆĒĢ£  Ļ░ÆņØä ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĄ¼ĒĢĀ ņłś ņ׳ļŗż.
Ļ░ÆņØä ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĄ¼ĒĢĀ ņłś ņ׳ļŗż.

ņØ╝ļ░śĒÖö
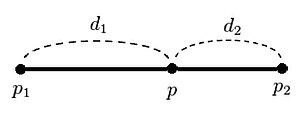 p1Ļ│╝ p2 ņé¼ņØ┤ņŚÉ ņ׳ļŖö ņĀÉ pņØś Ļ░ÆņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØä ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż.
p1Ļ│╝ p2 ņé¼ņØ┤ņŚÉ ņ׳ļŖö ņĀÉ pņØś Ļ░ÆņØä ņČöņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØä ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż.
ņØ╝ļ░śņĀüņ£╝ļĪ£ ļæÉ ņ¦ĆņĀÉ  ņŚÉņä£ņØś ļŹ░ņØ┤Ēä░ Ļ░ÆņØ┤ Ļ░üĻ░ü
ņŚÉņä£ņØś ļŹ░ņØ┤Ēä░ Ļ░ÆņØ┤ Ļ░üĻ░ü  ņØ╝ ļĢī,
ņØ╝ ļĢī,  ņé¼ņØ┤ņØś ņ×äņØśņØś ņ¦ĆņĀÉ
ņé¼ņØ┤ņØś ņ×äņØśņØś ņ¦ĆņĀÉ  ņŚÉņä£ņØś ļŹ░ņØ┤Ēä░ Ļ░Æ
ņŚÉņä£ņØś ļŹ░ņØ┤Ēä░ Ļ░Æ  ļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
ļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.

ļŗ©,  ņØĆ
ņØĆ  ņŚÉņä£
ņŚÉņä£  Ļ╣īņ¦ĆņØś Ļ▒░ļ”¼,
Ļ╣īņ¦ĆņØś Ļ▒░ļ”¼,  ļŖö
ļŖö  ņŚÉņä£
ņŚÉņä£  Ļ╣īņ¦ĆņØś Ļ▒░ļ”¼ļź╝ ļ¦ÉĒĢ£ļŗż.
Ļ╣īņ¦ĆņØś Ļ▒░ļ”¼ļź╝ ļ¦ÉĒĢ£ļŗż.
ļ¦īņØ╝ Ļ▒░ļ”¼ņØś ļ╣äļź╝ ĒĢ®ņØ┤ 1ņØ┤ ļÉśļÅäļĪØ ņĀĢĻĘ£ĒÖöĒĢśļ®┤ ( ) ņ£ä ņŗØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļŗ©ņł£ĒÖöļÉĀ ņłś ņ׳ļŗż.
) ņ£ä ņŗØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ļŗ©ņł£ĒÖöļÉĀ ņłś ņ׳ļŗż.

ĒÖĢņן
ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØĆ 1ņ░©ņøÉ ņ¦üņäĀņāüņŚÉņä£ ņØ┤ļŻ©ņ¢┤ņ¦ĆļŖö ļ│┤Ļ░äļ▓ĢņØ┤ļŗż. ņØ┤ļź╝ 2ņ░©ņøÉņ£╝ļĪ£ ĒÖĢņןĒĢśņŚ¼ ĒÅēļ®┤ņŚÉ ņĀüņÜ®ĒĢ£ Ļ▓āņØ┤ ņØ┤ņżæ ņäĀĒśĢ ļ│┤Ļ░äļ▓Ģ(bilinear interpolation)ņØ┤Ļ│Ā, ņØ┤ļź╝ 3ņ░©ņøÉņ£╝ļĪ£ ĒÖĢņןĒĢśņŚ¼ ņ×ģļ░®ņ▓┤ņŚÉ ņĀüņÜ®ĒĢ£ Ļ▓āņØ┤ ņé╝ņżæ ņäĀĒśĢ ļ│┤Ļ░äļ▓Ģ(trilinear interpolation)ņØ┤ļŗż.
ĒöäļĪ£ĻĘĖļלļ░Ź
ņäĀĒśĢ ļ│┤Ļ░äļ▓ĢņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ░®ļ▓Ģņ£╝ļĪ£ ĒöäļĪ£ĻĘĖļלļ░ŹņØä ĒĢĀ ņłś ņ׳ļŗż.
// p1,p2ļź╝ d1:d2ļĪ£ ļČäĒĢĀĒĢśļŖö pļź╝ ļ”¼Ēä┤ĒĢ£ļŗż. (ļŗ©, d1+d2=1)
float lerp(float p1, float p2, float d1) {
return (1-d1)*p1 + d1*p2;
}
p1, p2ņé¼ņØ┤ņØś ņ×äņØśņØś ņ¦ĆņĀÉ pņŚÉņä£ņØś ļŹ░ņØ┤Ēä░Ļ░Æ f(p)ļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż.

ļö░ļØ╝ņä£, 
Ļ░ÖņØ┤ ļ│┤ĻĖ░
ņÖĖļČĆ ļ¦üĒü¼