서로소 집합 자료 구조
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Karya Mukti, Sungai Melayu Rayak, Ketapang – berita · surat kabar · buku · cendekiawan · JSTOR Karya MuktiDesaNegara IndonesiaProvinsiKalimantan BaratKabupatenKetapangKecamatanSungai Melayu RayakKod...

Kepulauan Solomon padaOlimpiade Musim Panas 2020Kode IOCSOLKONKomite Olimpiade Nasional Kepulauan SolomonSitus webwww.oceaniasport.com/solomonPenampilan pada Olimpiade Musim Panas 2020 di TokyoPeserta3 dalam 3 cabang olahragaPembawa bendera (pembukaan)Sharon FirisuaEdgar IroPembawa bendera (penutupan)Mary Kini LifuMedali 0 0 0 Total 0 Penampilan pada Olimpiade Musim Panas (ringkasan)1984198819921996200020042008201220162020 Kepulauan Solomon berkompetisi di Olimpiade Musim Panas 2020...

Hokkaido Consadole Sapporo北海道コンサドーレ札幌Nama lengkapConsadole SapporoJulukanConsa コンサBerdiri1935 (nama lama Toshiba Horikawa-cho S.C.)StadionSapporo Dome, Sapporo(Kapasitas: 41,484)PemilikHokkaido Football ClubKetuaYoshikadu NonomuraManajerKeiichi Zaizen (2013– )LigaDivisi Satu J. League2023ke-12 Kostum kandang Kostum tandang Hokkaido Consadole Sapporo (北海道コンサドーレ札幌code: ja is deprecated , Hokkaidō Konsadōre Sapporo)[1] adalah klub sep...

Chronologie de la France 1539 1540 1541 1542 1543 1544 1545 1546 1547 ►► Chronologies La flotte de Barberousse hiverne à Toulon.Données clés 1540 1541 1542 1543 1544 1545 1546Décennies :1510 1520 1530 1540 1550 1560 1570Siècles :XIVe XVe XVIe XVIIe XVIIIeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature et Musique classique &...

Tapisserie de BayeuxScène représentant l'évêque Odon de Bayeux tenant un bâton de commandement (baculum), signe d'autorité, lors de la bataille d'Hastings et encourageant les combattants.Artiste InconnuDate Entre 1066 et 1082Commanditaire Odon de BayeuxType Art anglo-saxon, peinture d'histoireTechnique BroderieMatériau toile en lin, broderie Crewel en laineDimensions (H × L) 50 × 6 830 cmPropriétaire État françaisLocalisation BayeuxProtection Mémoire ...

حي الجديدة حي الجديدة في حلب عام 1920 الإحداثيات 36°12′25.0″N 37°09′24.4″E / 36.206944°N 37.156778°E / 36.206944; 37.156778 تقسيم إداري البلد سوريا التقسيم الأعلى حلب تعديل مصدري - تعديل حي الجديدة هو من الأحياء التاريخية في مدينة حلب في سوريا. يعرف الحي بأزقته المتعرجة الضي�...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Vicenza Calcio. Associazione Fascista Calcio VicenzaStagione 1936-1937Sport calcio SquadraVicenza Calcio Allenatore Walter Alt Presidente Giovanni Battista Monti Mario Pittarello Serie C9º posto nel girone A. 1935-1936 1937-1938 Si invita a seguire il modello di voce...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Town in Connecticut, United StatesNewington, ConnecticutTownTown of NewingtonMain Street Seal Hartford County and Connecticut Capitol Planning Region and ConnecticutShow NewingtonShow ConnecticutShow the United StatesCoordinates: 41°41′14″N 72°43′48″W / 41.68722°N 72.73000°W / 41.68722; -72.73000Country United StatesU.S. state ConnecticutCountyHartfordRegionCapitol RegionIncorporated1871Government • TypeCouncil-manager ...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Religious affiliation in th...

خريطة لجميع الإحداثيات من جوجل خريطة لجميع الإحداثيات من بينغ تصدير جميع الإحداثيات من كيه إم إل تصدير جميع الإحداثيات من جيو ر س س خريطة لجميع الإحداثيات الميكرو منسقة بيانات من إطار توصيف الموارد هذه القائمة غير مكتملة. فضلاً ساهم في تطويرها بإضافة مزيد من المعلومات ولا...

Carpenter of Pinocchio For other uses, see Geppetto (disambiguation). Fictional character GeppettoThe Adventures of Pinocchio characterGeppetto carving Pinocchio.First appearanceThe Adventures of Pinocchio (1883)Created byCarlo CollodiIn-universe informationSpeciesHumanGenderMaleOccupationCarpenterFamilyPinocchio (son)NationalityItalian Geppetto (/dʒəˈpɛtoʊ/ jə-PET-oh Italian: [dʒepˈpetto])[1] is an Italian fictional character in the 1883 novel The Adventures of Pinocc...

Italian alpine skier Roberta MelesiMelesi in 2023Personal informationBorn (1996-07-18) 18 July 1996 (age 27)Lecco, ItalyOccupationAlpine skierSkiing careerDisciplinesSpeed eventsClubG.S. Fiamme OroWorld Cup debut2017World CupSeasons7 Roberta Melesi (born 18 July 1996) is an Italian alpine skier.[1] Career During her career she has achieved two results among the top 15 in the FIS Alpine Ski World Cup.[1] World Cup results Top 15 Date Place Discipline Rank 26-11-2022 Killin...

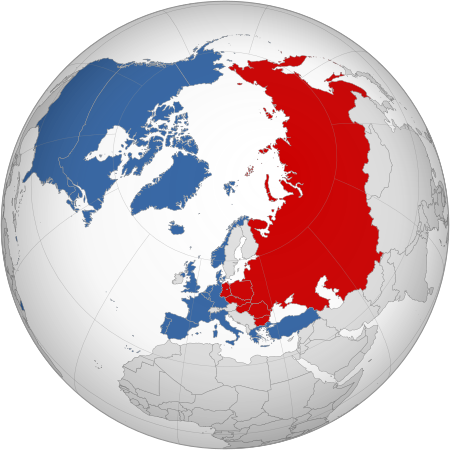
Reactions to the 2021–2022 Russo-Ukrainian war Further information: Government and intergovernmental reactions to the Russian invasion of Ukraine and Non-government reactions to the Russian invasion of Ukraine Main article: Prelude to the Russian invasion of Ukraine This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (November 2023) vteRusso-Ukrainia...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Cet article est une ébauche concernant une localité roumaine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Valea lui MihaiNom officiel (ro) Valea lui MihaiNoms locaux (ro) Valea lui Mihai, (hu) ÉrmihályfalvaGéographiePays RoumanieRégions Région de développement Nord-VestJudeț BihorChef-lieu Valea lui Mihai (d)Superficie 73,54 km2Altitude 127 mCoordonnées 47° 31′ 12�...

This article is part of a series on theHistory of Australia Timeline and periods Prehistory European exploration (sea) European exploration (land) 1788–1850 1851–1900 1901–1945 1945–present Topics Abortion Agriculture Antisemitism Anzac Day Banking Capital punishment Civil rights Cinema Constitution Diplomacy Economics Eureka Rebellion Federation 1901 Federal Flag Design Competition Historiography Immigration Labour LGBT Military Monarchy Sports Telecommunications Rail transport Reli...
Enlèvement de Kim Dae-jung Le Palace Hotel où a lieu la tentative d'enlèvement. Type enlèvement d'opposant politique Pays Japon Localisation Tokyo Coordonnées 35° 41′ 05″ nord, 139° 45′ 41″ est Date 8 août 1973 Participant(s) KCIA Géolocalisation sur la carte : Tokyo Géolocalisation sur la carte : Japon modifier L'enlèvement de Kim Dae-jung, principal opposant à la dictature sud-coréenne de Park Chung-hee, qui venait de réfo...

Citizens and nationals of India For other uses, see Indian (disambiguation). Ethnic group IndiansFlag of India Countries with a significant population with Indian ancestry. India + 1,000,000 + 100,000 + 10,000 + 1,000 No dataTotal populationc. 1.4 billionRegions with significant populationsIndian diaspora:c. 32,285,425 (2023 estimate, including people of Indian origin)[1] United States4,946,306[2&#...
Novel by Douglas Preston and Lincoln Child This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Reliquary novel – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this message) Reliquary AuthorDouglas Preston,Lincoln ChildLanguageEnglishSeriesAloysius PendergastGenreThril...














